데이터 취업 스쿨 교육 6회차 내용 정리

6. 수열

3)-1 등비수열

• 연속된 두항의 비(r)가 일정한 수열
• 등비중항
  - 연속된 세항에서 가운데 항
• n번째 값 : an = a1 * r**(n - 1)
• a1부터 an까지의 합 : sn = a1 * (1-(r**n))/(1-r)을 이용한 구현

3)-2 파이썬으로 등비수열 표현

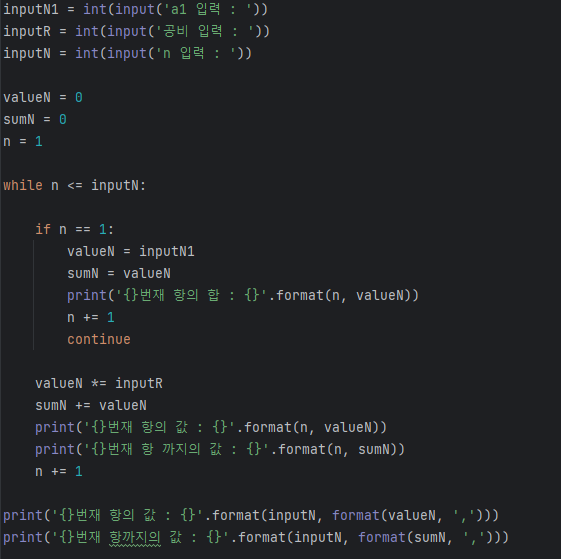• while 문을 이용한 구현
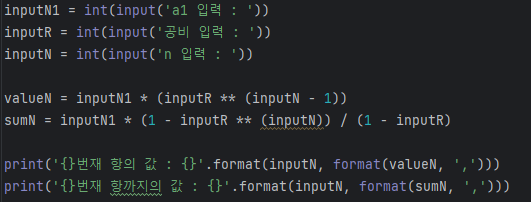• an = a1 r**(n - 1)과 sn = a1 (1-(r**n))/(1-r)을 이용한 구현

7. 시그마

1) 개념

• Σ란, 수열의 합을 나타내는 기호

2) 등차수열

-등차수열의 합
- an = a1+(n-1)d
- sn = n*(a1 + an)/2

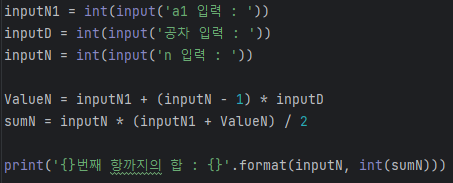공식을 이용해 파이썬에서 구현

3) 등비수열

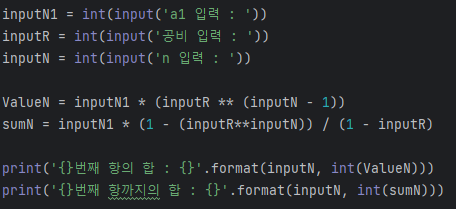
-등비수열의 합
- an = a1 (r ** (n-1))
- sn = a1 (1 - r**n) / (1 - r)

8. 계차수열

1) 개념

• 어떤 수열의 인접하는 두 항의 차로 이루어진 또 다른 수열

2) 계차수열을 이용해 수열 an의 일반항 도출

3) 파이썬을 이용한 계차수열

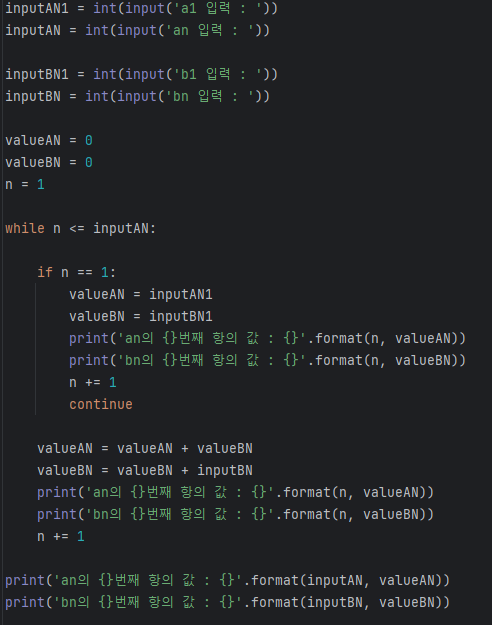
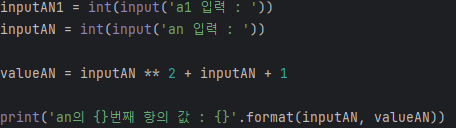
• an의 일반항을 구할 수 있을 때는 위와 같이도 구현 가능.

9. 피보나치 수열

1) 개념

• 세 번째 항은 두 번째항과 첫 번째 항을 더한 합이다.

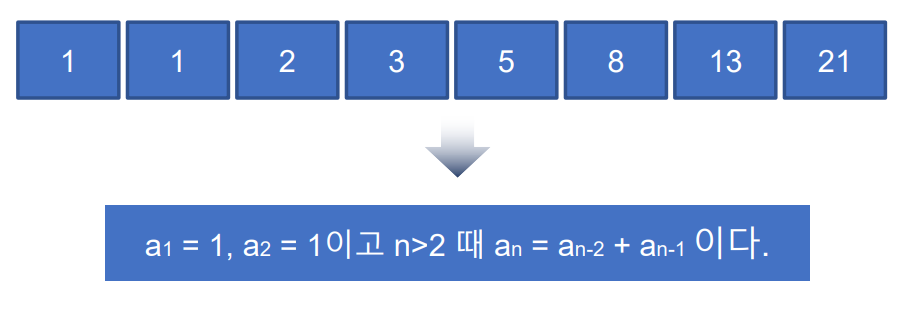
2) 파이썬을 이용한 피보나치 수열

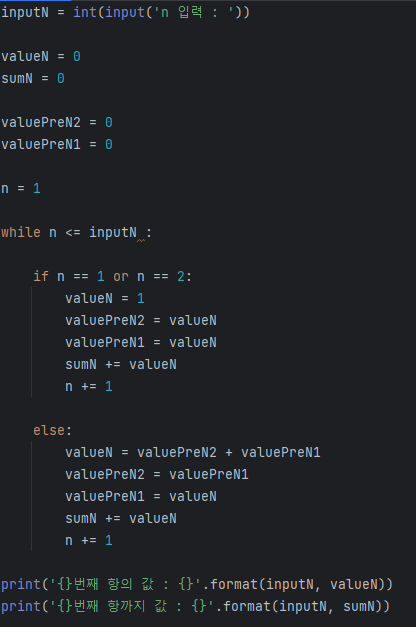
10. 팩토리얼

1) 개념

• 1부터 야의 정수 n까지의 정수를 모두 곱한 것
• 0!은 1이다.

2) 파이썬을 이용한 팩토리얼

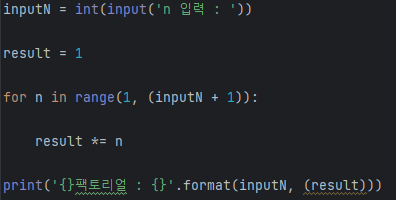• 코드를 입력하는 경우
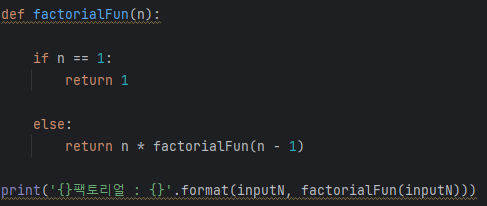• 함수를 선언하는 경우
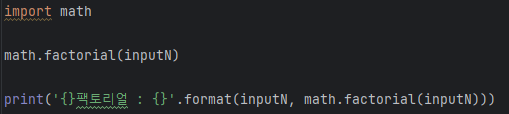• 모듈을 사용하는 경우

11. 군수열

1) 개념

• 여러개의 항을 묶었을 때 규칙성을 가지는 수열
  

2) 파이썬을 이용한 군수열

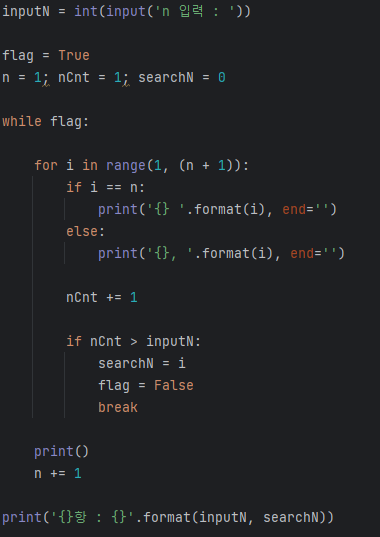
12. 순열

1) 개념

• n개에서 r개를 택하여 나열하는 경우의 수
• nPr로 표현하며 아래와 같은 공식으로 구할 수 있음.
  - n(n-1)(n-2)...(n-r+1)
  - n!/(n-r)!
  - 단, 0<r<=n

2) 파이썬을 이용한 순열

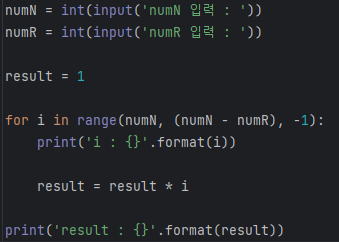
3) 원순열

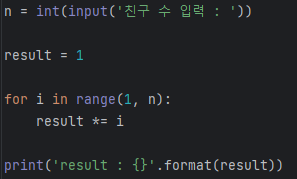
• 시작과 끝의 구분이 없는 순열
• n!/n 또는 (n-1)!로 구할 수 있음.

13. 조합

1) 개념

• n개에서 r개를 택하는 경우의 수
• 순열과 조합의 다른 점은 순서와 상관 없다는 것.
• nCr = n!/(r!(n-r)!)

2) 파이썬을 이용한 조합

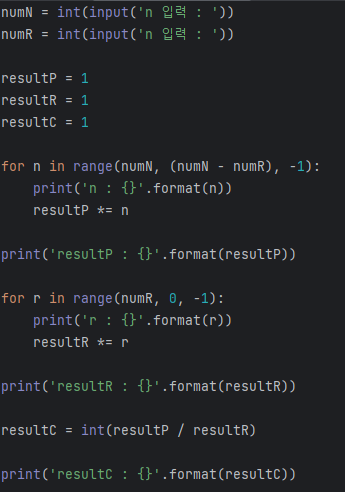• nCr = nPr/r! 을 이용하여 구현

14. 확률

1) 개념

• 모든 사건에서 특정 사건이 일어날 수 있는 수를 나타낸 것.
• 이중 모든 사건을 '표본 공간' / 특정 사건을 '사건'이라고 함.

2) 확률과 조합

3) 파이썬을 이용한 확률과 조합

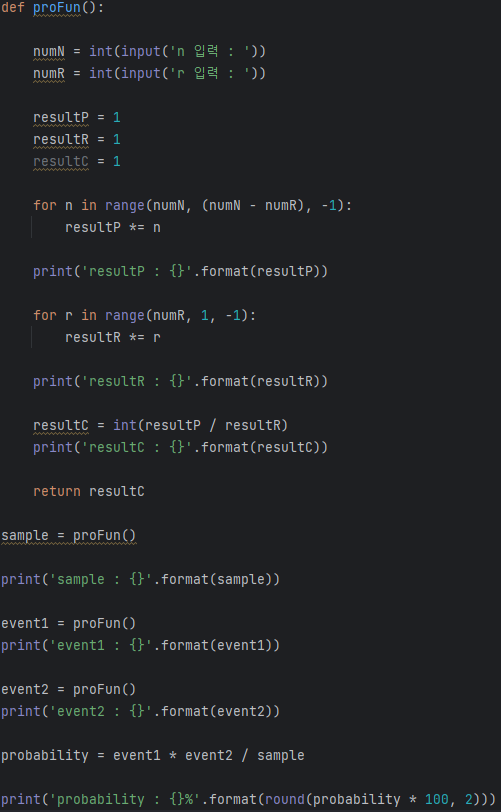• nCr = nPr/r!과 for문을 이용하여 구현