알고리즘 - A* 알고리즘

📒 A* 알고리즘

📌 A* 알고리즘이란?

• 다익스트라 알고리즘을 확장하여 만들어진 경로 탐색 알고리즘
• 주로 게임에서 플레이어를 목표 지점으로 이동시킬 때 사용한다.
• 시작 노드와 목적지 노드를 분명하게 지정하여 이 두 노드 간의 최단 경로를 파악하는 알고리즘
• 휴리스틱 추정값을 통해 알고리즘을 개선할 수 있다.
• 이러한 휴리스틱 추정값을 어떤 방식으로 제공하느냐에 따라 얼마나 빨리 최단 경로를 파악할 수 있느냐가 결정된다.
  
  

📌 A* 알고리즘이 필요한 이유

• 다익스트라를 직접 현실 문제에 적용하기가 매우 부담되었다. 당장에 네트워크 같은 디지털적인 공간이 아닌, 현실의 사람이 사는 공간을 생각해 보자. 사람이 다닐 수 있는 "거리는" 명백히 아날로그다. 이것들을 전부 노드화 시키기에는 그 수가 엄청나게 많아질 수 있다. 그렇다면 탐색해야 하는 공간도 그만큼 커지게 되고, 시간 복잡도 역시 매우 커질 것이다.
• 또한, 잘 노드화 시켜서 다익스트라를 사용할 수 있는 상황을 만들어 경로를 발견했다 하더라도, 탐색한 경로가 자동차 정체 구간, 출근길 등 다양한 변수로 인해 오히려 더 느려질 수 있는 경우도 발생하기 마련이다.
• 이러한 변수 때문에 A* 알고리즘을 사용하는 것이다.
  
  

📌 BFS / 다익스트라 / A*의 차이점

• BFS : 가중치가 없는 그래프에서 최단 경로를 찾는 완전 탐색 알고리즘
• 다익스트라 : 가중치 그래프에서 시작 노드를 기준으로 모든 노드까지의 최단 거리를 구하는 그리디 알고리즘
• A* : 가중치 그래프에서 시작 노드에서 목표 노드까지의 최단 경로만을 구하는 그리디 알고리즘
  
  

📌 A* 알고리즘 개념

열린 목록(Open List) : 현재 조사하고 있는 노드에 인접한 리스트로, 최단 거리로써 선택 가능성이 열려있는 노드들의 집합
닫힌 목록(Closed List) : 조사가 끝난 노드들의 집합(다시 조사할 필요가 없는 집합)
g(x) : 현재 상태의 비용
h(x) : 현재 상태에서 다음 상태로 이동할 때의 휴리스틱 함수
f(x) = g(x) + h(x)
휴리스틱 함수 : 현재 노드에서 목표 노드까지의 예상 비용을 구하는 함수 h(n)
대표적인 휴리스틱 함수 : 맨해튼 거리 함수, 유클리디안 거리 함수

• 가장 최소 비용으로 도달한 지점부터 탐색하는 다익스트라 알고리즘의 원리를 차용한 것으로, A* 알고리즘은 현재 상태의 비용을 g(x), 현재 상태에서 다음 상태로 이동할 때의 휴리스틱 함수를 h(x)라고 할 때, 둘을 더한 f(x) = g(x) + h(x)가 최소가 되는 지점을 우선 적으로 탐색하는 방법이다.
• 이 f(x)가 작은 값부터 탐색하는 특성상 우선순위 큐가 사용된다.
• 휴리스틱 함수 h(x)에 따라 성능이 극명하게 갈리며, f(X) = g(x)일 때는 다익스트라 알고리즘과 동일하다.
• 또한, 현명하게 사용하지 못하면 상당한 메모리와 시간을 소모하게 된다.
  
  

📌 A* 알고리즘의 기본 동작

1. f(x)를 오름차순 우선순위 큐에 노드로 삽입한다.
2. 우선순위 큐에서 최우선 노드를 pop 한다.
3. 해당 노드에서 이동할 수 있는 노드를 찾는다.
4. 그 노드들의 f(x)를 구한다.
5. 그 노드들을 우선순위 큐에 삽입한다.
6. 목표 노드에 도달할 때까지 반복한다.
   
   

📌 A* 알고리즘 예시

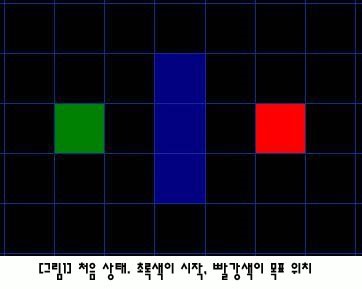
• 위 그림과 같이 장애물이 있는 맵에서 A* 알고리즘을 사용하여 목표까지의 가장 짧은 경로를 찾는 예를 살펴보자.
• 초록색은 시작 위치, 빨간색은 목표 위치, 파란색은 장애물로써 지나갈 수 없는 위치이다.
  
  
  

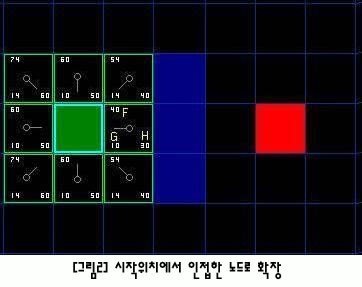
• 처음 시작 위치에서 이웃 노드들로 확장하며 노드마다 f(x) 값을 계산한다.
• 각 이웃 노드 가운데의 그림은 이전 상태 노드를 가리키는 것으로, 직선 방향의 상태가 바로 이전의 지나왔던 상태이다.
• 상태마다 이전 상태의 위치 정보도 저장하고 있어야 한다.
  
  
  

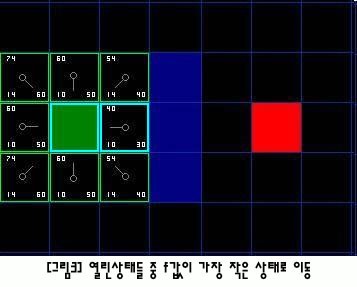
• 열린 상태(이웃 노드이자 그림에서는 녹색 테두리를 가진 사각형들) 중, f(x) 값이 가장 작은 상태로 이동한다.
  
  
  

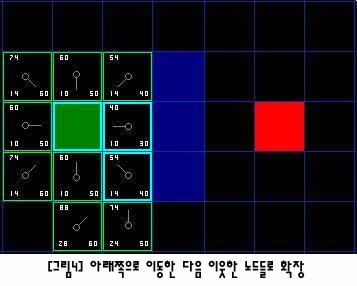
• 다음 이동에서는 아래 노드나 위 노드나 f(x)의 값이 같으므로 어느쪽을 선택해도 상관없지만, 그림에서는 밑으로 이동하였다.
• 그런 다음, 인접한 노드들의 f(x) 값을 계산한다. 시작 노드와 현재의 바로 위 노드, 현재의 왼쪽 노드는 이미 열린 상태에 있으므로 값이 바뀌었는지만 살펴보고, 밑의 두 노드는 새로운 노드이므로 f(x) 값을 계산한 후 열린 상태에 넣는다.
  
  
  

• 이런 방식으로 f(x) 값이 가장 작은 노드들로 계속 확장해 나간다.
• 그림에서 파란색 테두리는 닫힌 상태를 가리키는 것으로, 이미 지나왔던 노드들을 의미한다.
  
  
  

• 목표 상태에 도달한 다음에는 상태마다 저장되어 있는 이전 상태의 경로를 따라, 시작 위치부터 목표 위치까지의 경로를 구한다.
• 이 경로가 목표까지의 가장 짧은 경로가 되고, 알고리즘을 종료한다.

출처 : http://aidev.co.kr/game/501