📒 갈무리 - 트리(Tree)
📌 비선형 자료구조란?
- 자료의 순서가 불규칙하고 자료 간의 연결이 여러 줄로 연결된 자료구조
- 하나의 자료 뒤에 여러 개의 자료가 존재할 수 있다.
ex) 관계도, 지하철 노선도, 도로망 등 계층적 구조
📌 트리란?
- 노드(Node)로 이루어진 자료구조
- 하나의 루트 노드를 갖는다.
- 루트 노드는 0개 이상의 자식 노드를 갖고 있다.
- 그 자식 노드 또한 0개 이상의 자식 노드를 갖고 있고, 이는 반복적으로 정의된다.
- 모든 자식 노드는 한 개의 부모 노드만을 갖는다.
- 각 노드는 어떠한 자료형으로도 표현이 가능하다.
📌 트리와 관련된 용어
루트 노드(Root Node) : 부모가 없는 노드
리프 노드(Leaf Node) : 자식이 없는 노드이며 '단말 노드'라고도 한다.
형제 : 같은 부모를 갖는 노드
간선(Edge) : 노드들을 연결하는 선이라 하며 'Link'또는 'branch'라고도 한다.
노드의 깊이(Depth) : 루트 노드에서 어떤 노드에 도달하기 위해 거처야 하는 간선의 수
노드의 레벨(Level) : 트리의 특정 깊이를 가지는 노드의 집합(루트 노드가 레벨 0)
노드의 차수(Degree) : 하위 트리 개수 / 간선 수 = 각 노드가 지닌 가지의 수
트리의 높이(Height) : 루트 노드에서 가장 깊숙이 있는 노드의 깊이
📌 트리의 특징
- 그래프의 한 종류이다.
- 아래로만 갈 수 있는 그래프 종류 중 하나이다.
- 계층 모델이다.
- DAN의 한 종류이다.
DAN(Directed Acycle Graphs) : 방향성이 있는 비순환 그래프
- 노드가 N개인 트리는 N-1개의 간선(Edge)을 갖는다.
- 임의의 노드에서 어떤 노드로 가는 경로는 유일하다. (사이클이 없기 때문)
- 한 개의 루트 노드만이 존재하고, 모든 자식 노드는 한 개의 부모 노드만을 갖는다.
- 부모 자식 관계이기 때문에 흐름은 Top->Bottom 또는 Bottom -> Top으로 이루어 진다.
- 순회(Traversal)는 Pre-order(전위), In-order(중위) 또는 Post-order(후위)로 이루어진다. 이 3가지 모두 깊이 우선 탐색(DFS)과 넓이 우선 탐색(BFS) 안에 있다.
- 트리의 종류는 이진 트리, 이진 탐색 트리, 균형 트리, 이진 힙등이 있다.
📌 이진 트리(Binary Tree)
- 컴퓨터에서 사용되는 데이터 구조의 하나로, 루트가 있는 트리 구조에서 각 노드의 자식의 수가 최대 2개를 넘지 않는 트리이다.
📌 이진 트리의 종류
포화 이진 트리 : 모든 레벨의 노드가 꽉 차있고, 단말 노드를 제외한 모든 노드의 차수가 이진 트리의 형식인 이진 트리
완전 이진 트리 : 왼쪽부터 모두 채워진 이진 트리
높이 균형 트리 : 모든 단말 노드의 깊이 차이가 최대 1인 이진 트리
완전 높이 균형 트리 : 왼쪽 하위 트리와 오른쪽 하위 트리의 깊이가 같은 이진 트리
📌 이진 트리의 순회(Traversal)
- 이진 트리의 모든 노드를 특정한 순서대로 한 번씩 방문하는 것
📌 전위 순회
- 루트 노드에서 시작하여 항상 왼쪽 자식 노드를 우선 적으로 방문하는 순회
루트 노드 -> 왼쪽 서브 트리 -> 오른쪽 서브 트리
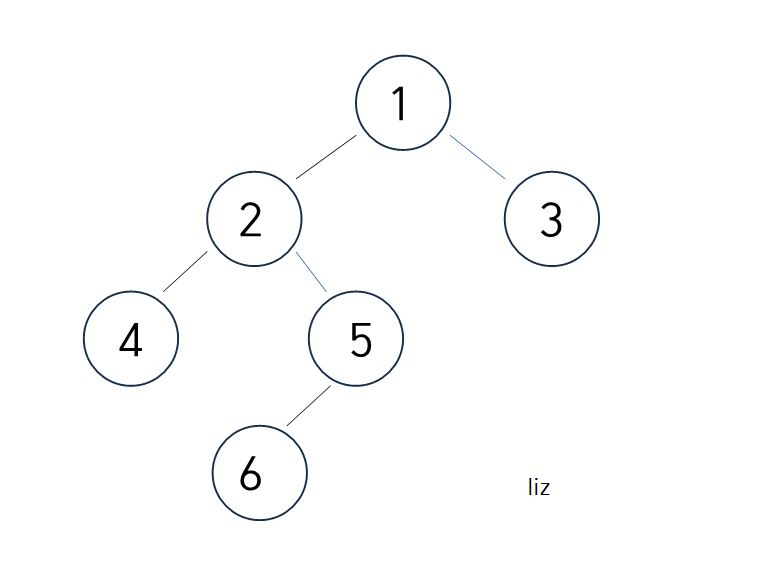
위 사진을 순회한다면,
1 -> 2 -> 4 -> 5 -> 6 -> 3
📌 중위 순회
- 루트 노드를 먼저 방문하지 않고 왼쪽 서브 트리부터 방문하여 루트 노드가 중간에 방문되는 순회
왼쪽 서브 트리 -> 루트 노드 -> 오른쪽 서브 트리
위 사진을 순회한다면,
4 -> 2 -> 5 -> 6 -> 1 -> 3
📌 후위 순회
- 왼쪽 서브 트리와 오른쪽 서브 트리를 우선적으로 방문한 후 가장 마지막으로 루트 노드를 방문하는 순회
왼쪽 서브 트리 -> 오른쪽 서브 트리 -> 루트 노드
위 사진을 순회한다면,
4 -> 6 -> 5 -> 2 -> 3 -> 1
📌 이진 트리 DFS, BFS
- 이진 트리의 순회는 전위, 중위, 아니면, 후위 순회로 이루어지고 3가지 모두 DFS(깊이 우선 탐색)와 BFS(넓이 우선 탐색)안에 있다.
- DFS가 BFS보다 좀 더 간단하다.
- 속도는 DFS가 BFS보다 느리다.
📌 DFS(Depth-First-Search)
- 최대한 깊이 내려간 뒤, 더 이상 갈 곳이 없을 경우 옆으로 이동
위 사진을 깊이 우선 탐색한다면,
1 -> 2 -> 4 -> 5 -> 6 -> 3
- 스택 또는 재귀 호출로 구현
- 검색 대상 그래프가 크다면 DFS를 고려
📌 BFS(Breath First Search)
- 왼쪽부터 최대한 넓게 이동한 후, 더 이상 갈 수 없을 때 아래로 이동
위 사진을 넓이 우선 탐색한다면,
1 -> 2 -> 3 -> 4 -> 5 -> 6
- 큐를 이용해서 구현
- 최단 경로를 찾아야 할 경우에 사용
- 검색 대상의 규모가 크지 않고, 검색 시작 지점으로부터 원하는 대상이 멀지 않다면 BFS를 고려