한수는 크기가 2^N × 2^N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다.

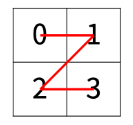
N > 1인 경우, 배열을 크기가 2^(N-1) × 2^(N-1)로 4등분 한 후에 재귀적으로 순서대로 방문한다.

다음 예는 2^2 × 2^2 크기의 배열을 방문한 순서이다.

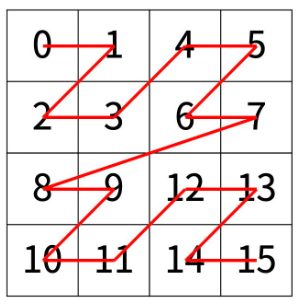
N이 주어졌을 때, r행 c열을 몇 번째로 방문하는지 출력하는 프로그램을 작성하시오.

다음은 N=3일 때의 예이다.

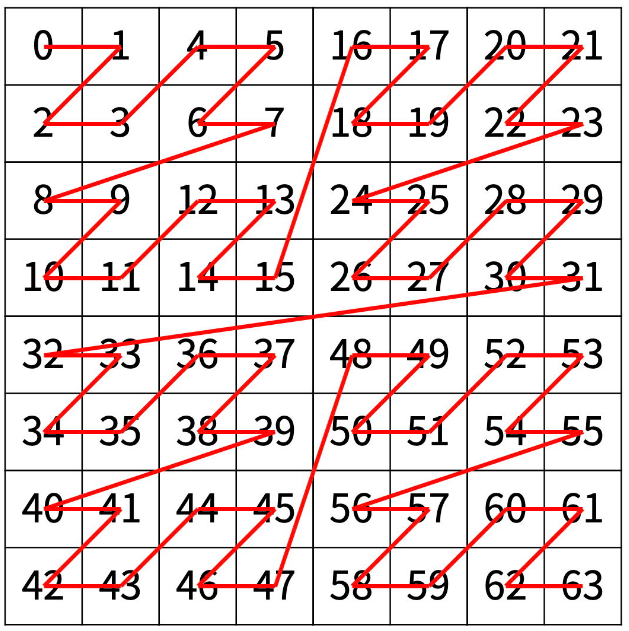
🔎 문제 파악

quadtree 문제(Baekjoon_2630)처럼 2의 N승 크기의 정사각형 배열을 좌상단, 우상단, 좌하단, 우하단으로 4등분하여 순차적으로 탐색하도록 한다.

입력으로 배열의 크기(N), 행(r)과 열(c)을 받고 주어진 행과 열에 대응되는 장소가 몇 번째로 방문되어지는 지를 계산해야 한다.

N이 2일 때의 예시를 확인해보자.
길이가 4인 전체 배열을 4등분한다면 길이가 2인 배열 4개가 나온다. 이 때 좌상단 배열은 시작값이 0, 끝값이 2^2-1이다. 끝값에 주목하길 바란다.

💡 만약 입력받은 행과 열이 우상단 배열에 존재한다면, 좌상단을 다시 탐색하면서 거칠 필요가 없고 그저 "진행된 탐색의 횟수"를 (좌상단 배열의 끝값 + 1)로 잡은 후 분할&정복을 이용하여 다시 계산한다.

🔑 Divide and Conquer

문제를 푸는 핵심은 divide and conquer에 있음을 기억하며 기본적인 틀부터 잡아보겠다.

def quadSegment(length: int, r: int, c: int):
	global cnt
	
    if 좌상단:
		quadSegment(half_len, r, c)
        
	# 분할 과정에서 행과 열 값이 바뀌니 다시 계산한다.
	elif 우상단:
		quadSegment(half_len, r, c') 

	elif 좌하단:
		quadSegment(half_len, r', c)

	elif 우하단:
		quadSegment(half_len, r', c')

입력 받은 행과 열에 대응되는 장소가 좌상단에 위치하고 있다면 시작값과 행, 열 값을 바꾸지 않고 재분할한다.

우상단에 위치한 장소는 cnt를 (좌상단 끝값 + 1)만큼 늘려주고 재분할하여 새로이 생긴 배열의 행, 열 정보로 수정하여 quadSegment함수에 집어 넣는다.

좌하단과 우하단도 같은 원리로 동작하도록 구현한다.

def quadSegment(length: int, r: int, c: int):
	global cnt
	half_len = length // 2

	if r < half_len and c < half_len:
		if half_len == 1:
			return
		quadSegmentation(half_len, r, c)

	elif r < half_len and c >= half_len:
		if half_len == 1:
			cnt += 1
			return

		cnt += pow(half_len, 2)
		quadSegmentation(half_len, r, c - half_len)

	elif r >= half_len and c < half_len:
		if half_len == 1:
			cnt += 2
			return

		cnt += pow(half_len, 2) * 2
		quadSegmentation(half_len, r - half_len, c)

	elif r >= half_len and c >= half_len:
		if half_len == 1:
			cnt += 3
			return

		cnt += pow(half_len, 2) * 3
		quadSegmentation(half_len, r - half_len, c - half_len)

🚀최종 코드

최종 코드는 다음과 같다.

def quadSegment(length: int, r: int, c: int):
	global cnt
	half_len = length // 2

	if r < half_len and c < half_len:
		if half_len == 1:
			return
		quadSegmentation(half_len, r, c)

	elif r < half_len and c >= half_len:
		if half_len == 1:
			cnt += 1
			return

		cnt += pow(half_len, 2)
		quadSegmentation(half_len, r, c - half_len)

	elif r >= half_len and c < half_len:
		if half_len == 1:
			cnt += 2
			return

		cnt += pow(half_len, 2) * 2
		quadSegmentation(half_len, r - half_len, c)

	elif r >= half_len and c >= half_len:
		if half_len == 1:
			cnt += 3
			return

		cnt += pow(half_len, 2) * 3
		quadSegmentation(half_len, r - half_len, c - half_len)
        
N, r, c = map(int, input().split())
cnt = 0
length = pow(2, N)
quadSegmentation(length, r, c)
print(cnt)