학교에서 제공하는 여름방학 코딩 테스트 대비 캠프 with 코드트리 | 코딩테스트 준비를 위한 알고리즘 정석에 수록된 문제 풀이 및 강의 정리 내용입니다.
구현 in Coding Test
코딩 테스트에서 구현이란 생각을 코드로 바꾸는 과정을 의미한다. 최근 삼성에서 자주 출제 되고 있는 코테 유형 중 하나인 시뮬레이션은 구현 카테고리 중 하나이다. 구현 문제들은 손과 눈으로 문제를 따라가면 풀이는 간단하지만 막상 코드를 짜려고 하면 어려워 지는 경우가 많다. 구현 문제의 대표적인 예는 완전 탐색과 시뮬레이션이 있다.
완전 탐색(Brute-Force)
완전 탐색이란 문제를 해결할 때 될 수 있는 모든 경우를 고려하여 정답을 찾는 걸 의미한다. 예를 들어 n개의 숫자 중 m 개의 숫자를 적절히 골라 합이 최대가 되도록 해야 한다면, 두 숫자의 합이 될 수 있는 모든 경우의 수 중 최대 값을 찾게 되는데 이를 완전탐색이라 부른다. 일반적으로 for문을 사용한 완전탐색과 재귀를 사용한 완전 탐색이 존재한다.
격자 안에서 완전 탐색
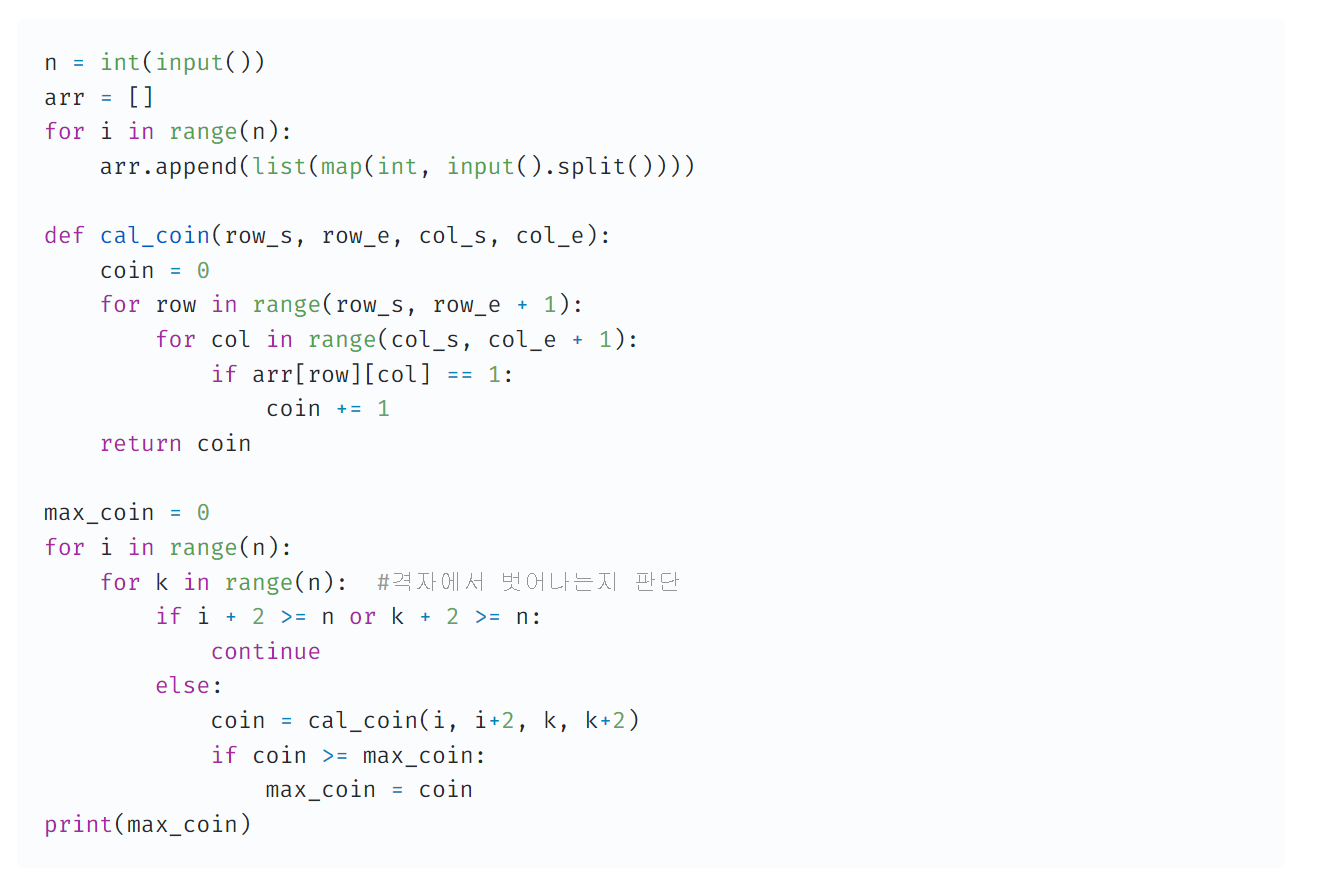
N N 크기의 격자 정보가 주어집니다. 이때 해당 위치에 동전이 있다면 1, 없다면 0이 주어집니다. N N 격자를 벗어나지 않도록 3 * 3 크기의 격자를 적절하게 잘 잡아서 해당 범위 안에 들어있는 동전의 개수를 최대로 하는 프로그램을 작성해보세요.
풀이
n = int(input())
arr = []
for i in range(n):
arr.append(list(map(int, input().split())))
def cal_coin(row_s, row_e, col_s, col_e):
coin = 0
for row in range(row_s, row_e + 1):
for col in range(col_s, col_e + 1):
if arr[row][col] == 1:
coin += 1
return coin
max_coin = 0
for i in range(n):
for k in range(n): #격자에서 벗어나는지 판단
if i + 2 >= n or k + 2 >= n:
continue
else:
coin = cal_coin(i, i+2, k, k+2)
if coin >= max_coin:
max_coin = coin
print(max_coin)- 격자에서는 x, y를 행과 열로 생각하고 왼쪽 모서리에서 부터 커져 간다고 생각하면 편하다
- 3x3 격자에서 벗어나는지 판단하기 위한 if문 사용
- nxn 격자에서 존재할 수 있는 모든 3x3격자를 확인 후 가장 많은 coin을 가지는 경우를 찾는다.
시뮬레이션(Simulation)
시뮬레이션이란 문제에서 주어진 조건대로 특정 작업을 수행하는 걸 의미한다. 앞서 말했듯 문제를 해결하는데 있어 생각이 많이 필요하다기 보다는 머릿속에 떠올린 걸 코드로 옮기는 과정이 어렵다.
1. 격자 안에서 밀고 당기기
밀고 당기는 작업이란 주어진 숫자들을 비트 연산에 shift 와 유사하게 어느 한 쪽 방향으로 한 칸씩 옮겨주는 걸 의미한다. 이를 1차원에 적용하면 좌/우 두 방향, 2차원에 적용하면 상/하/좌/우 네 방향으로 shift 할 수 있다.
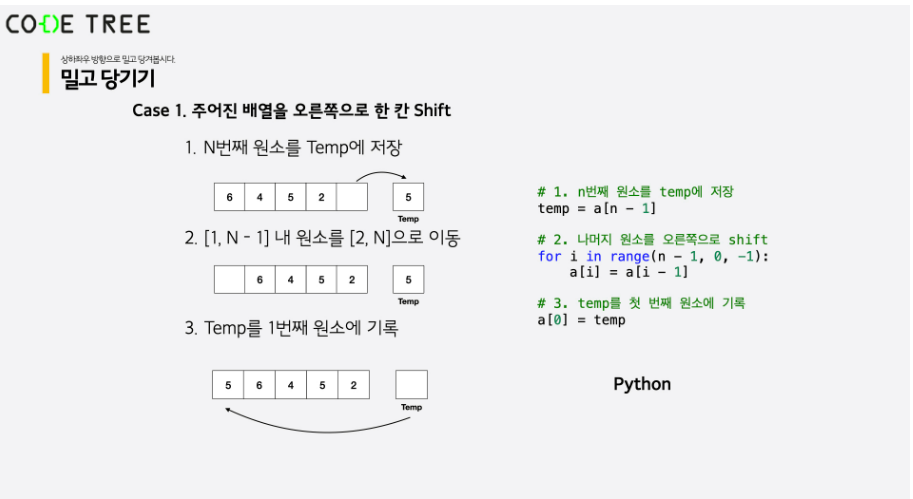
- temp라는 변수에 밀리는 방향에 가장 끝에 있는(ex 오른 쪽으로 민다면 가장 오른쪽에 있는 값) 값을 임시 저장
- 밀리는 방향을 고려하여 한 칸 씩 shift
오른쪽으로 민다면
for i in range(n-1, 0, -1)로 두어야 하는데, 만약for i in range(1, n)으로 둔다면 정보가 유실 되는 현상이 발생하기 때문이다.
- 모든 shift가 끝난 후 temp에 저장되어 있던 값을 첫 번째 칸에 넣어준다.
2. 격자 안에서 터지고 떨어지는 경우
이러한 유형은 폭탄이 터지고 테트리스 처럼 위에 있던 폭탄들이 밑으로 내려오는 문제가 가장 대표적인데 이 문제를 풀 때 한 열에서 폭탄이 터지고 난후의 모습을 구하는데 O(n^2)이 아닌 O(n)만에 구하는 방법을 알아보자.
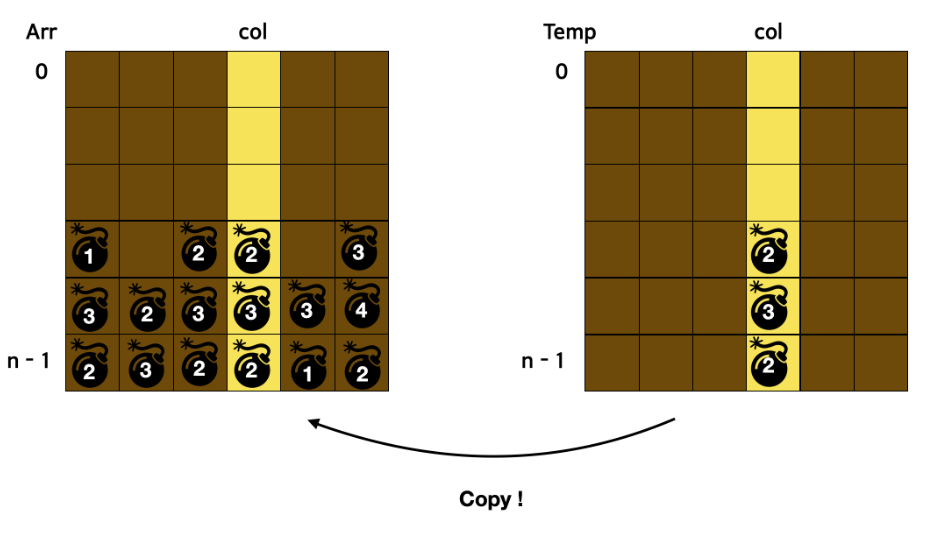
- 폭탄이 동시에 여러 행에서 터져 여러 행에 있는 폭탄이 떨어진다 하더라도 한 열 씩 나눠서 생각
- 격자와 동일한 temp라는 NxN 격자를 생성
- arr의 n-1번 째 행 부터(가장 밑에 있는 행) 위로 올라가면서 폭탄이 있다면 temp 격자의 n-1번째 행부터 시작하여 폭탄을 넣어준다.
- arr을 temp와 일치 시켜준다.
- 이를 모든 열에 반복한다.
이와 같이 풀게 되면 한 열에 폭탄이 터진 모습을 구하는데 O(n)이 걸리므로 격자내 모든 열을 고려하게 된다면 O(n^2)의 수행시간이 걸리게 된다. 이는 격자내 폭탄이 모두 차있다고 할 때 폭탄의 개수가 n^2개 이므로 극악으로 최적화 했을 경우에도 O(n^2)이 걸리게 되는데 이를 lower bound라고 하며 위 방법의 효율이 매우 좋다는 걸 입증한다.
1차원에서 터지고 떨어지는 경우
1차원에서 터지고 떨어지는 경우에는 격자에서 하듯이 위에서 부터 아래로 폭탄이 떨어진다고 생각하지 않고 이를 90도 반시계 방향으로 돌려 기존 리스트 처럼 생각하고 왼 쪽 방향으로 폭탄을 당기는 문제로 변환하여 해결한단. 기존 중력에 의해 밑으로 떨어진다고 생각하는 것과 다르다
1차원 배열은 앞(왼쪽)에서 부터 원소가 채워져 있다고 생각해야 좀 더 직관적이기 때문이다.
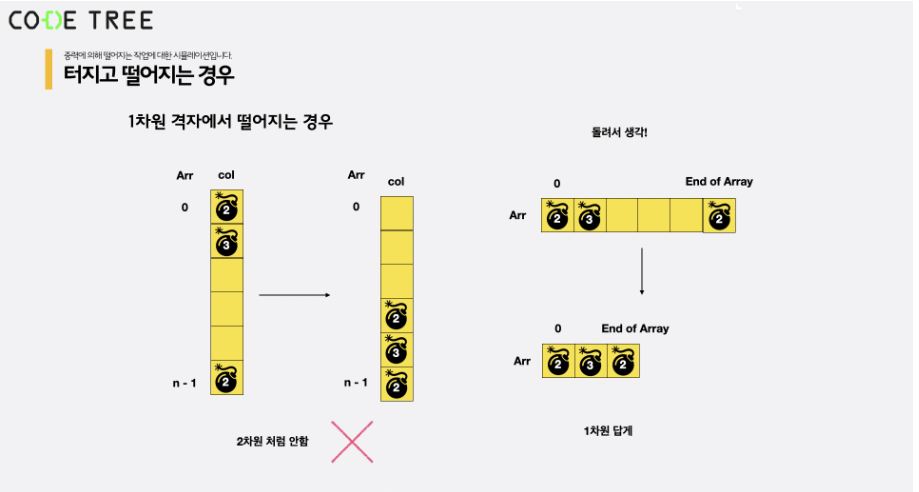
- temp 배열
- arr을 0번 인덱스(왼쪽)에서부터 돌며 폭탄이 있다면 temp 배열에 append()
- arr을 temp와 일치
배열에서 고려해야할 가장 마지막 원소가 있는 index인 end_of_array와 tem 마지막 원소가 들어 있는 index인 end_of_temp를 일치 시켜줘야 한다. 그 이유는 실제로 arr에서 값을 지우는 것이 아닌 0으로만 바꿔주고 왼쪽으로 0이 아닌 값들을 땡겨주는 것이므로 arr의 총 길이인 len(arr)은 변하지 않기 때문이다.
격자 안에서 단일 객체를 이동
격자안에서 dx, dy 테크닉을 사용한 구현 문제를 의미한다.
문제
1이상 100이하의 숫자로 이루어진 n * n 크기의 격자판 정보가 주어집니다. 이때 특정 위치에서 시작하여, 상하좌우로 인접한 곳에 있는 숫자들 중 현재 위치에 있는 숫자보다 더 큰 위치로 끊임없이 이동합니다. 만약 그러한 위치가 여러개 있는 경우, 상하좌우 방향 순서대로 우선순위를 매겨 가능한 곳 중 우선순위가 더 높은 곳으로 이동합니다. 격자를 벗어나서는 안되며, 더 이상 움직일 수 없을 때까지 반복합니다.
풀이
n, x, y = map(int, input().split())
x, y = x-1, y-1
arr = [
list(map(int, input().split()))
for _ in range(n)
]
#상하좌우 순으로 dxs,dys를 구성하여 우선순위를 순서대로 부여
dxs = [-1, 1, 0, 0]
dys = [0, 0, -1, 1]
history = []
history.append(arr[x][y])
def in_range(x, y):
return x >= 0 and x < n and y >= 0 and y < n
flag = 0 #종료 조건을 위한 flag
while flag == 0:
count = 0
for dx, dy in zip(dxs, dys):
count += 1
nx, ny = x + dx, y + dy
if in_range(nx, ny) and arr[nx][ny] > arr[x][y]:
x, y = nx, ny
history.append(arr[nx][ny])
break
if count == 4: #상하좌우 모두 확인 후 x,y가 이동하지 않는 경우(즉, 더 큰 값이 않는 경우)
flag = 1
for h in history:
print(h, end=' ')- 이동시 상하좌우에 우선순위가 부여된다면 dxs, dys를 우선순위가 높은 순서대로 지정하고 비교 시 등호를 ">" 또는 "<"를 사용하면 우선순위가 자동으로 비교 된다.
- in_range()를 통해 격자 범위 내에 위치하는지 판단
- 앞서 dx,dy 편에서도 이야기 했지만 in_range()라는 방어함수를 if문의 첫 번째 조건에 넣어주어야 한다. (이유는dx, dy 테크닉 의 격자 속 dx, dy 참조)
격자 안에서 여러 객체를 이동
격자 안에서 여러 객체가 동시에 이동하는 경우 하나 씩 움직이고 마지막에 전체를 고려한다. 동시에 변화가 일어나는 경우에는 새로운 배열을 만들어 변화모습을 기록하는 게 좋다.
문제
1이상 100이하의 숫자로 이루어진 n * n 크기의 격자판 정보가 주어집니다. 이때 m개 구슬이 서로 다른 위치에서 시작하여 1초에 한 번씩 상하좌우로 인접한 곳에 있는 숫자들 중 가장 큰 값이 적혀있는 숫자가 있는 위치로 동시에 이동합니다. 만약 그러한 위치가 여러개 있는 경우, 상하좌우 방향 순서대로 우선순위를 매겨 가능한 곳 중 우선순위가 더 높은 곳으로 이동합니다. 단, 이때 격자를 벗어나서는 안됩니다.
풀이
n, m, t = map(int, input().split())
arr = [
list(map(int, input().split()))
for _ in range(n)
]
#현재 구슬 위치를 격자에 저장
cur_pos = [
[0 for _ in range(n)]
for _ in range(n)
]
for i in range(m):
x, y = map(int, input().split())
x, y = x - 1, y - 1
cur_pos[x][y] = 1
#상하좌우 순으로 dxs,dys를 구성하여 우선순위를 순서대로 부여
dxs = [-1, 1, 0, 0]
dys = [0, 0, -1, 1]
#격자 내에 있는지 판단
def in_range(x, y):
return x >= 0 and x < n and y >= 0 and y < n
#구슬이 충돌한 경우 처리
def re_dup():
global m
for i in range(n):
for k in range(n):
if next_pos[i][k] > 1:
m -= next_pos[i][k]
next_pos[i][k] = 0
#cur_pos와 next_pos를 일치 시킨다.
def same():
for i in range(n):
for k in range(n):
cur_pos[i][k] = next_pos[i][k]
for i in range(t):
next_pos = [ #구슬의 다음 위치를 저장할 격자
[0 for _ in range(n)]
for _ in range(n)
]
for x in range(n):
for y in range(n):
if cur_pos[x][y] == 1: #구슬이 있는 경우
max_val = 0
for dx, dy in zip(dxs, dys): #상하좌우 모두 확인
nx, ny = x + dx, y + dy
if in_range(nx, ny) and max_val < arr[nx][ny]:
max_val = arr[nx][ny]
tep = (nx, ny)
nx, ny = tep
next_pos[nx][ny] += 1 #구슬의 다음 위치를 next_pos 격자에 저장
re_dup()
same()
print(m)- 구슬의 현재 위치를 저장할 cur_pos, 구슬의 다음 위치를 저장할 next_pos 이차원 배열을 선언한다. 이 때 next_pos는 구슬을 한 번 이동시킨 후 다시 0으로 초기화 되어야 한다.
- cur_pos를 돌며 구슬이 있는 경우 상하좌우 모두 살펴본 후 최대 값이 있는 칸으로 이동하는데 dxs, dys를 상하좌우 순서로 선언했기에 별도의 우선순위를 부여할 필요 없다.
- 구슬 수를 전역변수로 선언하고 함수 안에서 사용시 global 키워드를 붙여준다.