1강 - 벡터
백터가 뭔가요?
벡터는 숫자를 원소로 가지는 리스트 또는 배열이며, 공간에서 한 점을 나타냅니다.
1차원 공간(수직선) - [x]
2차원 공간(좌표평면) - [x, y]
3차원 공간 - [x, y, z]
공간에서 한 점을 나타낸다는 것은, 원점으로부터 상대적 위치를 표현한다고 이해하면 된다.
그러므로 벡터에 숫자를 곱해주면 방향은 그대로, 길이만 변한다.
그리고 벡터끼리 같은 모양을 가지면, 덧셈, 뺄셈을 계산할 수 있다.
벡터의 노름
백터의 노름(norm)은 원점에서부터의 거리를 말한다.
L1-norm: 각 성분의 변화량 절대값을 모두 더한다.
L2-norm: 피타고라스 정리를 이용해 유클리드 거리를 계산한다.
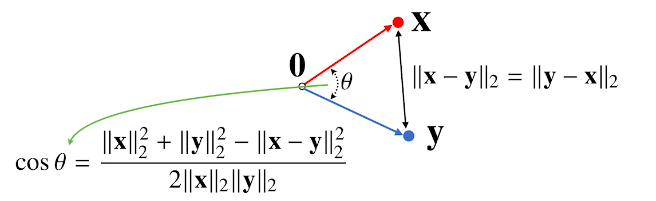
두 벡터 사이의 거리와 각도를 구해보자!
두 벡터 사이의 거리를 계산할 때는 벡터의 뺄셈을 이용한다.
각도는 L2-norm 사이에서만 구할 수 있다.
그리고 제2 코사인 법칙에 의해 두 벡터 사이의 각도를 계산할 수 있고,
쉽게 분자를 계산하는 방법이 내적이다.
2강 - 행렬
행렬은 뭔가요?
행렬(matrix)는 벡터를 원소로 가지는 2차원 배열이다.

행렬은 행(row)과 열(column)이라는 인덱스(index)를 가집니다.
행렬은 특정 행(열)을 고정하면 행(열)벡터라 부릅니다.
전치행렬: 행과 열의 인덱스가 바뀐 행렬을 말한다.
행렬을 이해하는 방법(1)
- 백터가 공간에서의 한 점을 의미한다면 행렬은 여러 점들을 나타낸다고 이해한다.
그렇다면 행렬의 행벡터 xi는 i번째 데이터를, 행렬의 xij는 i번째 데이터의 j번쨰 변수의 값을 의미한다. - 행렬은 벡터를 원소로 가지는 2차원 배열이므로 같은 모양을 가지면 덧셈, 뺄셈 계산할 수 있다.
- 행렬 곱셈은 i번째 행벡터와 j번째 열벡터 사이의 내적을 성분으로 가지는 행렬이 나온다.
numpy 에서는 곱연산을 @ 연산을 사용한다.
(ex)X = np.array([[1,2,3], [4,5,6], [7,8,9]]) Y = np.array([[0,1], [2,0], [1,2]) result = X@Y # result[i][j] = X의 행벡터 xi, Y의 j번쨰 열벡터 곱들의 합 result = array([[7, 7], [16, 16], [25, 25]])
행렬도 내적이 있을까?
numpy의 np.inner 함수는 내적(행렬곱)을 성분으로 가지는 행렬을 계산한다.
```
X = np.array([[1,2,3],
[4,5,6],
[7,8,9]])
Y = np.array([[0,1,2],
[2,0,1],
[1,2,0])
result = np.inner(X, Y)
# result[i][j] = X의 행벡터 xi, Y의 행벡터 yj의 곱들의 합
result = array([[8, 5, 5],
[17, 14, 14],
[26, 23, 23]])
```행렬을 이해하는 방법(2)
행렬은 벡터공간에서 사용되는 연산자로 이해한다. 행렬곱을 통해 벡터를 다른 차원의 공간을 보낼 수 있다.
행렬곱을 통해 패턴을 추출하거나 데이터를 압축할 수 있고, 모든 선형변환은 행렬로 나타낼 수 있다. 기계학습에 많이 쓰인다.
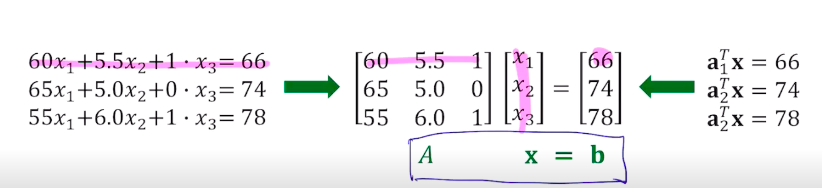
3강 - 선형방정식과 선형 시스템
Identity Matrix (항등행렬) / Inverse Matirx(역행렬)
Identity Matrix: 정사각형의 행렬, (1,1),(2,2),(3,3),, 은 모두 1인 행렬
Inverse Matirx: 정사각의 행렬에 곱해서, 항등행렬을 만들게 해주는 행렬
