트리(Tree)
트리 자료구조는 노드(점)과 그 사이의 간선으로 이루어져있다.
최상단의 노드는 루트 노드, 최하단의 노드는 리프노드, 그 사이 노드는 내부(Internal) 노드
트리의 높이 (Height)
트리의 높이는 최대 level + 1이며, 깊이(depth)라고도 한다.
노드의 차수 (Degree)
노드의 차수란 그 노드의 자식(서브트리)의 수를 말한다.
이진 트리 (binary tree)
이진트리는 재귀적으로 정의할 수 있다.
빈 트리이거나, 루트 노드+왼/오 서브 트리가 이진트리로 되어있는 트리
포화이진트리
모든 레벨에서 노드들이 모두 채워져 있는 이진 트리
높이는 k이고, 노드의 개수가 2의 k승 - 1 개이다.
이진 트리의 연산
- size() - 현재 트리에 포함되어 있는 노드의 수를 구한다.
- depth() - 현재 트리의 깊이 혹은 높이를 구한다.
- 순회(traversal) - 노드를 정해진 순서대로 방문하여 처리한다.
이진 트리의 구현
- 노드 (Node)
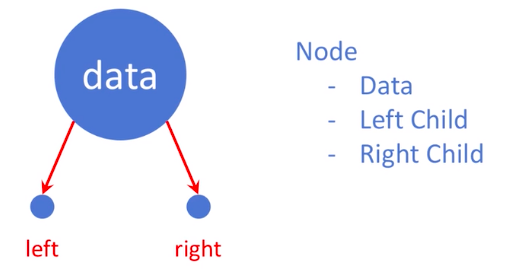
데이터가 담긴 노드와 자식을 가르키는 포인터로 구성된다.
class Node:
def __init__(self, item):
self.data = item
self.left = None
self.right = None- 트리
트리는 루트 노드에 대한 정보만 알면 된다. (노드끼리 연결되어 있기 때문)
class BinaryTree:
def __init__(self, r):
self.root = r- size()
트리의 사이즈(노드 개수)도 재귀적으로 구할 수 있다.
tree.size() = 왼쪽 서브 트리 사이즈 + 오른쪽 서브 트리 사이즈 + 1(자기자신)
class BinaryTree:
def size(self):
if self.root:
return self.root.size()
else:
return 0 - depth()
depth 또한 재귀적으로 구할 수 있다.
전체 이진 트리의 depth() = 왼쪽 서브트리 depth 와 오른쪽 서브트리 depth 중 더 큰 것 + 1
class Node:
def __init__(self, item):
self.data = item
self.left = None
self.right = None
def size(self):
l = self.left.size() if self.left else 0
r = self.right.size() if self.right else 0
return l + r + 1
def depth(self):
l = self.left.depth() if self.left else 0
r = self.right.depth() if self.right else 0
return max(l, r)+1
class BinaryTree:
def __init__(self, r):
self.root = r
def size(self):
if self.root:
return self.root.size()
else:
return 0
def depth(self):
if self.root:
return self.root.depth()
else:
return 0이진 트리의 순회(Traversal)
깊이 우선 순회 (depth first traversal)
- 중위 순회 (in-order traversal)
def inorder(self):
traversal = []
if self.left:
traversal += self.left.inorder()
traversal.append(self.data)
if self.right:
traversal += self.right.inorder()
return traversal- 전위 순회 (pre-order traversal) : 자기 자신부터 순회 -> left subtree -> right subtree
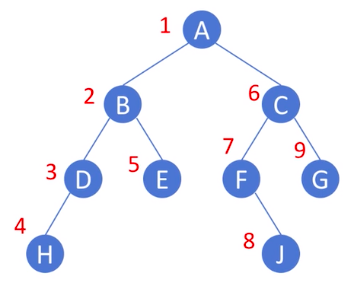
def preorder(self):
traversal = []
traversal.append(self.data)
if self.left:
traversal += self.left.preorder()
if self.right:
traversal += self.right.preorder()
return traversal- 후위 순회 (post-order traversal) : left subtree -> right subtree -> 자기 자신
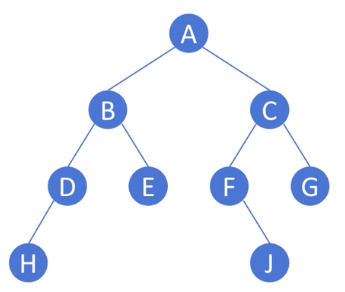
def postorder(self):
traversal = []
if self.left:
traversal += self.left.postorder()
if self.right:
traversal += self.right.postorder()
traversal.append(self.data)
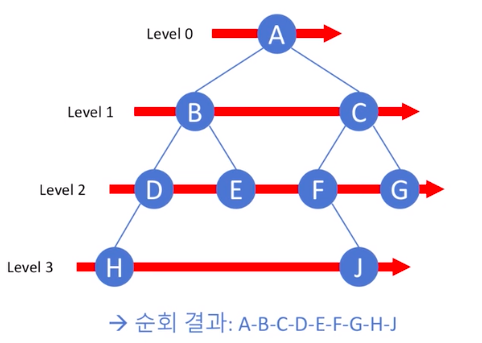
return traversal넓이 우선 순회 (breadth first search)
수준(level)이 낮은 노드를 우선으로 방문,
같은 수준의 노드들 사이에서는 부모 노드의 방문 순서에 따라, 왼쪽부터 오른쪽으로 방문한다.
이 방식은 재귀적 방법으로 구현하지 못한다.
구현할 때 주의할 점
- 한 노드를 방문했을 때, 나중에 방문할 노드들을 순서대로 기억해야 함 -> 큐(queue) 활용
- 먼저 큐를 초기화한다(빈 리스트로) 그 다음, 빈 트리가 아니면 root부터 큐에 삽입한다.
- 큐에서 노드를 하나 꺼내어 방문하는데, 그 노드의 자식 노드를 큐 뒤쪽에 차례대로 삽입한다.
class BinaryTree:
def bft(self):
traversal = []
q = ArrayQueue()
if self.root:
q.enqueue(self.root)
while q.isEmpty() == False:
node = q.dequeue()
traversal.append(node.data)
if node.left:
q.enqueue(node.left)
if node.right:
q.enqueue(node.right)
return traversalPython으로 트리 구현하는 방법 : dictionary(사전) 사용
tree[root] = left, right
tree = {}
tree["A"] = "B", "C"
이렇게 tree의 인덱스는 KEY로, 저장되는 값은 VALUE로 사전에 저장할 수 있다.
{"A" : ("B","C")}
👉 의미 : A가 부모인 노드가 B, C / A의 자식이 B, C
※ A를 key로 가지는 value인 B를 인덱싱하는 방법 : tree["A"][0]
연습 문제 - 이진 트리 높이 구하기 (해커랭크)
def height(root):
tree_h = 0
if root.left and root.right:
tree_lh = 1 + height(root.left)
tree_rh = 1 + height(root.right)
tree_h += max(tree_lh, tree_rh)
elif not root.left and root.right:
tree_rh = 1 + height(root.right)
tree_h += tree_rh
elif root.left and not root.right:
tree_lh = 1 + height(root.left)
tree_h += tree_lh
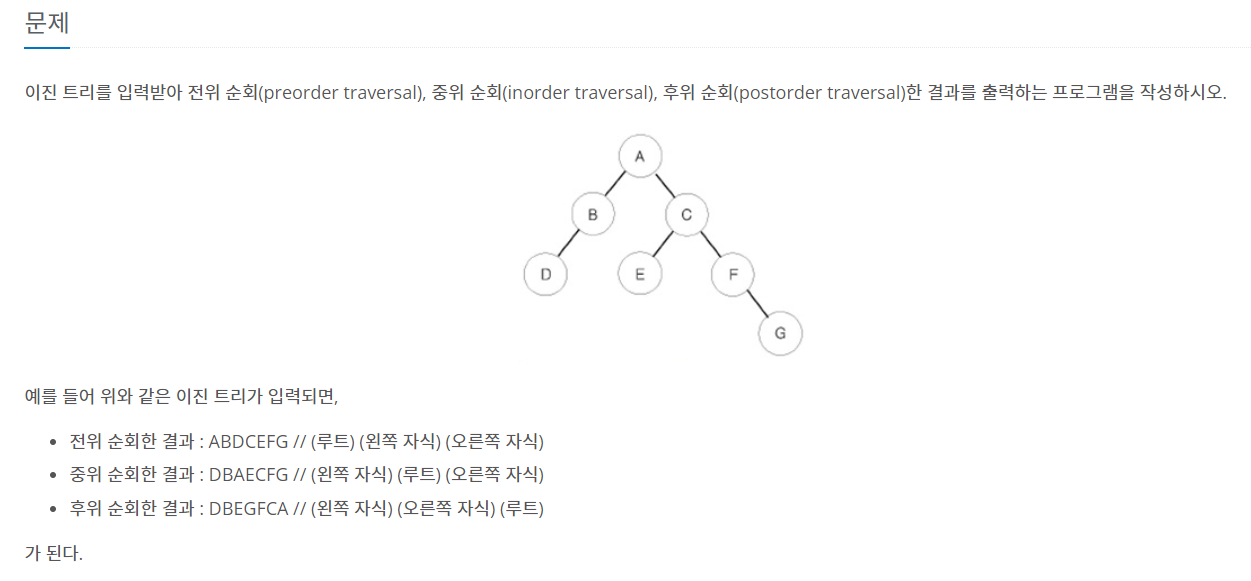
return tree_h연습문제 - 트리 순회 (백준 1991번)
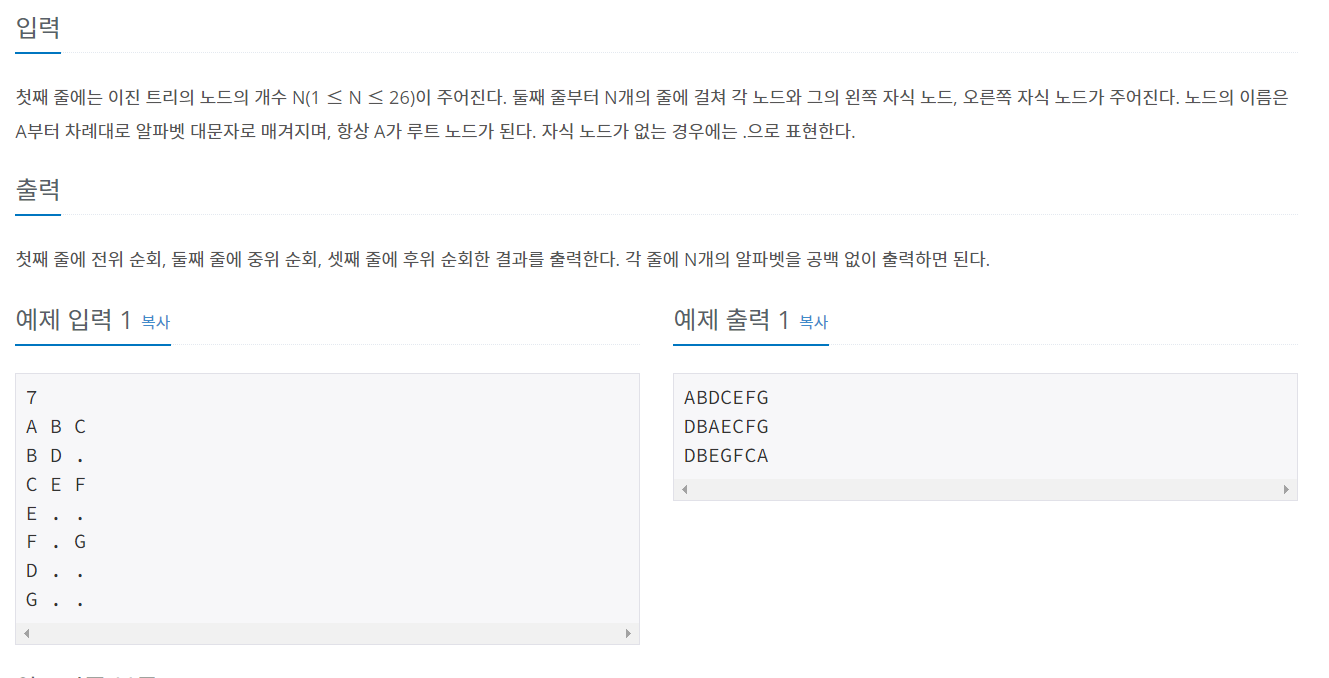
이진 트리의 노드 개수와 노드값들을 입력 받아 각각 전위 순회, 중위 순회, 후위 순회한 결과를 출력하는 문제
import sys
N = int(sys.stdin.readline().strip())
tree = {}
for n in range(N):
root, left, right = sys.stdin.readline().strip().split()
tree[root] = [left, right]
def preorder(root):
if root != '.':
print(root, end='') # root
preorder(tree[root][0]) # left
preorder(tree[root][1]) # right
def inorder(root):
if root != '.':
inorder(tree[root][0]) # left
print(root, end='') # root
inorder(tree[root][1]) # right
def postorder(root):
if root != '.':
postorder(tree[root][0]) # left
postorder(tree[root][1]) # right
print(root, end='') # root
preorder('A')
print()
inorder('A')
print()
postorder('A')연습 문제 - 트리의 부모 찾기 (백준 11725번)

import sys
sys.setrecursionlimit(10**9) # 파이썬 재귀의 깊이 제한: 1000 -> 런타임 에러 발생
def dfs(v):
for i in graph[v]:
if not visited[i]:
visited[i] = v
dfs(i)
n = int(input())
graph = [[] for _ in range(n + 1)]
visited = [0] * (n + 1)
for _ in range(n - 1):
a, b = map(int, sys.stdin.readline().split())
graph[a].append(b)
graph[b].append(a)
dfs(1)
for i in range(2, n + 1):
print(visited[i])