가장 큰 정사각형 찾기
문1) 1와 0로 채워진 표(board)가 있습니다. 표 1칸은 1 x 1 의 정사각형으로 이루어져 있습니다. 표에서 1로 이루어진 가장 큰 정사각형을 찾아 넓이를 return 하는 solution 함수를 완성해 주세요. (단, 정사각형이란 축에 평행한 정사각형을 말합니다.)
예를 들어
| 1 | 2 | 3 | 4 |
|---|---|---|---|
| 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 |
가 있다면 가장 큰 정사각형은
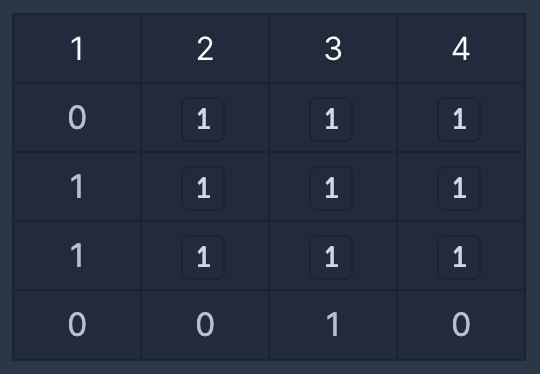
가 되며 넓이는 9가 되므로 9를 반환해 주면 됩니다.
제한사항
- 표(board)는 2차원 배열로 주어집니다.
- 표(board)의 행(row)의 크기 : 1,000 이하의 자연수
- 표(board)의 열(column)의 크기 : 1,000 이하의 자연수
- 표(board)의 값은 1또는 0으로만 이루어져 있습니다.
입출력 예
| board | answer |
|---|---|
[[0,1,1,1],[1,1,1,1],[1,1,1,1],[0,0,1,0]] | 9 |
[[0,0,1,1],[1,1,1,1]] | 4 |
입출력 예 설명
입출력 예 #2
| 0 | 0 | 1 | 1 |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
로 가장 큰 정사각형의 넓이는 4가 되므로 4를 return합니다.
나의 풀이
package programmers;
public class FindTheLargestSquare {
public static int solution(int [][]board) {
int answer = 0;
int row = board.length;
int col = board[0].length;
if(row < 2 || col < 2) {
for(int i = 0; i < row; i++) {
for(int j = 0; j < col; j++) {
if(board[i][j] == 1) {
return 1;
}
}
}
return 0;
}
for(int i = 1; i < row; i++) {
for(int j = 1; j < col; j++) {
if(board[i][j] == 1) {
board[i][j] = Math.min(board[i-1][j-1], Math.min(board[i-1][j], board[i][j-1])) + 1;
answer = Math.max(answer, board[i][j]);
}
}
}
return answer * answer;
}
public static void main(String[] args) {
int[][] board = {{0,1,1,1},{1,1,1,1},{1,1,1,1},{0,0,1,0}};
solution(board);
}
}
줄 서는 방법
문2) n명의 사람이 일렬로 줄을 서고 있습니다. n명의 사람들에게는 각각 1번부터 n번까지 번호가 매겨져 있습니다. n명이 사람을 줄을 서는 방법은 여러가지 방법이 있습니다. 예를 들어서 3명의 사람이 있다면 다음과 같이 6개의 방법이 있습니다.
- [1, 2, 3]
- [1, 3, 2]
- [2, 1, 3]
- [2, 3, 1]
- [3, 1, 2]
- [3, 2, 1]
사람의 수 n과, 자연수 k가 주어질 때, 사람을 나열 하는 방법을 사전 순으로 나열 했을 때, k번째 방법을 return하는 solution 함수를 완성해주세요.
제한사항
- n은 20이하의 자연수 입니다.
- k는 n! 이하의 자연수 입니다.
입출력 예
| n | k | result |
|---|---|---|
| 3 | 5 | [3,1,2] |
나의 풀이
메모리 초과 및 효율성 실패 로직
package programmers;
import java.util.ArrayList;
public class HowToStandInLine {
static ArrayList<int[]> list = new ArrayList<>();
public static void generateCombinations(int[] combination, int n, int idx) {
if(idx == n) {
list.add(combination.clone());
return;
}
for(int i = 1; i <= n; i++) {
if(contains(combination, idx, i)) continue;
combination[idx] = i;
generateCombinations(combination, n, idx + 1);
}
}
public static boolean contains(int[] arr, int untilIdx, int val) {
for(int i = 0; i < untilIdx; i++) {
if(arr[i] == val) {
return true;
}
}
return false;
}
public static int[] solution(int n, long k) {
int[] answer = new int[n];
int[] combination = new int[n];
generateCombinations(combination, n, 0);
for(int i = 0; i < answer.length; i++) {
answer[i] = list.get((int)(k-1))[i];
}
return answer;
}
public static void main(String[] args) {
solution(3, 5);
}
}
1. 전체 개요
- n까지의 정수로 만들 수 있는 모든 순열을 생성하고, k 번째 순열을 반환하는 문제이다.
예를들어, n = 3이고 k = 5라면, 가능한 순열을 [1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1] 이며, 5번째 순열인 [3,1,2]를 반환한다.
2. 메서드 설명
a. generateCombinations
- 주어진 n 값에 대해 가능한 모든 순열을 재귀적으로 생성
- combination : 현재까지 생성된 부분 순열을 저장하는 배열
- idx : 현재 순열에서 채워야 할 위치
- n : 순열의 최대 크기
- idx가 n과 같아지면, 완전한 순열이 생성된 것이므로 list에 추가. 그렇지 않다면, 가능한
모든 숫자 i에 대해 combination[idx]에 i를 할당하고 재귀적으로 다음 위치 idx + 1로 넘어감
b. contains
- 배열 arr에 값 val이 이미 포함되어 있는지 여부를 확인하는 로직. untilIdx는 확인해야 할 배열의 최대 인덱스를 나타냄. 즉, 이 메서드는 배열의 0부터 untilIdx - 1 까지의 요소 중에서 val이 있는지 검사
c. solution
- 순열을 저장할 answer 배열과 순열을 생성하기 위한 작업 배열 combination을 초기화함
- generateCombinations 메서드를 호출하여 가능한 모든 순열을 list에 저장
- 마지막으로, list에서 k-1 번째 순열을 answer 배열에 복사하여 반환
개선된 로직
package programmers;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class HowToStandInLine {
public static long factorial(int n) {
long result = 1;
for (int i = 1; i <= n; i++) {
result *= i;
}
return result;
}
public static int[] solution(int n, long k) {
List<Integer> numbers = new ArrayList<>();
for(int i = 1; i <= n; i++) {
numbers.add(i);
}
int[] answer = new int[n];
k--;
for(int i = 0; i < n; i++) {
long fact = factorial(n - i - 1);
int index = (int) (k / fact);
answer[i] = numbers.remove(index);
k %= fact;
}
return answer;
}
public static void main(String[] args) {
solution(3, 5);
}
}
나의 생각
k번째 순열을 효율적으로 찾는 방법
이 문제의 핵심은 factorial이다. 따라서, 매개변수로 주어진 n에 대해 가능한 모든 순열이 factorial에 기반하여 어떻게 분배되는지를 파악하는 것이다.
예를들어, n = 3일 때, 숫자들 1,2,3으로 만들 수 있는 순열은 총 6개 (3!)이다.
- 1로 시작하는 순열 :
1,2,3,1,3,2(총 2개 = 2!) - 2로 시작하는 순열 :
2,1,3,2,3,1(총 2개 = 2!) - 3으로 시작하는 순열 :
3,1,2,3,2,1(총 2개 = 2!)
k = 5일 때 k--를 하는데, 그 이유는 k는 1-based로 표시되어 있기때문에 k번째 순열을 착기 위해 indexing을 조정해야한다.
k = 5라면, 5번째 순열인 3,1,2를 찾아야하는데, 0-based 인덱싱을 사용할 때, 5번째 순열은 실제로 index 4에 위치하게된다.
따라서 시작할 때 k = 4 , numbers = {1,2,3}
1. 첫 번째 숫자 찾기
n - 1인 2의 팩토리얼 값은 2! = 2
k = 4를 2!로 나눈 값(몫)은 2이며, 나머지는 0, 이는 numbers[2]를 의미함
따라서 answer[0] = numbers[2] = 3이 들어감
사용된 숫자 3은 numbers 리스트에서 제거
numbers = {1,2}
2. 두 번째 숫자 찾기
n - 2인 1의 팩토리얼 값은 1! = 1
현재의 k 값은 이전 계산의 나머지 0
k = 0을 1!로 나눈 값(몫)은 0이며, 나머지는 0, 이는 numbers[0]을 의미함
따라서 answer[1] = numbers[0] = 1이 들어감
사용된 숫자 1은 numbers 리스트에서 제거
numbers = {2}
3. 세 번째 숫자 찾기
이제 numbers 리스트에는 오직 하나의 숫자만 남음
따라서 answer[2]에는 numbers 리스트의 마지막 숫자인 2가 들어감
결과적으로 answer 배열은 [3,1,2]가 됨
점 찍기
문3) 좌표평면을 좋아하는 진수는 x축과 y축이 직교하는 2차원 좌표평면에 점을 찍으면서 놀고 있습니다. 진수는 두 양의 정수 k, d가 주어질 때 다음과 같이 점을 찍으려 합니다.
- 원점(0, 0)으로부터 x축 방향으로 ak(a = 0, 1, 2, 3 ...), y축 방향으로 bk(b = 0, 1, 2, 3 ...)만큼 떨어진 위치에 점을 찍습니다.
- 원점과 거리가 d를 넘는 위치에는 점을 찍지 않습니다.
예를 들어, k가 2, d가 4인 경우에는 (0, 0), (0, 2), (0, 4), (2, 0), (2, 2), (4, 0) 위치에 점을 찍어 총 6개의 점을 찍습니다.
정수 k와 원점과의 거리를 나타내는 정수 d가 주어졌을 때, 점이 총 몇 개 찍히는지 return 하는 solution 함수를 완성하세요.
제한사항
- 1 ≤ k ≤ 1,000,000
- 1 ≤ d ≤ 1,000,000
입출력 예
| k | d | result |
|---|---|---|
| 2 | 4 | 6 |
| 1 | 5 | 26 |
입출력 예 설명 #2
- (0, 0), (0, 1), (0, 2), (0, 3), (0, 4), (0, 5), (1, 0), (1, 1), (1, 2), (1, 3), (1, 4), (2, 0), (2, 1), (2, 2), (2, 3), (2, 4), (3, 0), (3, 1), (3, 2), (3, 3), (3, 4), (4, 0), (4, 1), (4, 2), (4, 3), (5, 0) 위치에 점을 찍을 수 있으며, 총 26개 입니다.
나의 풀이
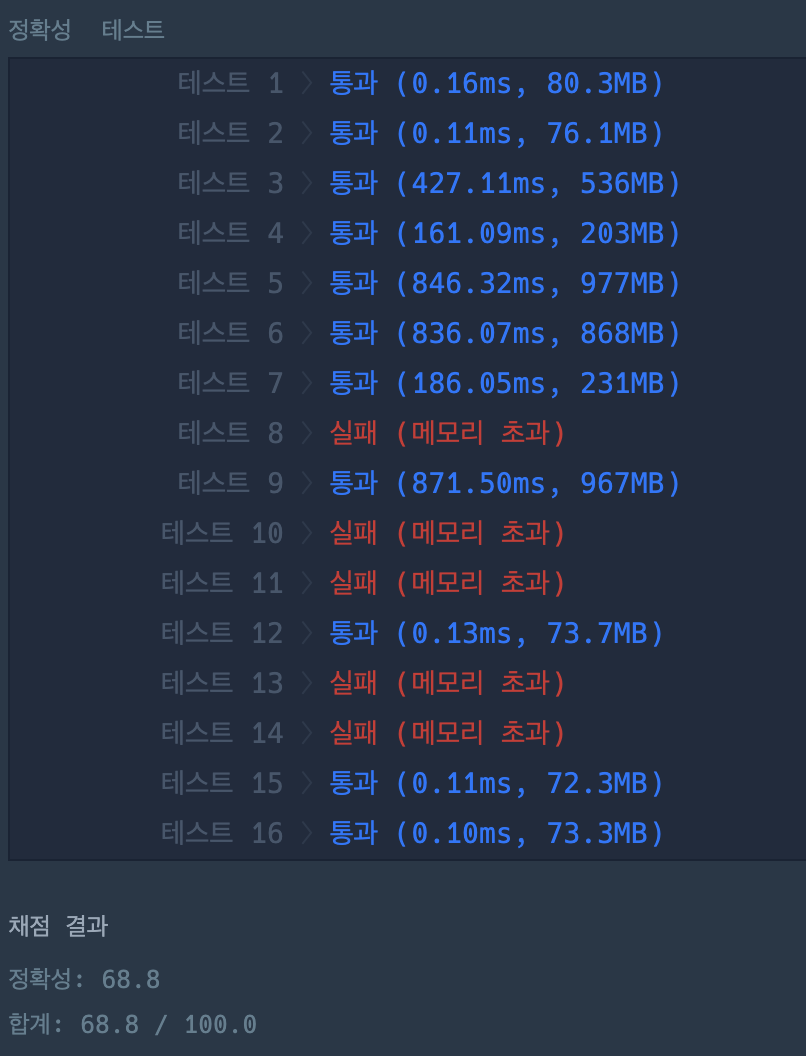
메모리 초과 (실패) 로직
- 알고리즘
Lv2문제를 풀면서, 점점 시간 복잡도와, 메모리를 신경써야 할 때가 온 것 같다.
이번 문제 역시, 의식의 흐름대로 문제를 접근하니 메모리 초과(실패) 해버렸다..
package programmers;
import java.util.ArrayList;
import java.util.List;
public class DrawADot {
public static long solution(int k, int d) {
List<Long> list = new ArrayList<>();
ArrayList<long[]> dotList = new ArrayList<>();
long dot = 0;
int i = -1;
while(true) {
i++;
if(i * k > d) break;
dot = i * k;
list.add(dot);
}
for(int m = 0; m < list.size(); m++) {
for(int n = 0 ; n < list.size(); n++) {
long[] coor = new long[2];
long x = list.get(m);
long y = list.get(n);
double distance = Math.sqrt((Math.pow(x, 2) + Math.pow(y, 2)));
if(distance <= (double)d) {
coor[0] = x;
coor[1] = y;
dotList.add(coor.clone());
}
}
}
return dotList.size();
}
public static void main(String[] args) {
solution(1, 5);
}
}
메모리 초과 문제를 해결한 로직
package programmers;
public class DrawADot {
public static long solution(int k, int d) {
long total = 0;
for(int x = 0; x <= d; x += k) {
long dSquare = (long) d * d;
long xSquare = (long) x * x;
int maxY = (int) Math.sqrt(dSquare - xSquare);
total += (maxY / k) + 1;
}
return total;
}
public static void main(String[] args) {
solution(2, 4);
}
}
나의 생각
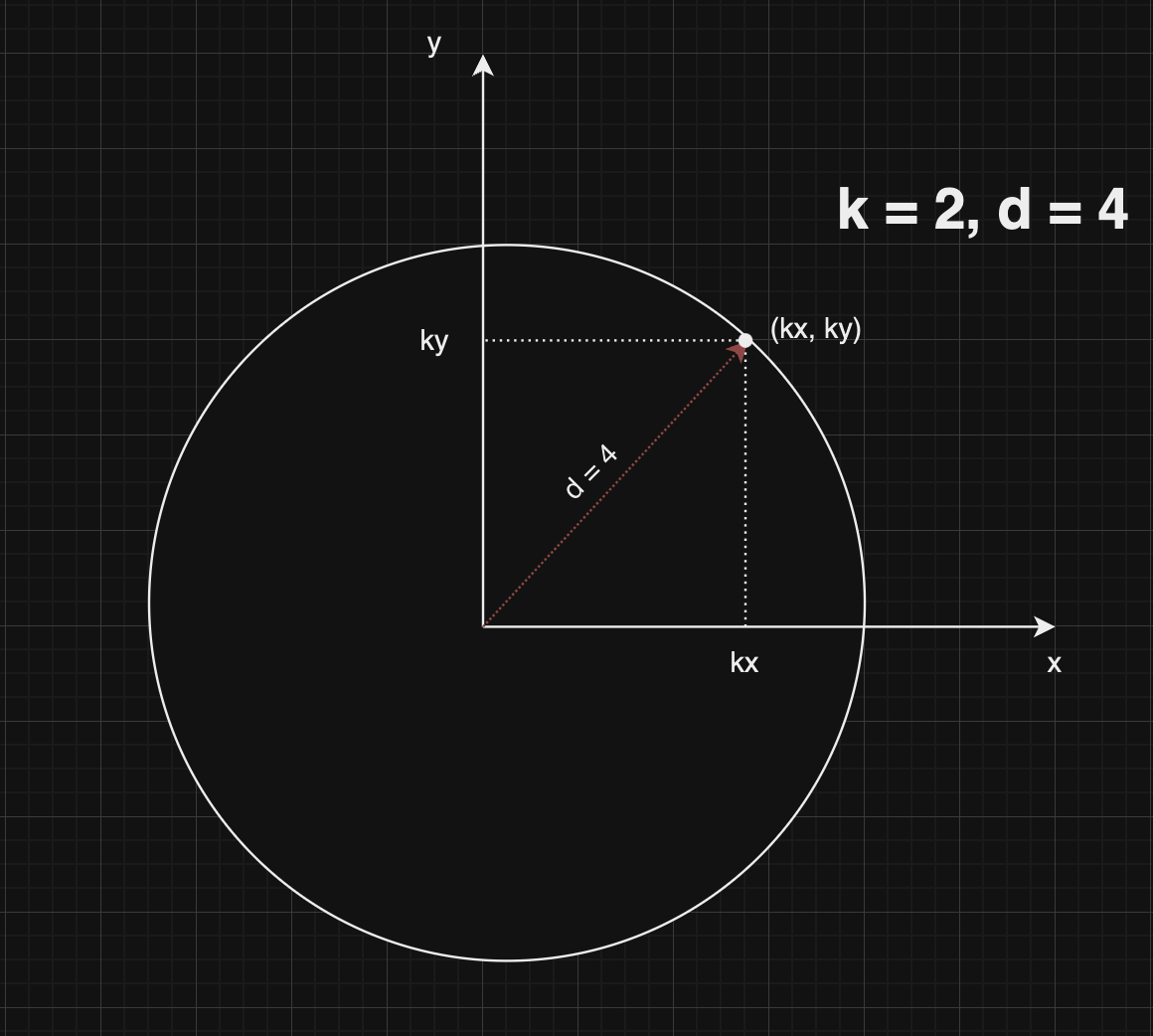
먼저, 문제를 정리해보면, 거리가 d 이하인 x,y 좌표 정수의 개수를 구하는 문제이다.
그림을 그려보면 익숙한 그림이 나오는데, 원점에서의 거리가 d인 점을 포함하는 원을 생각하면,
방정식이 도출된다. 문제에서 원점으로부터 거리가 d를 초과하는 점은 제외한다고 했으므로, 원 위나 원 안에 있는 점만을 고려하면 된다.
원 위의 임의의 점(x,y)에 대해, 원점과 해당 점을 직선으로 연결하면 그 길이는 원의 반지름인 d가 된다. 이때, 원점에서 x만큼 수평으로 이동한 위치와 y만큼 수직으로 이동한 위치 사이의 거리 또한 d이다. 이를 직각삼각형의 형태로 생각하면 x와 y는 직각변이 되고, 원점에서(x,y)까지의 선분이 빗변이 된다. 이때, 피타고라스의 정리에 따라 x^2 + y^2 = d^2을 만족하고, y에 대해서 정리하면 다음과 같다.
문제의 핵심은 일반적으로 이중 for문으로 문제를 해결할 수 있지만, 이렇게되면 최악의 경우
x와 y 각각에 대해 최대 d/k번의 반복을 의미한다.
따라서, k = 1, d = 1,000,000 경우 O(1,000,000,000,000) 1조번의 연산이 필요하다... 그렇기 때문에, 위에서 언급한
위 식을 적용하면, for문을 한번 순회 하는 것으로 y값을 도출 할 수 있다.
핵심 로직은 다음과 같다.
for(int x = 0; x <= d; x += k) {
long dSquare = (long) d * d;
long xSquare = (long) x * x;
int maxY = (int) Math.sqrt(dSquare - xSquare);
total += (maxY / k) + 1 ;
}x = 0일 때,
maxY = 4
가능한 y의 값은 0,2,4
x = 2일 때,
maxY = 3
가능한 y의 값은 0,2
x = 4일 때,
maxY = 0
가능한 y의 값은 0
따라서, 점의 총 갯수는 6개 (0,0),(0,2),(0,4),(2,0),(2,2),(4,0)
미로 탈출
문4) x 1 크기의 칸들로 이루어진 직사각형 격자 형태의 미로에서 탈출하려고 합니다. 각 칸은 통로 또는 벽으로 구성되어 있으며, 벽으로 된 칸은 지나갈 수 없고 통로로 된 칸으로만 이동할 수 있습니다. 통로들 중 한 칸에는 미로를 빠져나가는 문이 있는데, 이 문은 레버를 당겨서만 열 수 있습니다. 레버 또한 통로들 중 한 칸에 있습니다. 따라서, 출발 지점에서 먼저 레버가 있는 칸으로 이동하여 레버를 당긴 후 미로를 빠져나가는 문이 있는 칸으로 이동하면 됩니다. 이때 아직 레버를 당기지 않았더라도 출구가 있는 칸을 지나갈 수 있습니다. 미로에서 한 칸을 이동하는데 1초가 걸린다고 할 때, 최대한 빠르게 미로를 빠져나가는데 걸리는 시간을 구하려 합니다.
미로를 나타낸 문자열 배열 maps가 매개변수로 주어질 때, 미로를 탈출하는데 필요한 최소 시간을 return 하는 solution 함수를 완성해주세요. 만약, 탈출할 수 없다면 -1을 return 해주세요.
제한사항
- 5 ≤ maps의 길이 ≤ 100
- 5 ≤ maps[i]의 길이 ≤ 100
- maps[i]는 다음 5개의 문자들로만 이루어져 있습니다.
- S : 시작 지점
- E : 출구
- L : 레버
- O : 통로
- X : 벽
- 시작 지점과 출구, 레버는 항상 다른 곳에 존재하며 한 개씩만 존재합니다.
- 출구는 레버가 당겨지지 않아도 지나갈 수 있으며, 모든 통로, 출구, 레버, 시작점은 여러 번 지나갈 수 있습니다.
입출력 예
| maps | result |
|---|---|
| ["SOOOL","XXXXO","OOOOO","OXXXX","OOOOE"] | 16 |
| ["LOOXS","OOOOX","OOOOO","OOOOO","EOOOO"] | -1 |
입출력 예 설명
입출력 예 #1
주어진 문자열은 다음과 같은 미로이며
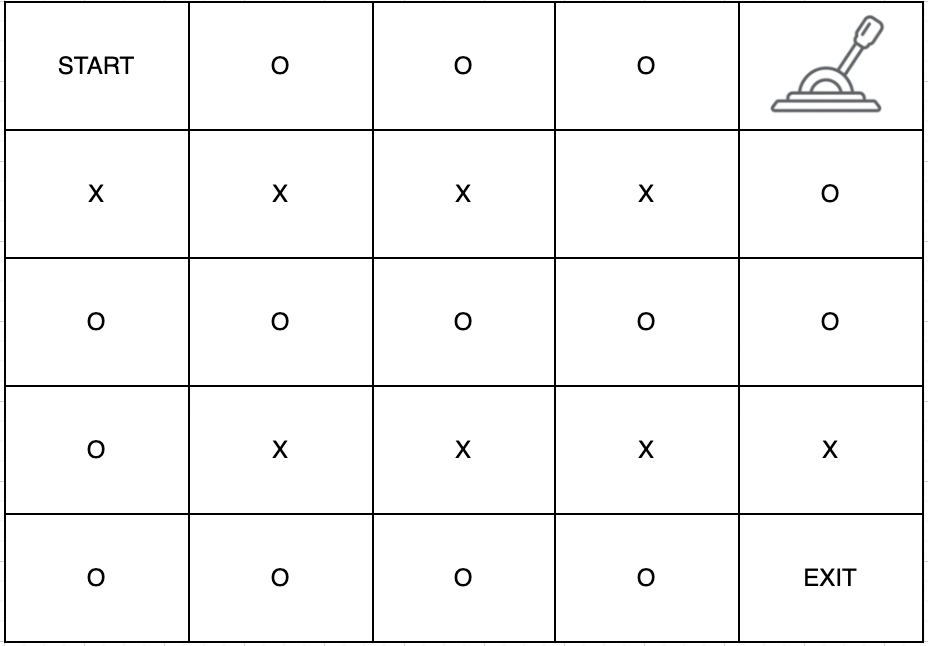
다음과 같이 이동하면 가장 빠른 시간에 탈출할 수 있습니다.

4번 이동하여 레버를 당기고 출구까지 이동하면 총 16초의 시간이 걸립니다. 따라서 16을 반환합니다.
입출력 예 #2
주어진 문자열은 다음과 같은 미로입니다.
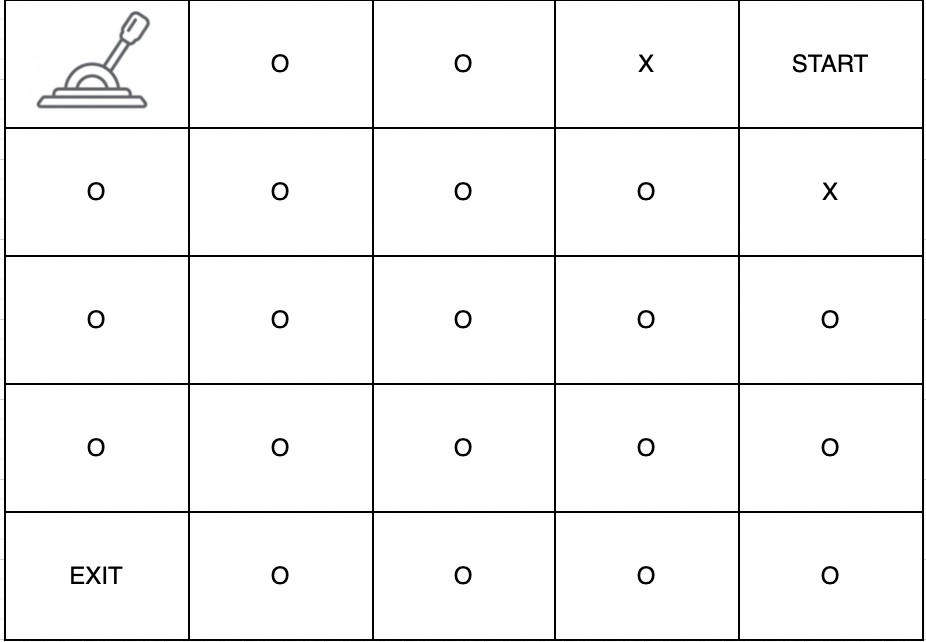
시작 지점에서 이동할 수 있는 공간이 없어서 탈출할 수 없습니다. 따라서 -1을 반환합니다.
나의 풀이
package programmers;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
public class MazeEscape {
static int[][] DIRS = {{-1,0},{1,0},{0,-1},{0,1}}; //상하좌우;
public static int[] bfs(char[][] maze, int startX, int startY, char target ) {
System.out.printf("startX: %d, startY: %d, tartget: %c\n",startX,startY, target);
int n = maze.length;
int m = maze[0].length;
boolean[][]visited = new boolean[n][m];
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[] {startX, startY, 0});
for(int[] a : queue) {
System.out.println(Arrays.toString(a));
}
while(!queue.isEmpty()) {
int[] current = queue.poll();
int x = current[0];
int y = current[1];
int distance = current[2];
System.out.printf("x: %d, y: %d, dis: %d\n",x,y,distance);
if(maze[x][y] == target) return new int[] {x,y,distance};
for(int i = 0; i < 4; i++) {
int nx = x + DIRS[i][0];
int ny = y + DIRS[i][1];
if(nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
if(maze[nx][ny] == 'X' || visited[nx][ny]) continue;
visited[nx][ny] = true;
queue.add(new int[] {nx, ny, distance + 1});
}
}
return new int[] {-1, -1, -1};
}
public static int solution(String[] maps) {
int n = maps.length;
int m = maps[0].length();
char[][] maze = new char[n][m];
int startX = 0, startY = 0;
for(int i = 0; i < n; i++) {
for(int j = 0; j < m; j++) {
maze[i][j] = maps[i].charAt(j);
if(maze[i][j] == 'S') {
startX = i;
startY = j;
}
}
}
int[] leverPosition = bfs(maze, startX, startY, 'L');
if(leverPosition[2] == -1) return -1;
int fromLeverToEnd = bfs(maze, leverPosition[0], leverPosition[1], 'E')[2];
if(fromLeverToEnd == -1) return -1;
System.out.println(leverPosition[2] + fromLeverToEnd);
return leverPosition[2] + fromLeverToEnd;
}
public static void main(String[] args) {
String[] maps = {"SOOOL","XXXXO","OOOOO","OXXXX","OOOOE"};
solution(maps);
}
}
