실력진단

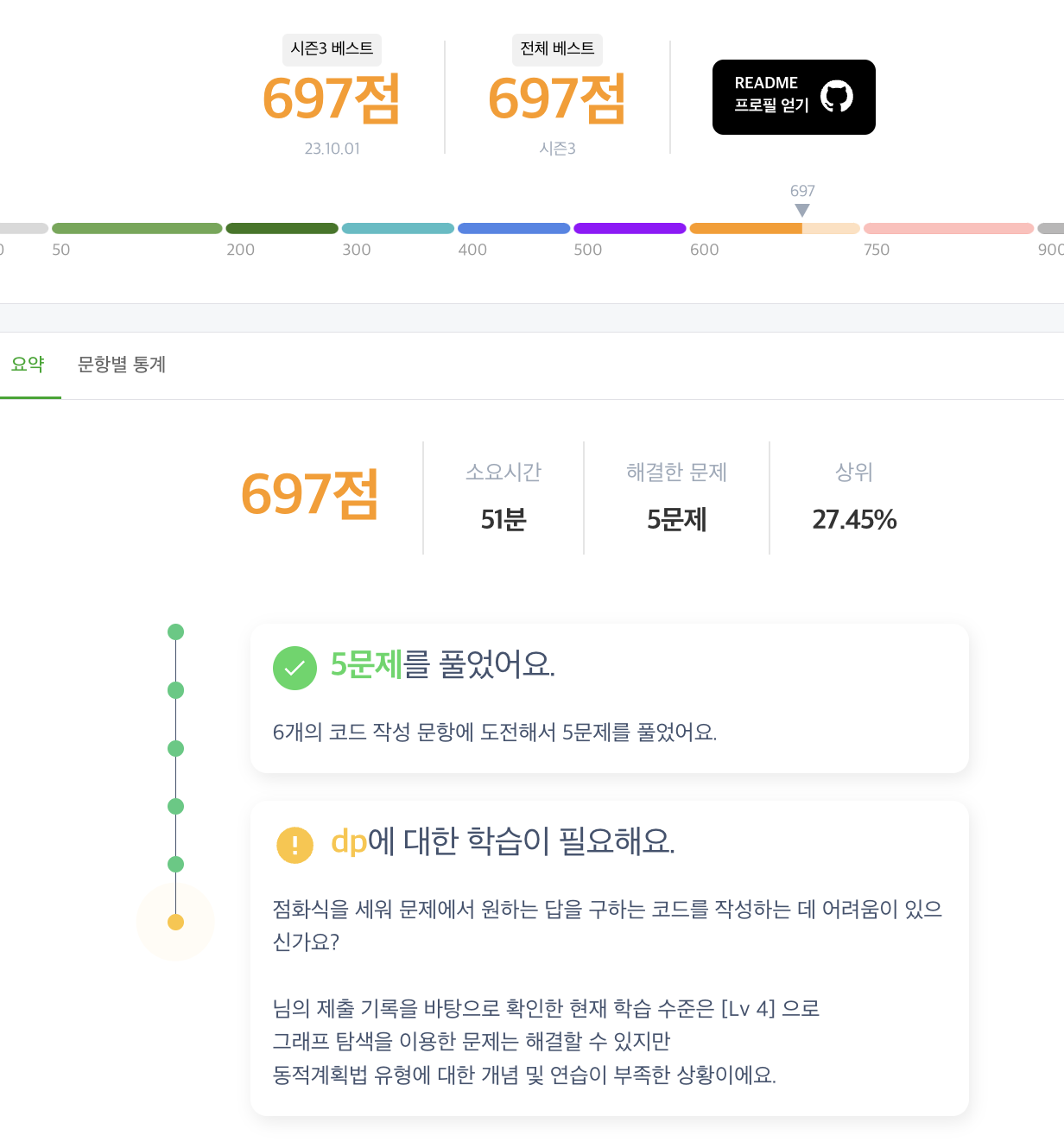
매 시험마다 한문제씩 더 클리어 하는 중 🤣
DP 는 예전부터 어려워했던 유형인데, 이번에 잘 못풀어서 다시 공부를 했다.

DP 는 2가지 방식으로 풀 수 있는데 Memoization 과 Tabulation.

Memoization 은 탑다운 방식이고 Tabulation 바텀업 방식으로 위와 아래 중 어디부터 데이터를 저장하느냐의 차이다.

둘의 시간복잡도는 이론상 동일하지만, 재귀이기에 추가되는 함수 처리 시간이 더 붙기 때문에, 바텀업 방식이 더 빠르다.

연습문제

그래서 이번 문제에 대한 보완 문제로는 이 문제가 추천으로 나왔다.

문제 : https://www.codetree.ai/missions/2/problems/maximum-sum-path-in-square/description

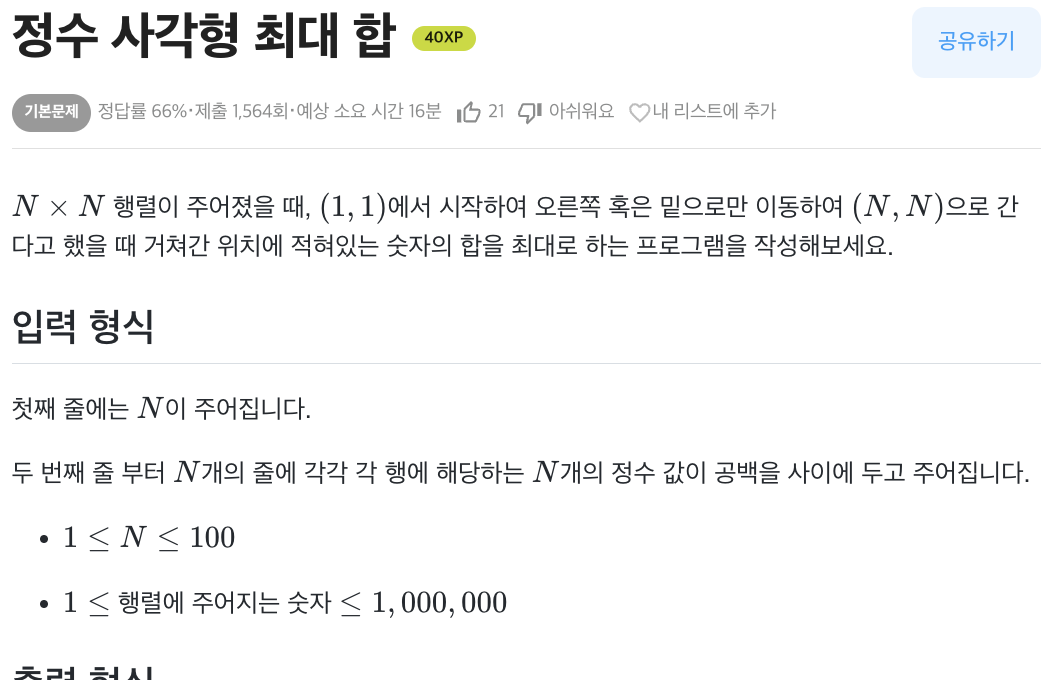
나는 바텀업 방식으로 접근했고, 먼저 맨 왼쪽과 맨 위쪽 행렬의 합을 구해준 후 나머지를 채우는 방식으로 접근했다.

n = int(input())

grid = []
dp = [[0] * n for _ in range(n)]
for i in range(n):
    arr = list(map(int, input().split()))
    grid.append(arr)


dp[0][0] = grid[0][0]

for i in range(1, n):
    dp[i][0] = dp[i-1][0] + grid[i][0]

for j in range(1, n):
    dp[0][j] = dp[0][j-1] + grid[0][j]


for i in range(1, n):
    for j in range(1, n):
        dp[i][j] = max(dp[i-1][j] + grid[i][j], dp[i][j-1] + grid[i][j]) 


print(dp[n-1][n-1])

왜냐하면 냅다

dp[i][j] = max(dp[i-1][j] + grid[i][j], dp[i][j-1] + grid[i][j]) 

이것부터 작성한다면, 맨왼쪽과 맨 위쪽 행열은 오류가 나기 때문이다. (각 행 또는 열에서 -1 한 행렬값을 가져오므로)

후기

dp 쪽은 어려워서 몇 문제 못풀어봤는데, 이번주에는 dp 를 열심히 공부해봐야겠다!