백준15829번:Hashing

인트로:

이번 백준 문제는 15829번 Hashing이다.

문제:

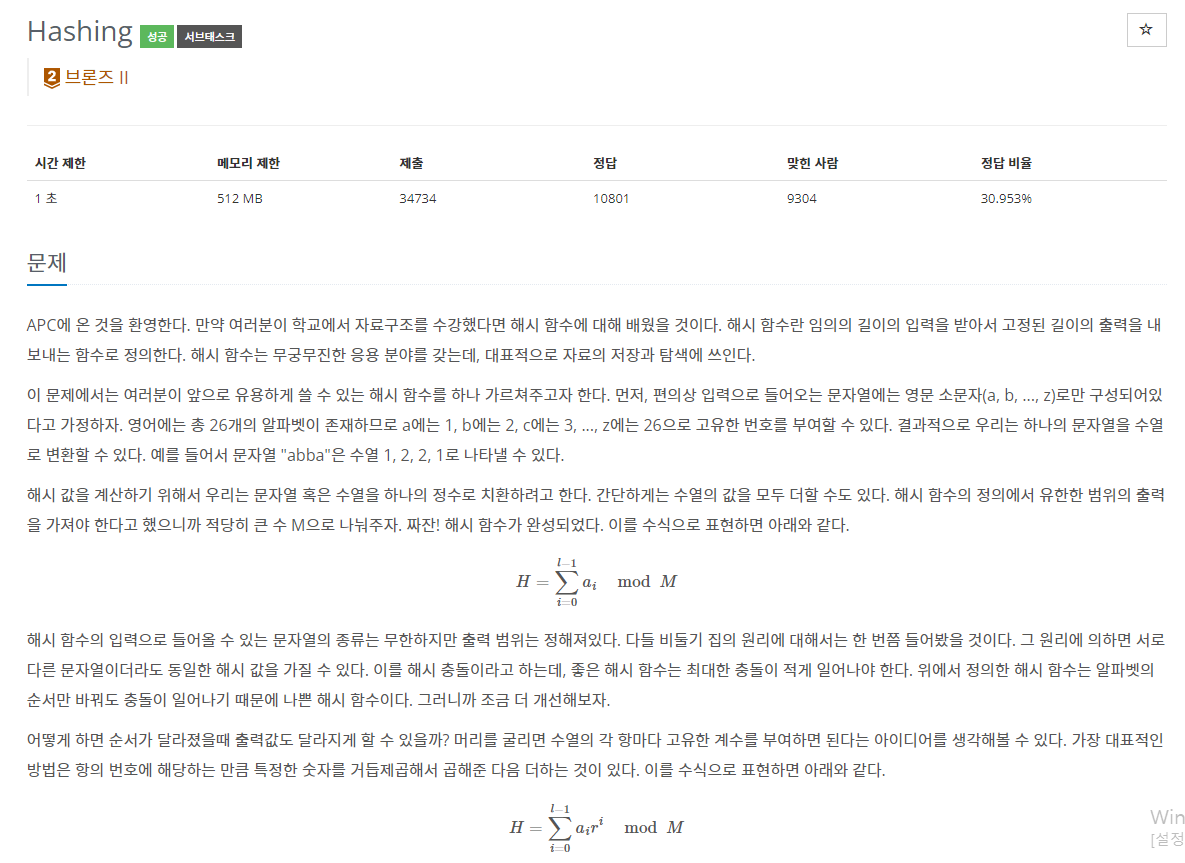
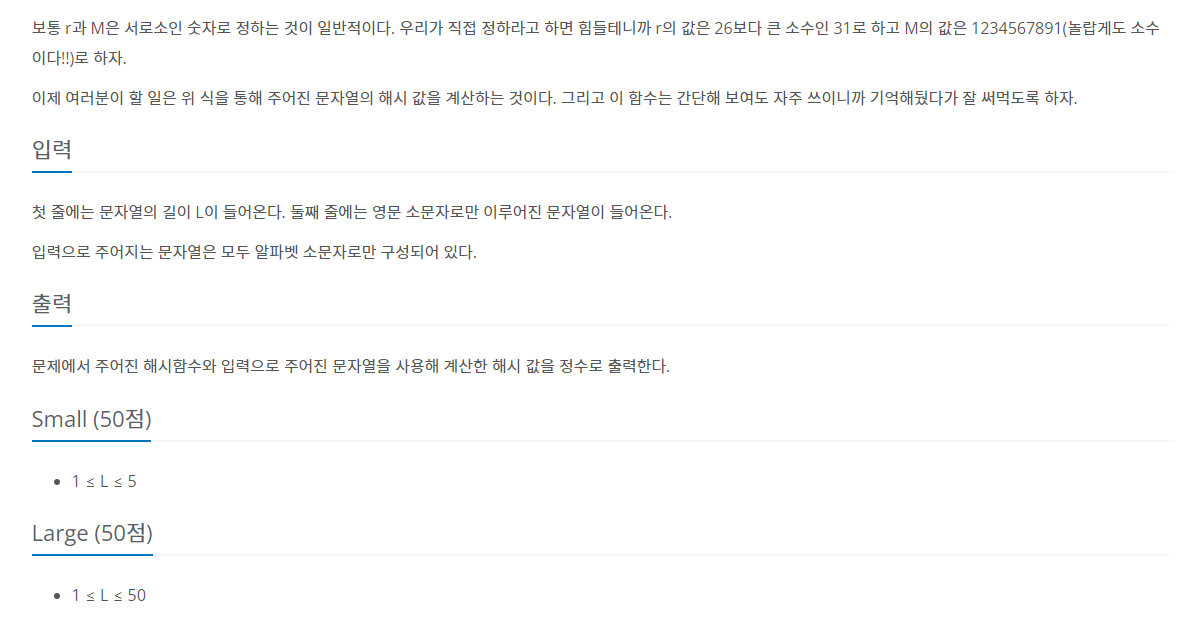
문제해석:

문제에서 r의 값은 31, M의 값은 123456789로 정했다.
이 문제에서는 해쉬 알고리즘 연산에 대한 지식을 요하는 문제여서 바로 찾아봤다.

아래에 식을 통해서 모듈러 연산이 사용된다는것을 알아낼 수 있었다.

모듈로 연산(Modulo Arithmetic)

모듈로 n 연산이란 (n은 양의 정수)
정수 a와 양의 정수 n //a 와 n 은 서로소의 관계를 가지고 있다.
a mod n = r
r은 a를 n으로 나눈 나머지다.
문제에서는 r 값을 31로 정하고 모듈갑을 1234567891로 정했다.

분배 법칙(distribution rule)

암호연산에서 가장 많이 사용되는 법칙으로 세가지가 있다.

• 덧셈의 분배법칙:(a+b)mod n=[a(a mod n) + (b mod n)]mod n
• 뺄셈의 분배법칙:(a-b)mod n=[a(a mod n) - (b mod n)]mod n
• 곱셈의 분배법칙:(axb)mod n=[a(a mod n) x (b mod n)]mod n

코드:

느낀점:

백준2609번 최대,최소 공약수에서 유클리드 호제법을 사용했다면, 이번문제에서 모듈러 연산을 사용하였다. 해쉬함수를 자료구조에서 배웠었지만 문제 풀기는 어려웠고 많이 배워가는 시간이었다.