Count of Smaller Numbers After Self - LeetCode
오늘 Leetcode문제가 많이 어려웠다.
내가 아무리 생각해도 답이 안나오고 (bruteforce밖에 생각나지 않았다)
충분한 시간을 고민했기 때문에 다른사람의 solution을 봤다.
이 문제는 머지소트, 세그먼트 트리 등으로 풀 수 있지만
나에게 가장 직관적으로 와닿았던 것은 binary indexed tree (BIT) 또는 fenwick tree라고 불리는 자료구조를 이용한 풀이이다. (이제 이 자료구조를 BIT라고 하겠다)
일단 문제를 들어가기전에 BIT에 대해서 알아보자
BIT란?
BIT의 활용
일단 BIT는 부분합을 구할 때 쓰는 자료구조이다
그런데 단순히 부분합을 구할 때 쓰는게 아니라 배열합 구하기 - 배열의 값이 업데이트 이 두가지 상황이 교차해서 계속 나오는 경우 , 즉 단순히 배열합을 구하는 상황이 아니라 실시간으로 배열의 값이 바뀔 때 부분합을 구할 때 사용된다.
BIT소개
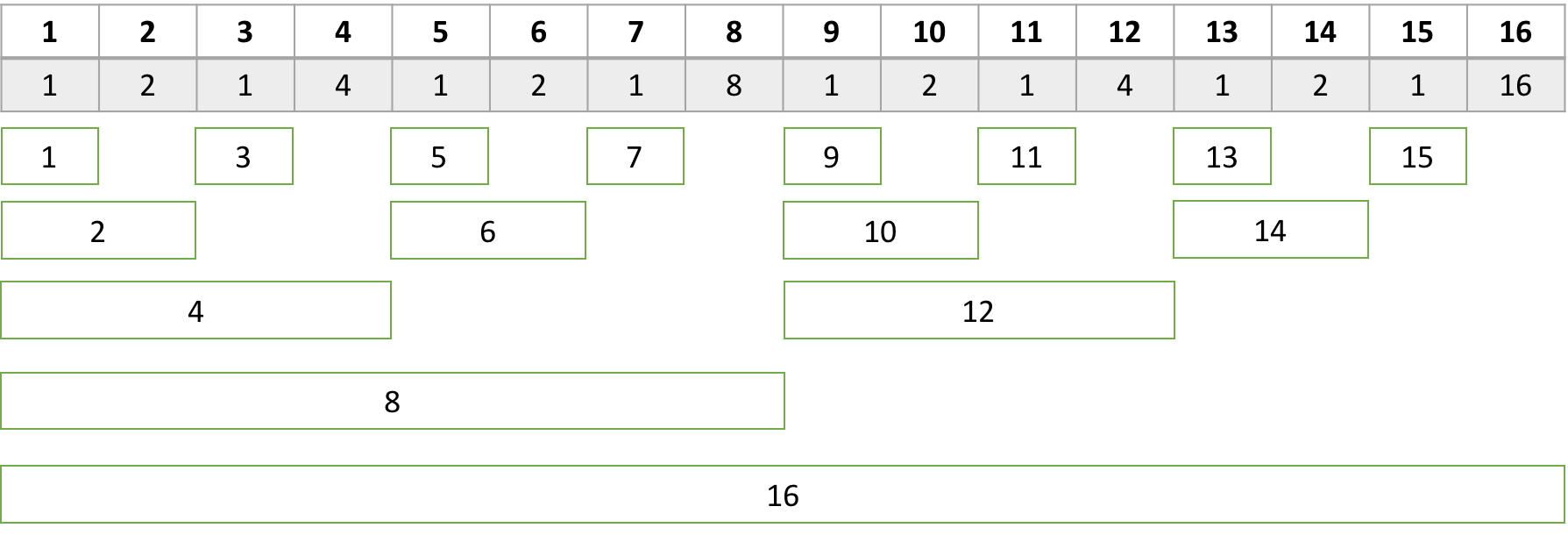
(자료출처:https://www.acmicpc.net/blog/view/21)
먼저 위의 그림을 보면 전혀 이해가 안될것이다.
이것을 이해하기 전에 먼저 알아둬야 할 사실이 있다 , 제일 마지막 1의 위치 (most significant non-zero bit)라는 것이다.
이것은 어떤 숫자를 2진수로 나타냈을 때 처음 1이 나타나는 위치를 말한다.
예를들어 10 ⇒ 1010 , 16 ⇒ 10000 과 같은데 각각 2, 16을 의미한다 할 수 있다.
이것을 구하는 방법은 간단하다.
어떤 숫자 num이 있으면 논리합 and를 -num과 해주면 된다.
이것은 2의 보수법과 관련이 있는데
이곳을 참조하면 일단 2의 보수법을 알 수 있을 것이다
예를들어 7같은 경우에 0000111 이고 , -7은 1111001이다 이것을 and 해주면 0000001 이다.
즉, num & -num을 해주면 제일 마지막 1의 위치의 값을 얻을 수 있다.
이제 다시 그림을 보자위 표를 보자. 하얀색 바탕의 숫자는 index를 의미하는 것이고 회색 숫자는 각 index마다 제일 마지막 1의 위치에 해당하는 값을 의미한다.
그리고 초록색은 , 초록색 상자에 있는 값이 가지고 있는 값의 범위를 의미한다
- 1은 A[1]의 값
- 2는 A[1]~A[2]의 누적합값
- 3은 A[3]의 값
- 4는 A[1]~A[4]의 누적합값
- 8은 A[1] ~ A[8]의 누적합값
이렇게 이해하면 된다.
예를들어 A= [3, 2, 5, 7, 10, 3, 2, 7, 8, 2, 1, 9, 5, 10, 7, 4] 일때 아래와 같다
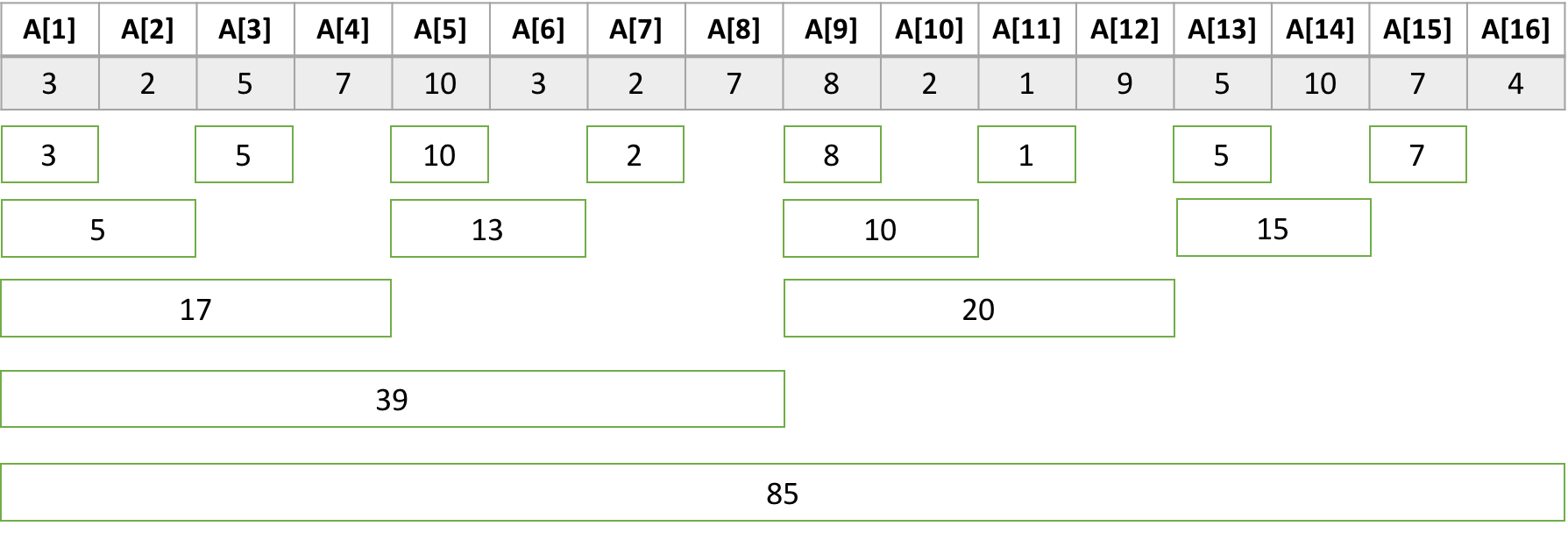
(출처:https://www.acmicpc.net/blog/view/21)
이제 BIT에 있는 operation 2가지를 알아보자
GetSum
n이 주어졌을 때 A[1]~A[n]까지의 합은 어떻게 구할 수 있을까?
예를들어 n이 11이라고 하면
A[1] + … +A[8] + A[9] + A[10] + A[11]인데
우리가 만든 BIT를 Tree라고 한다면
Tree[8]+Tree[10] + Tree[11]이라는 값이다.
우리가 어떤 숫자 k의 most significant non zero bit을 MSNZ(k)라고 하면
Tree[8]+Tree[10] + Tree[11] = Tree[11] + Tree[11-1] + Tree[10-2]
= Tree[11] + Tree[11-MSNZ(11)] + Tree[10-MSNZ(10)] 이 된다.
즉, n이 주어지면 Tree[n] 을 구하고 n= n - n&-n 을 해주고 다시 Tree[n]을 구하고를 n이 0이하가 될 때 까지 반복한다!
이것을 python code로 나타내면
def get_sum(i):
ret = 0
while i:
ret += Tree[i]
i -= i&-i
return ret이다
Update
그렇다면 값을 갱신해야할 때는 어떻게 할까?
예를들어 A[1]의 값이 바뀌면 영향을 받는 Tree의 값은 무엇일까?
Tree[1] , Tree[2] , Tree[4], Tree[8],Tree[16]이다
이미 위에서 GetSum한것과 뭔가 반대방향으로 흘러가는 느낌을 받았다면 그 느낌이 맞다
이것을 python code로 작성하면
def update(i,num):
while i<Tree_length:
Tree[i] += num
i += i&-i 이제 BIT에 대해서 배웠다. 이것을 어떻게 문제에 적용 시킬지는 다음 포스트에서 살펴보자
참고문헌
https://www.acmicpc.net/blog/view/21
https://www.youtube.com/watch?v=fg2iGP4e2mc
