🔍 2263 트리의 순회

n개의 정점을 갖는 이진 트리의 정점에 1부터 n까지의 번호가 중복 없이 매겨져 있다. 이와 같은 이진 트리의 인오더와 포스트오더가 주어졌을 때, 프리오더를 구하는 프로그램을 작성하시오.

---

🤔 풀이

• postorder, inorder의 특성을 이용하여 푼다.
  - postorder의 끝에 있는 노드를 뽑아 inorder에서 같은 노드를 찾았을 때, 그 좌우로는 left child, right child를 이룬다.
  • postorder에서 뽑은 노드의 앞부분을 left child의 수 / right child의 수로 각각 나누면 해당 노드들도 좌우자식 노드인 특성을 만족한다. (그림2의 노란부분 참고)
• 이런 트리가 존재한다고 하면, postorder, inorder와 preorder는 각각으로 나타낼 수 있다.
  
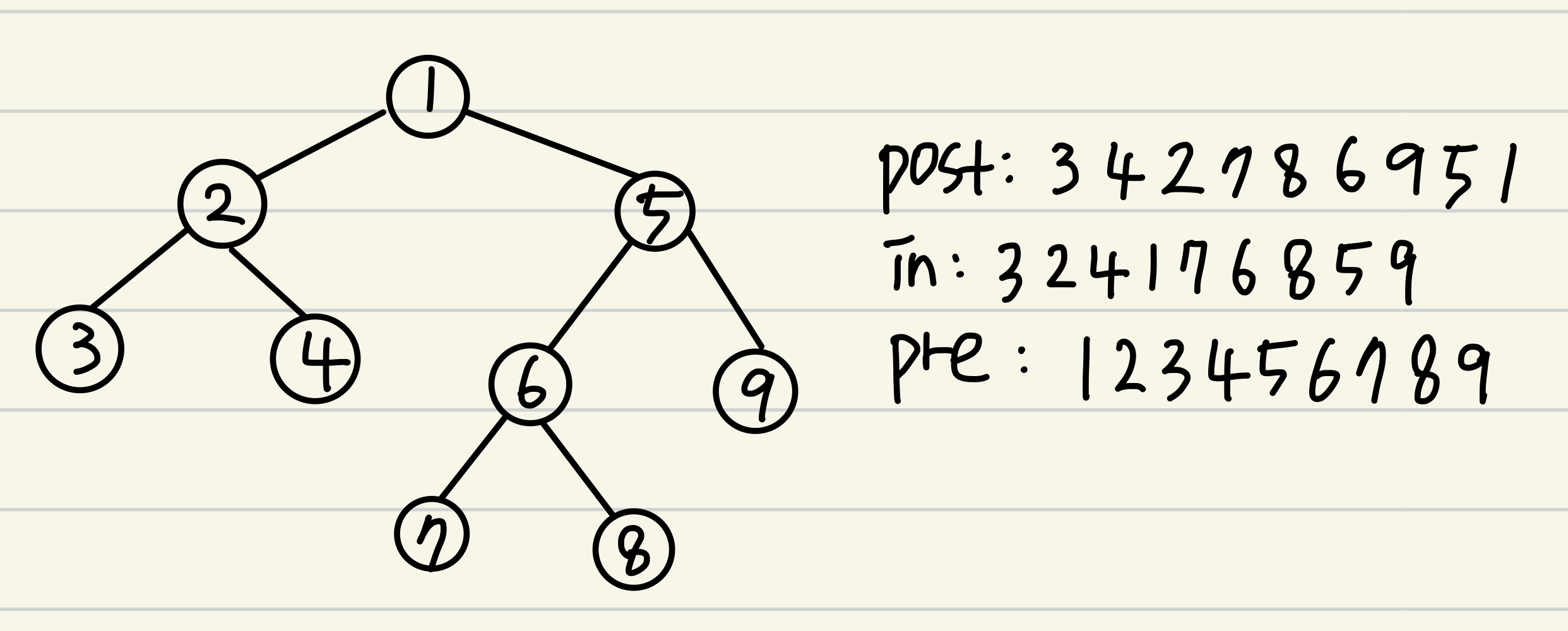
• 만약 postorder 끝의 노드₁을 뽑아 inorder에서 찾는다. inorder의 노드₁ 좌우에는 해당 노드들이 있다. 왼쪽에 위치한 노드들은 노드₁의 왼쪽에 위치하고, 오른쪽에 있는 노드들은 노드₁의 오른쪽에 위치한다.
  - inorder에서 해당 값의 위치를 빨리 찾기 위해, arr[value] = index 인 배열을 하나 만들었다.
  
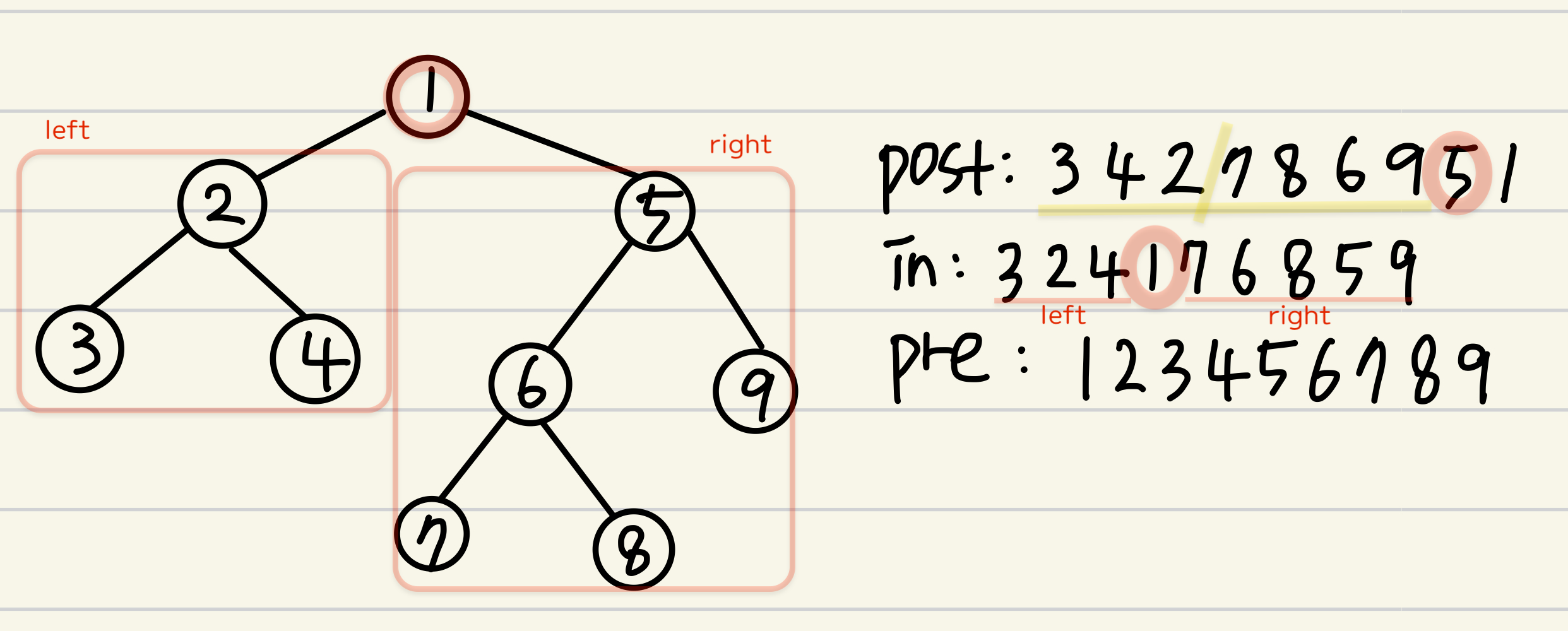
• postorder는 왼쪽-오른쪽-자신을 순서로 가진다. 따라서 맨 끝에서 '자신'노드인 노드₁을 뽑았기 때문에, postorder 끝의 바로 이전 노드는 노드₁의 오른쪽 노드가 된다.
• 이를 이용해 노드₁의 오른쪽 child tree의 루트 노드, 노드₅의 좌우 자식들을 구할 수 있다. (단, 해당 자식노드들도 노드₁의 오른쪽에 위치해야 하는것은 변함이 없다. 따라서 inorder의 탐색 범위를 노드₁의 오른쪽 자식들로 한다.)
  
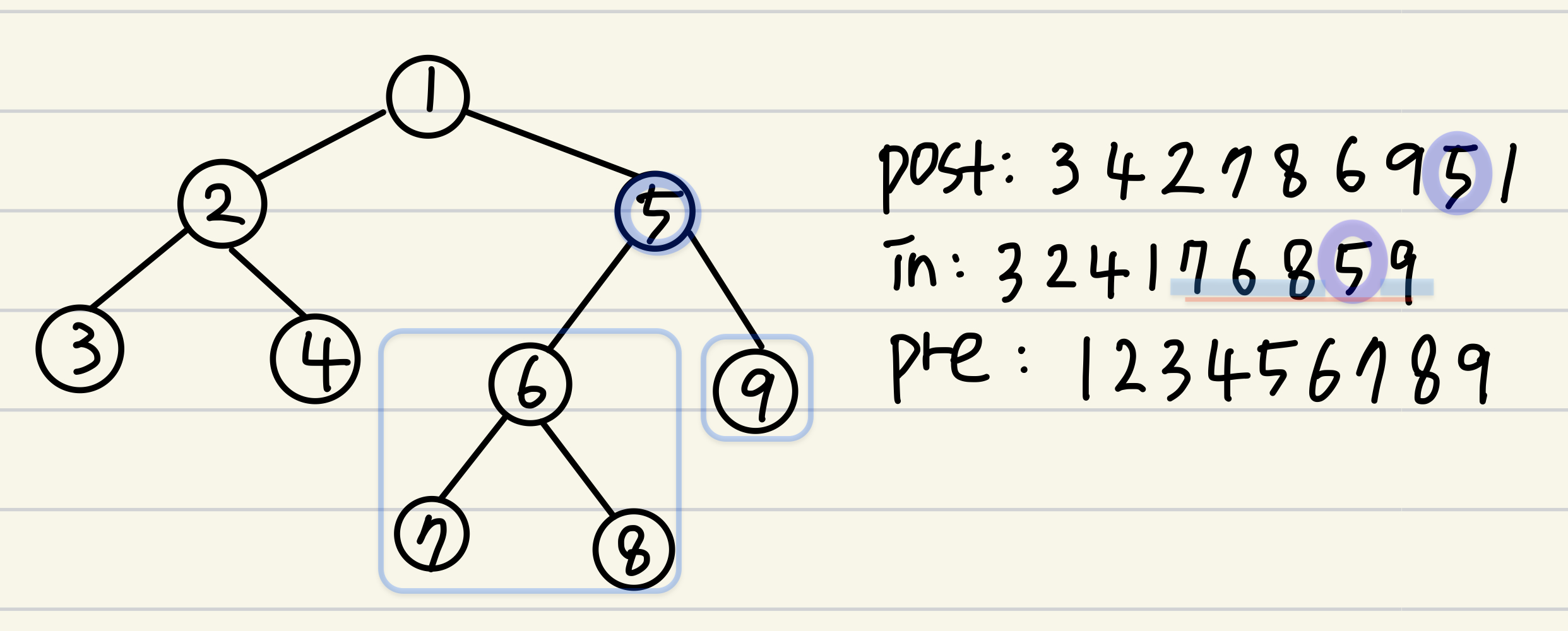
• 자기 자신의 자식 노드들이 없을 때까지 해당 방법을 반복하면 트리의 구조를 알아낼 수 있다. (작은 것으로 나눠 답을 구하는 분할정복). 다만 preorder는 자신-왼쪽-오른쪽 순이므로, 해당 순서를 참고해 postorder 탐색을 자신→왼쪽→오른쪽 순서로 하여 문제를 푼다.

---

📝 코드

#include <iostream>
using namespace std;

int n;
int inorder[100000];
int postorder[100000];
int find_idx_inorder[100001]; // +1

void divide(int inStart, int inEnd, int postStart, int postEnd) {
    if (inStart > inEnd || postStart > postEnd) return ;

    int in_root_idx = find_idx_inorder[postorder[postEnd]];
    int left_size = in_root_idx - inStart - 1;
    cout << inorder[in_root_idx] << " ";

    divide(inStart, in_root_idx-1, postStart, postStart+left_size);
    divide(in_root_idx+1, inEnd, postStart+left_size+1, postEnd-1);
}

int main() {
    ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> inorder[i];
        find_idx_inorder[inorder[i]] = i;
    }
    for (int i = 0; i < n; i++) {
        cin >> postorder[i];
    }

    divide(0, n-1, 0, n-1);

    return 0;
}