🔍 13549 숨바꼭질 3

수빈이는 동생과 숨바꼭질을 하고 있다. 수빈이는 현재 점 N(0 ≤ N ≤ 100,000)에 있고, 동생은 점 K(0 ≤ K ≤ 100,000)에 있다. 수빈이는 걷거나 순간이동을 할 수 있다. 만약, 수빈이의 위치가 X일 때 걷는다면 1초 후에 X-1 또는 X+1로 이동하게 된다. 순간이동을 하는 경우에는 0초 후에 2*X의 위치로 이동하게 된다.

수빈이와 동생의 위치가 주어졌을 때, 수빈이가 동생을 찾을 수 있는 가장 빠른 시간이 몇 초 후인지 구하는 프로그램을 작성하시오.

---

🤔 풀이1 - DP

• 수빈이가 $X$에 있을 때 갈 수 있는 위치는 $X-1, X+1, 2\times X$ 이다.
  반대로 수빈이가 $X$위치에 있을 땐, $X+1$에서 -1로 걸어서 오거나 $X-1$에서 +1로 걸어서 오거나 또는 $X/2$에서 순간이동을 하는 방법이 있다. (X/2가 정수일 때만)
• 따라서 $DP[X] = min(DP[X-1], DP[X+1], DP[X/2])$ 식을 구할 수 있다.
  다만, 현재 수빈이의 위치보다 작은 경우에는 -1로 걸어서가는 방법밖에 없으므로 그 부분은 앞서 따로 계산한다.
• 추가적으로, 순간이동 방식은 비용이 들지 않으므로 방금 구한 X의 2배수가 되는 모든 좌표값에 미리 계산해둔다.

---

📝 코드1

#include <iostream>
#define INF 987654321
#define MAX 100002
using namespace std;

int N, K;
int memo[MAX];

int main() {
    cin >> N >> K;

    for (int i = 0; i < MAX; i++) {
        memo[i] = INF;
    }
    memo[0] = N;

    for (int i = 1; i < MAX; i++) {
        // N보다 작은 경우를 구하는 DP,
        if (i < N) {
            memo[i] = N - i;
        }
        // N보다 큰 경우를 구하는 DP.
        // n = k_1 + 1, n = k_2 - 1, n = k_3 * 2 => k1 = n-1, k2 = n+1, k3 = n/2
        else if (i == N) memo[i] = 0;
        else {
            if (i%2 == 0) {
                memo[i] = min(min(memo[i+1]+1, memo[i-1]+1), memo[i/2]);
            }
            else {
                memo[i] = min(memo[i+1]+1, memo[i-1]+1);
            }
        }
        int idx = i*2;
        while (idx < MAX) {
            memo[idx] = min(memo[idx], memo[i]);
            idx = idx*2;
        }
    }

    cout << memo[K];

    return 0;
}

---

🤔 풀이2 - 다익스트라

도착지점	비용
$N-1$	1
$N+1$	1
$2N$	0

• 만약 위치들을 하나의 노드로 본다면, 한 $N$ 노드에서 다른 노드로 갈 수 있는 경로와 비용은 위와 같다. 따라서 만약 0~5까지의 좌표만 존재하는 세계라면 경로를 다음과 같은 그래프로 나타낼 수 있다.
  
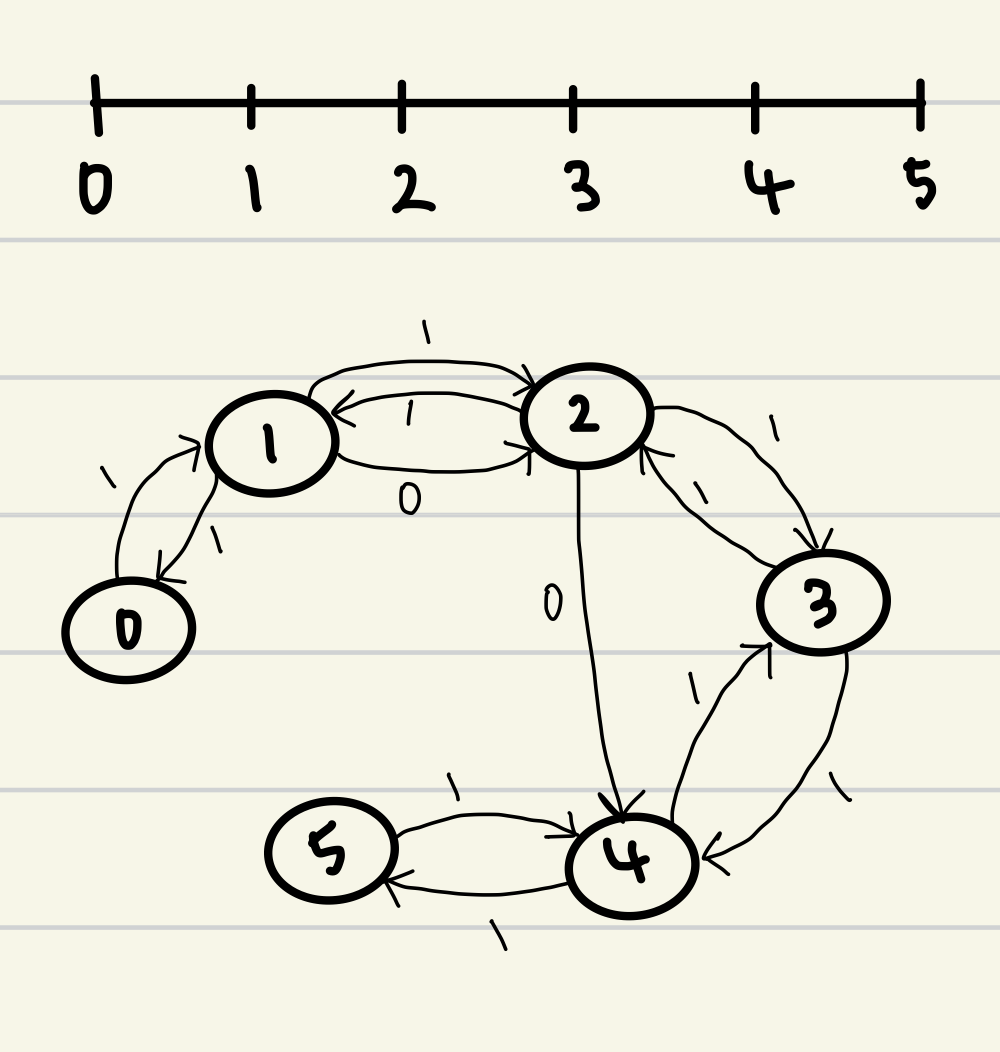
• 어디서 많이 본 그래프.. 경로와 비용을 아는 상태이니 다익스트라 알고리즘으로 풀어본다.
• 수빈이의 현재 점을 기준으로 노드 지점간의 최소비용을 다 계산한다.
  - 입력받게 되는 좌표의 최대가 100001이므로 앞선 방법보다 계산시간이 더 걸리게 된다.
• 동생의 위치와 입력받은 수빈이의 현재 위치까지 갈 수 있는 최소비용이 담긴 d[K]를 출력하면 답이 된다.

---

📝 코드2

#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#define MAX 100001
using namespace std;

int N, K;
int d[MAX];

int isRange(int node) { return node >= 0 && node < MAX; }

void dijk() {
    priority_queue<pair<int, int> > que;
    fill(d, d+MAX, -1);
    d[N] = 0;
    que.push(make_pair(0, N));

    int near_cost[3] = {1, 1, 0};
    int near_node[3];
    while (!que.empty()) {
        int top_node = que.top().second; int top_cost = -que.top().first;
        que.pop();

        if (d[top_node] < top_cost) continue;
        
        near_node[0] = top_node-1; near_node[1] = top_node+1; near_node[2] = top_node*2; 
        
        for (int i = 0; i < 3; i++) {
            if (isRange(near_node[i])) {
                if (d[near_node[i]] > top_cost + near_cost[i] || d[near_node[i]] == -1) {
                    d[near_node[i]] = top_cost+near_cost[i];
                    que.push(make_pair(-d[near_node[i]], near_node[i]));
                }
            }
        }
    }
}

int main() {
    cin >> N >> K;

    dijk();
    cout << d[K];

    return 0;
}