[U] Week 1 Day 4

이동찬·2022년 10월 1일

ai math 네이버 부스트캠프 AI Tech 4기

네이버 부스트캠프 AI Tech

목록 보기

5/18

1. 강의 복습 내용

< AI Math >

(1) 벡터가 뭔가요?

벡터 : 숫자를 원소로 가지는 리스트(list) or 배열(array)
- 공간에서 "하나의 점"을 나타냄
- 원점으로부터 "상대적 위치"를 표현
벡터에 스칼라곱 : 길이만 변함 (스칼라값이 0보다 작으면 반대 방향)
성분곱(Hadamard product; element-wise product)
두 벡터의 덧셈 : 다른 벡터로부터 상대적 위치 이동을 표현
- 뺄셈 = 방향을 뒤집은 덧셈
노름(norm) : 원점에서부터의 거리를 의미, 벡터의 크기를 표현
- L1-norm : 각 성분의 변화량의 절댓값을 더한 것으로 표현 (Robust 학습, Lasso 회귀에서 사용)
  $||x||_1$ = $\sum_{i=1}^{d} |x_i|$
```
import numpy as np

def l1_norm(x):
    x_norm = np.abs(x)
    x_norm = np.sum(x_norm)
    return x_norm
```
- L2-norm : 피타고라스 정리를 이용해 유클리드 거리를 계산 (Ridge 회귀, Laplace 근사에서 사용)
  - 각 원소들의 제곱의 합을 제곱근 해준 것으로 표현
  - 이상치에 민감
  $||x||_2$ = $\sqrt{\sum_{i=1}^{d} {x_i}^2}$ = $\sqrt{x^Tx}$
```
import numpy as np

def l2_norm(x):
    x_norm = np.sum(x * x)
    x_norm = np.sqrt(x_norm)
    return x_norm
    
def l2_norm(x):
	return np.linalg.norm(x)
```
- 노름의 종류에 따라 기하학적 성질이 달라짐

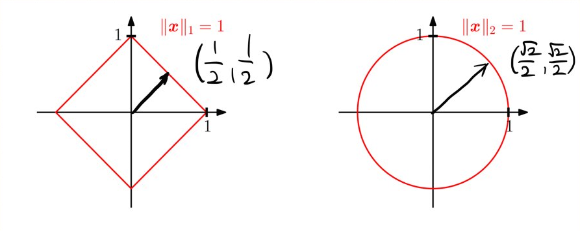
두 벡터 사이의 거리를 계산할 때,
- L1, L2 norm을 이용, 벡터의 뺄셈을 이용
- $||y - x|| = ||x - y||$
두 벡터 사이의 거리를 이용하여 각도 구하기 (주의 : L2-norm만 가능)
- 제 2코사인 법칙 : $a^2 = b^2+c^2-2bc\cos{A}$
- $\cos{\theta}$ = $<x,y> \over{||x||_2||y||_2}$
→ 내적(inner product; dot product; 행렬곱) : $<x,y>$ = $\sum_{i=1}^{d} x_iy_i$

def angle(x, y):  # cos⍬
	v = np.inner(x, y) / (l2_norm(x) * l2_norm(y))  # 내적 : np.inner()로 계산
    theta = np.arccos(v)  # 역코사인
    return theta

내적 : 정사영(orthogonal projection)된 벡터의 길이
두 벡터의 유사도(similarity)를 측정할 때 내적을 이용
→ 두 벡터가 얼마나 비슷한 방향으로 가고 있는지 측정

(2) 행렬이 뭔가요?

행렬(matrix) : 행 벡터를 원소로 가지는 2차원 배열 ( $X$ = ( $x_{ij}$ ))
벡터가 공간에서 한 점을 의미한다면, 행렬은 여러 점들을 나타냄
행렬 곱셈(matrix multiplication) : i번째 행 벡터와 j번째 열 벡터 사이의 내적을 성분으로 가지는 행렬을 계산
$XY = (\sum_k x_{ik}y_{kj})$
→ X의 열의 개수와 Y의 행의 개수가 같아야 함

X @ Y  # 행렬 곱 : numpy에서는 @ 연산을 이용

np.inner() : i번째 행 벡터와 j번째 행 벡터 사이의 내적을 성분으로 가지는 행렬 계산
→ 행렬 곱 : X @ Y == np.inner(X, np.transpose(Y))
행렬 곱
→ 벡터를 다른 차원의 공간으로 보낼 수 있음
→ 패턴을 추출하거나 데이터를 압축할 수 있음
→ 모든 선형 변환(linear transform)은 행렬 곱으로 계산할 수 있음
역행렬(inverse matrix) : 행과 열 숫자가 같고, 행렬식(determinant)이 0이 아닌 경우에만 계산 가능

X = np.array([[1, -2, 3], 
			  [7, 5, 0],
              [-2, -1, 2]])

X @ np.linalg.inv(X)  # X와 X의 역행렬을 곱하면 항등행렬(identity matrix)

역행렬을 계산할 수 없다면, 유사역행렬(pseudo-inverse) or 무어-펜로즈(Moore-Penrose) 역행렬 $A^+$ 이용
→ 행과 열의 개수가 달라도 사용 가능
- 행의 개수 n, 열의 개수 m일 때,
  - n ≥ m인 경우, $A^+ = (A^TA)^{-1}A^T$
    → $(A^+A = I)$
    n ≤ m인 경우, $A^+ = A^T(AA^T)^{-1}$
    → $(AA^+ = I)$

X = np.array([[0, 1], 
			  [1, -1],
              [-2, 1]])

np.linalg.pinv(X) @ X  # n ≥ m이므로, X의 유사역행렬(pseudo-inverse)과 X를 곱하면 항등행렬

응용 1 : 연립방정식 풀기(n ≤ m인 경우)

식의 개수 n이 변수의 개수 m보다 작거나 같을 때, 무어-펜로즈 역행렬을 이용하여 연립방정식을 만족하는 해 $x_j$ 를 하나 구할 수 있음

응용 2 : 선형회귀분석(n ≥ m인 경우)

데이터가 변수 개수보다 많거나 같을 때, 계수 $\beta$ 를 근사하여 구할 수 있음
데이터를 선형모델(linear model)로 해석하는 선형회귀식을 찾을 수 있음
- $X\beta = y$ 에서 계수 $\beta$ 찾기
→ 연립방정식과 달리 행의 개수 n이 더 크므로 방정식을 푸는 것은 불가능 (해를 구할 수는 X)
→ 선형회귀분석 : 더 많은 데이터를 "최대한 근사할 수 있는 계수 $\beta$ "를 찾아 $X\beta$ 를 그리는 게 목적
- 무어-펜로즈 역행렬을 이용하여 L2-norm을 최소화하는 $\beta$ 와 예측값 $\hat{y}$ 찾기
  → min( $\beta)$ $||y - \hat{y}||_2$

(3) 경사하강법 (순한맛)

미분(differentiation) : 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구로 최적화에서 제일 많이 사용하는 기법
→ 미분은 변화율(=기울기)의 극한(limit)으로 정의
$f'(x) = \displaystyle \lim_{h \to 0}\frac{f(x+h) - f(x)}{h}$

import sympy as sym
from sympy.abc import x

sym.diff(sym.poly(x**2 + 2*x + 3), x)  # sympy : symbolic python, poly : polynomial(다항식)

>>> Poly(2*x + 2, x, domain='ZZ')

한 점에서 접선의 기울기를 알면 어느 방향으로 점을 움직여야 함수값이 증가하는지/감소하는지 알 수 있음
→ 함수값( $f(x)$ )을 증가시키려면, 미분값 더하기( $x=x + f'(x)$ ) :
경사상승법(gradient ascent), 목적함수 최대화
→ 함수값( $f(x)$ )을 감소시키려면, 미분값 빼기( $x=x - f'(x)$ ) :
경사하강법(gradient descent), 목적함수 최소화

# 경사하강법 알고리즘 pseudo-code
# Input : gradient(미분 계산 함수), init(시작점), lr(학습률), eps(알고리즘 종료 조건)
# Output : var
var = init
grad = gradient(var)

while (abs(grad) > eps):  # 컴퓨터로 계산할 때, 미분이 정확히 0이 될 수 없으므로 eps보다 작을 때 종료하는 조건
	var = var - lr * grad
    grad = gradient(var)  # 미분값 업데이트

벡터가 입력인 다변수 함수의 경우 편미분(partial differentiation)을 사용
→ $i$ 번째 방향에서의 변화율 계산
$\partial_{x_i}f(x) = \displaystyle \lim_{h \to 0}\frac{f(x + he_i) - f(x)}{h}$
→ $e_i$ 는 $i$ 번째 값만 1이고 나머지는 0인 단위벡터
⇒ 즉, $x$ 벡터의 $i$ 번째 항에만 영향을 줌
각 변수별로 편미분을 계산한 그레디언트 벡터(gradient vector)를 이용하여 경사하강/경사상승법에 사용
$\nabla{f} = (\partial_{x_1}f, \partial_{x_2}f, ..., \partial_{x_d}f)$
→ $\nabla$ : $nabla$ (다변수를 입력으로 가지는 함수의 그레디언트 벡터를 표시하는 기호)
⇒ $f'(x)$ 대신 벡터 $\nabla{f}$ 를 사용하여 변수 $x=(x_1, ..., x_d)$ 를 동시에 업데이트

# 그레디언트 벡터를 이용한 경사하강법 알고리즘 pseudo-code
# Input : gradient(그레디언트 벡터 계산 함수), init(시작점), lr(학습률), eps(알고리즘 종료 조건)
# Output : var
var = init
grad = gradient(var)

while (norm(grad) > eps):  # 벡터는 절대값 대신 노름(norm)을 계산해서 종료 조건 설정
	var = var - lr * grad
    grad = gradient(var)

(4) 경사하강법 (매운맛)

(5) 딥러닝 학습방법 이해하기

비선형 모델인 신경망(neural network)

2. 피어 세션

각자가 학습 정리한 블로그 공유
→ velog, notion, jupyter notebook, github.io 등 팀원 각각이 다양한 플랫폼에서의 학습 정리
수식을 정리할 수 있는 LaTeX 문법 사용 방법 공유
- LaTeX 문법으로 수식을 씁시다!
- 위키백과 LaTeX 문법
- 시각적으로 입력해서 LaTeX 문법으로 변환해주는 사이트
팀 회의록 저장소로 만들었던 그룹 노션 페이지의 용량 문제가 발생해 개인 노션 페이지에 share 기능으로 전환