[알고리즘] 동적 계획법

동적 계획법이란❓

• 복잡한 문제를 여러 개의 간단한 문제로 분리하여 문제의 답을 구하는 방법

  원리와 구현 방식

  1. 동적 계획법으로 풀 수 있는지 확인하기

  큰 문제를 작은 문제로 나눌 수 있어야 한다.
  작은 문제들이 반복해서 사용되고 결과값은 항상 같아야 한다.

  2. 점화식 세우기

  논리적으로 전체 문제를 나누고, 전체 문제와 부분 문제 간의 인과 관계를 파악해야 한다.

  3. 메모이제이션 원리 이해하기

  모든 작은 문제들은 한 번만 계산해 DP 테이블에 저장해서 추후 문제를 풀 때 재사용한다.
  톱-다운 방식과 바텀-업 방식으로 구현할 수 있다.

  📝 문제 예시

  피보나치 수열 공식
  D[N] = D[N-1]+D[N-2] // N번째 수열 = N - 1번째 수열 + N - 2번째 수열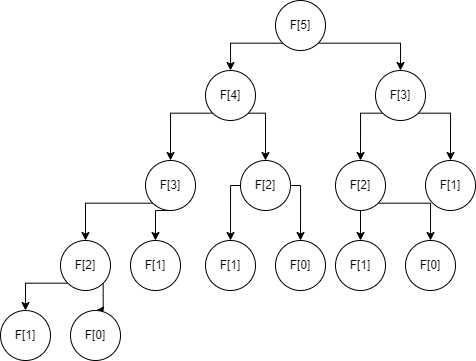

  

  DP 구현 방식1 - 톱-다운 방식 이해하기

• 말 그대로 위에서부터 문제를 파악해 내려오는 방식으로, 재귀 함수 형태로 구현

  public class P2747_TopDown{
   static int[] D;
   public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);
    int n = sc.nextInt();
    D = new int[n+1];
    for (int i =0; i<=n; i++) {
      D[i] = -1;
    }
    D[0] = 0;
    D[1] = 1;
    fibo(n);
    System.out.println(D[n]);
   }
   >
   statin int fibo(int n) {
    if (D[n] != -1)
      return D[n];
    return D[n] = fibo(n-2) + fibo(n-1);
   }
  }
  

DP 구현 방식2 - 바텀-업 구현 방식 이해하기

• 가장 작은 부분문제부터 문제를 해결 후 큰 문제를 푸는 방식이고 주로 반복문 형태이다.

public class P2747_TopDown{
   static int[] D;
   public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);
    int n = sc.nextInt();
    D = new int[n+1];
    for (int i =0; i<=n; i++) {
      D[i] = -1;
    }
    D[0] = 0;
    D[1] = 1;
    for (int i =2; i<=n; i++) {
     D[i] = D[i-1] + D[i-2];
    }
    System.out.println(D[n]);
   }
 }

문제 예시 2 - 정수를 1로 만들기 (백준 온라인 저지 1463번)

📝 문제 설명

정수 X에 사용할 수 있는 연산은 다음 3가지다.
1. X가 3으로 나누어떨어지면 3으로 나눈다.
2. X가 2로 나누어떨어지면 2로 나눈다.
3. 1을 뺀다.

정수 N이 주어졌을 때 위와 같은 연산 3개를 적절히 사용해 1을 만들려고 한다. 연산을 사용하는 횟수의 최솟값을 출력하시오.

🖊️ 입력

1번째 줄에 1보다 크거나 같고, 106보다 작거나 같은 정수 N이 주어진다.

출력

1번째 출에 연산을 하는 횟수의 최솟값을 출력한다.

입력	출력
10	3
2	1

문제 풀이

점화식 구하기

D[i] = D[i-1] +1 // 1을 빼는 연산이 가능할 때
if( i% 2 == 0) D[i] = min(D[i], D[i/2] +1) // 2로 나누는 연산이 가능할 때
if ( i% 3 ==0) D[i] = min(D[i], D[i/3] +1) //3으로 나누는 연산이 가능할 때

public class P1463_1로만들기 {
 static int N;
 static int D[];
 public static void main(String[] args) throws Exception {
  Scanner sc = new Scanner(System.in);
  N= sc.nextInt();
  D = new int[N+1];
  D[1] = 0;
  for (int i =2; i <=N; i++) {
   D[i] = D[i-1] +1;
   if( i% 2 == 0) D[i] = min(D[i], D[i/2] +1);
   if ( i% 3 ==0) D[i] = min(D[i], D[i/3] +1);
  }
  System.out.println(D[N]);
 }
}

참고

• 알고리즘 코딩테스트 (자바편) - 김종관