시행과 사건
시행
시행 (Trial)
동일한 조건 아래서 반복할 수 있으며, 그 결과가 우연에 의해 달라질 수 있는 실험 또는 관찰
독립 시행 (Independent Trial)
동일한 조건 아래서 어떤 시행을 반복할 때, 각 시행의 결과가 이전 시행의 결과에 영향을 받지 않는 시행
복원 추출 (Replacement)
첫 번째 나온 바둑돌을 주머니 안에 다시 넣는 방법으로 주머니에서 바둑돌을 꺼내는 추출방
법
비복원 추출 (Without Replacement)
첫 번째 나온 바둑돌을 주머니 안에 다시 넣지 않는 방법으로 바둑돌을 꺼내는 추출방법
사건
표본공간 (Sample Space)과 원소 (Element)
어떤 시행 결과로 기록되거나 관찰될 수 있는 모든 결과들의 집합. 시행에서 나타날 수 있는
개개의 결과
사건 (Event)
표본공간의 부분집합
근원사건(Elementary event)과 공사건(Empty event)
단 하나의 원소로 구성된 사건. 원소가 하나도 들어있지 않은 사건
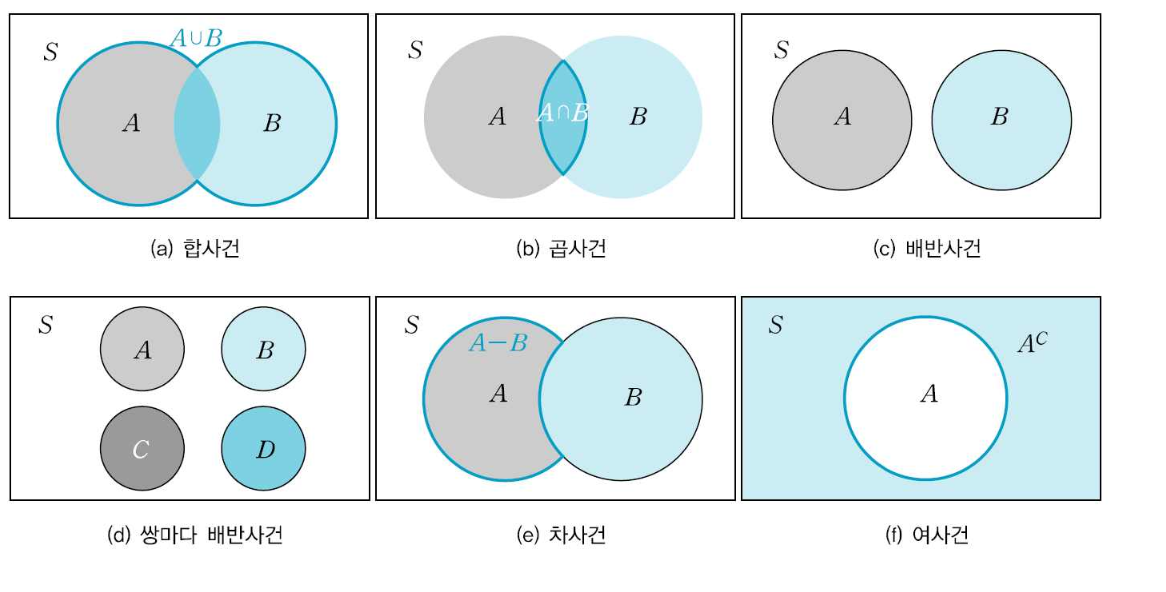
합사건 (Union)
A 또는 B 안에 있는 원소로 구성된 사건
A ∪ B = {ω| ω∈A 또는 ω∈B }
곱사건 (Intersection)
A 와 B 안에 있는 원소로 구성된 사건
A ∩ B = {ω| ω∈A 그리고 ω∈B }
서로 배반사건 (mutually exclusive events)
공통인 원소를 갖지 않는 두 사건 A와 B
A ∩ B=Φ
쌍마다 배반사건 (pair-wisely mutually exclusive events)
어느 두 사건도 공통인 원소를 갖지 않는 n개의 사건
A ∩ B=Φ, i≠j, i, j=1,2,…,n
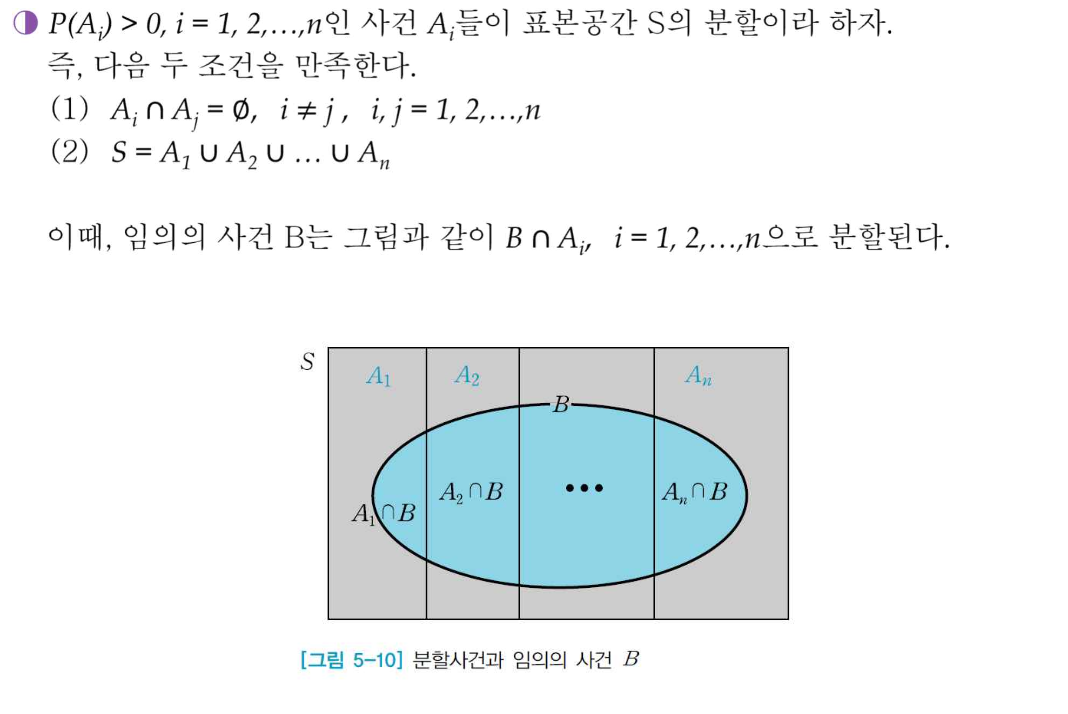
분할 (Partinion)쌍마다 배반이고, 합사건이 표본공간 S인 n개의 사건 A1, A2, ..., An
차사건 (Difference)
A 안에 있으나 B 안에 없는 원소로 구성된 사건
A - B = {ω| ω∈A 그리고 ω∉B }
여사건 (Complimentary)
Ac = {ω| ω∈S 그리고 ω∉A }
합사건의 성질

곱사건의 성질

여사건의 성질
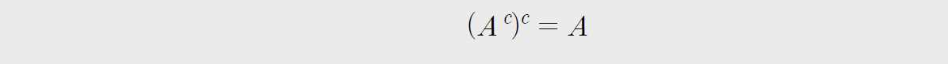
분배 법칙
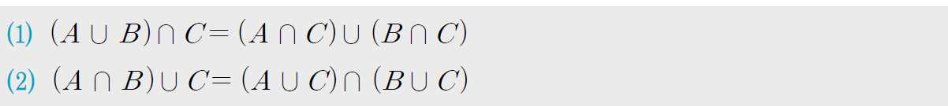
⭐️드모르간의 법칙

Let R = (A U B)' and S = A' ∩ B’.
R에 속하는 요소 y를 선택한다고 가정하면, y ∈ R로 표시된다. ⇒ y ∈ (A U B)'
⇒ y ∉ (A U B)
⇒ y ∉ A and y ∉ B
⇒ y ∈ A' and y ∈ B'
⇒ y ∈ A' ∩ B'
⇒y∈S
R = (A ∩ B)' and S = A' U B’
R에 속하는 요소 y를 선택한다고 가정하면, y ∈ R로 표시된다.
⇒ y ∈ (A ∩ B)'
⇒ y ∉ (A ∩ B)
⇒ y ∉ A' or y ∉ B'
⇒ y ∈ A' U B'
⇒y∈S
확률
확률의 성질
수학적 확률
어떤 시행에서 표본공간 S 안의 모든 원소가 일어날 가능성이 동등하다고 할 때, 사건 A가 일어날 확률은 다음과 같이 정의
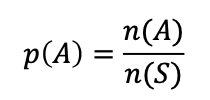
여기서 n(S)와 n(A)는 각각 표본공간 S와 사건 A 안에 들어있는 원소의 개수
통계적 확률

경험적 확률
어떤 시행을 A가 발생할 확률은 경험에 의해 정의됨

공리적 확률
다음 세 가지 공리를 만족하는 표본공간 S 에서 실수로 대응하는 함수 P(A) 를 사건 A 의 공리적 확률이라 함
1. P(S) = 1
2. A ⊂ S 이면 0 ≤ P(A) ≤ 1
3. 쌍마다 배반인 사건 An, n=1,2,3, ... 에 대해 다음이 성립함.
P(A1 ∪ A2 ∪ ...) = P(A1)+P(A2)+...
기하학적 확률P(A)는 표본공간 전체의 크기에 대한 도형 A의 크기
확률의 성질
기본 성질
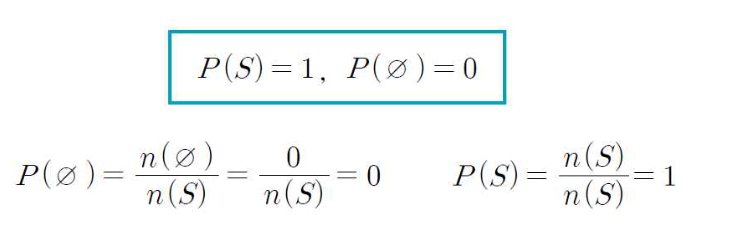
덧셈 법칙

여사건의 확률
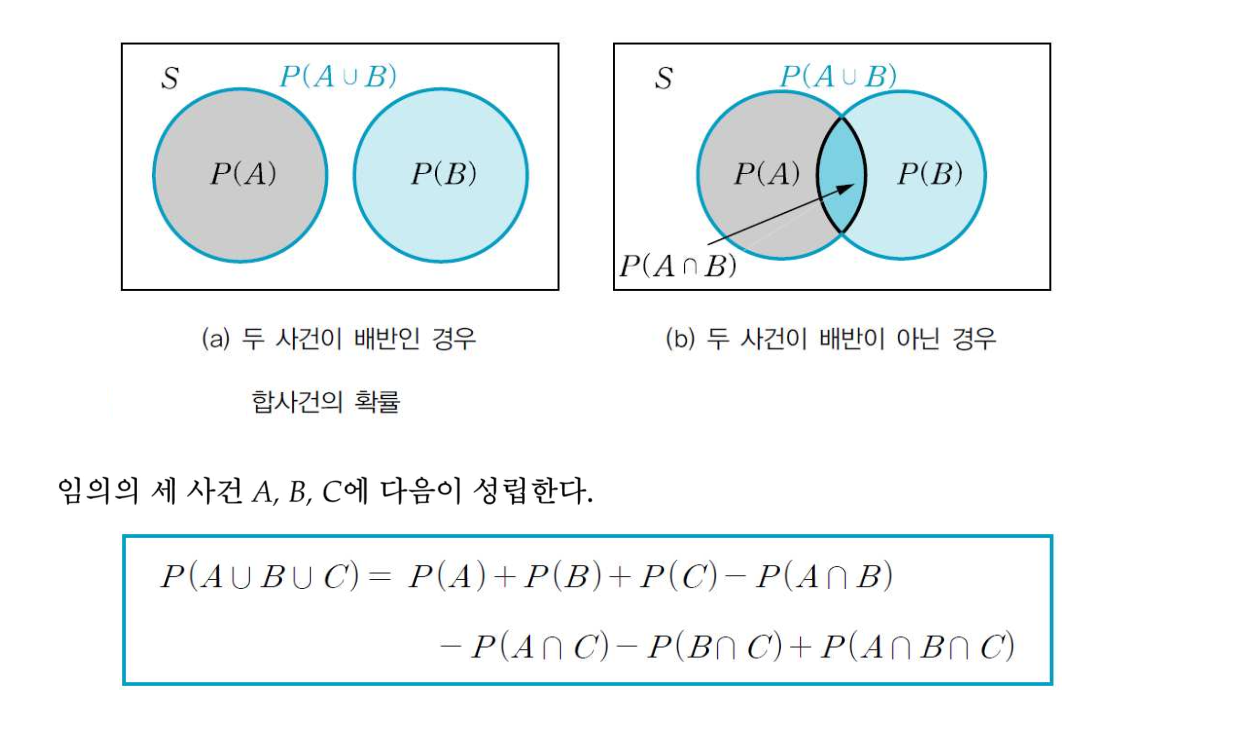
부분사건의 확률
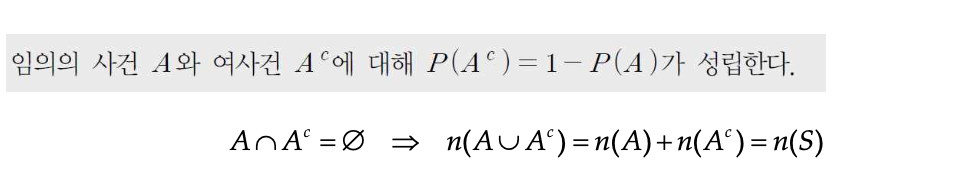
조건부 확률
조건부 확률
P(A) > 0 인 어떤 사건 A가 주어졌다고 할 때, 사전 B가 나타날 학률. P(B l A)로 표기
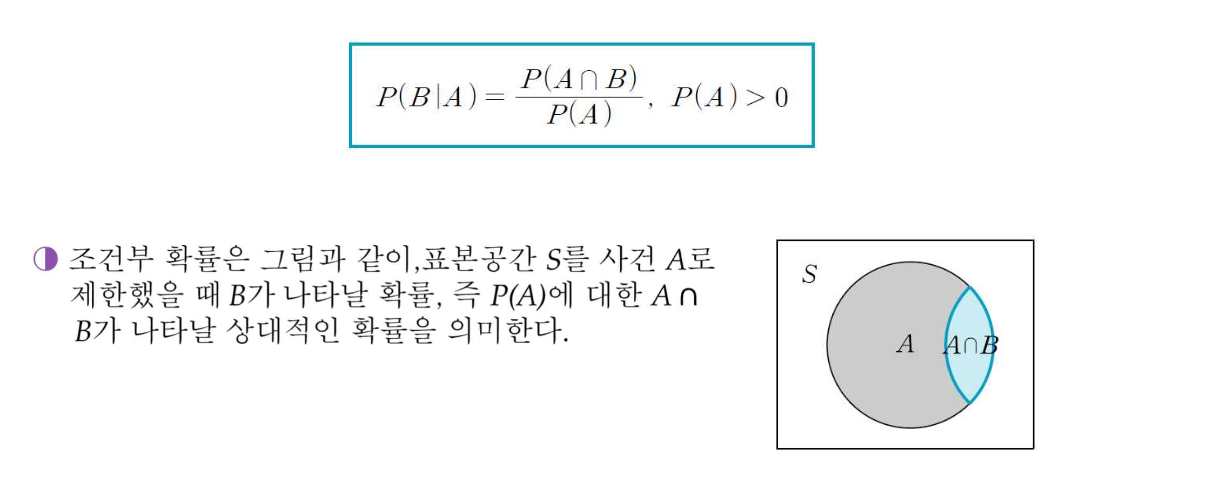
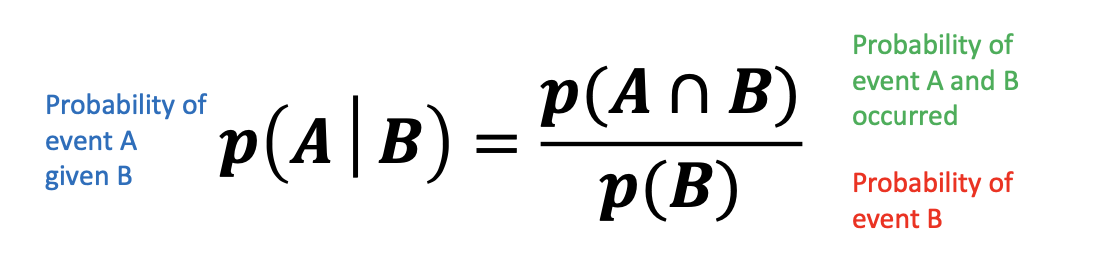

곱의 법칙

독립과 종속
독립 사건어느 한 사건의 발생 여부가 다른 사건이 일어날 확률에 영향을 주지 않는 두 사건 A와 B
종속 사건독립이 아닌 두 사건 A와 B

독립성

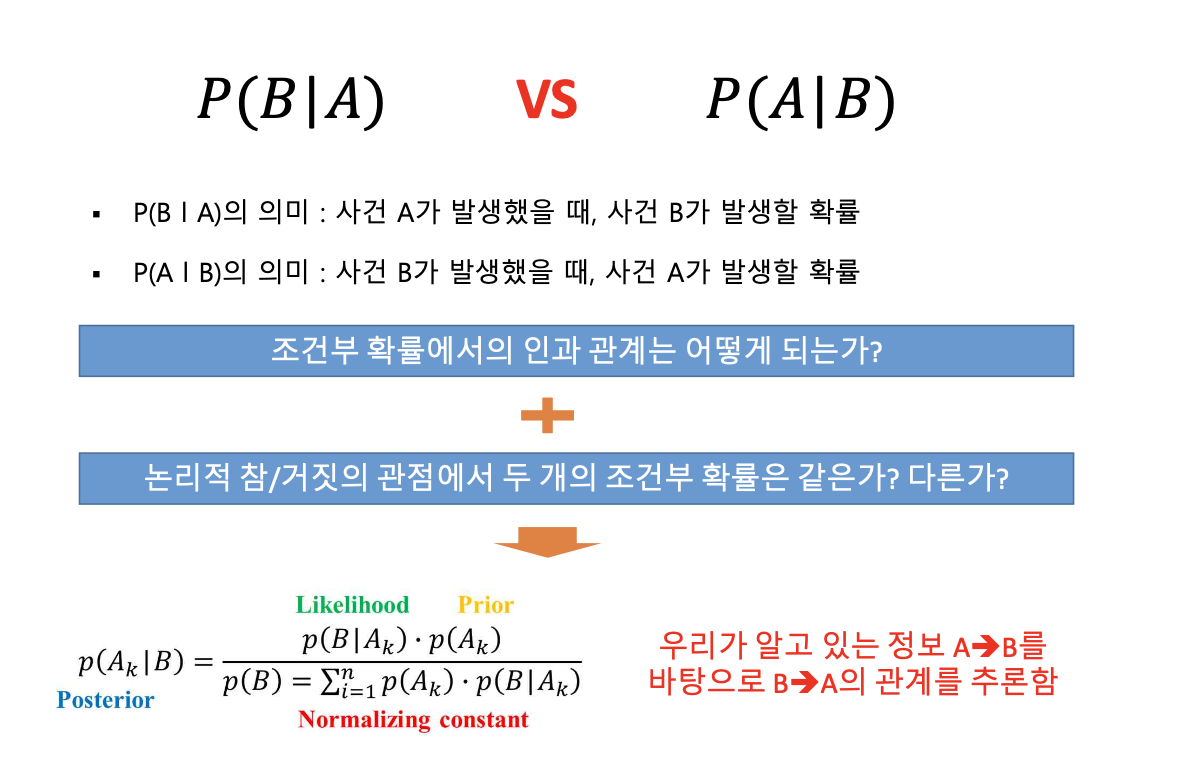
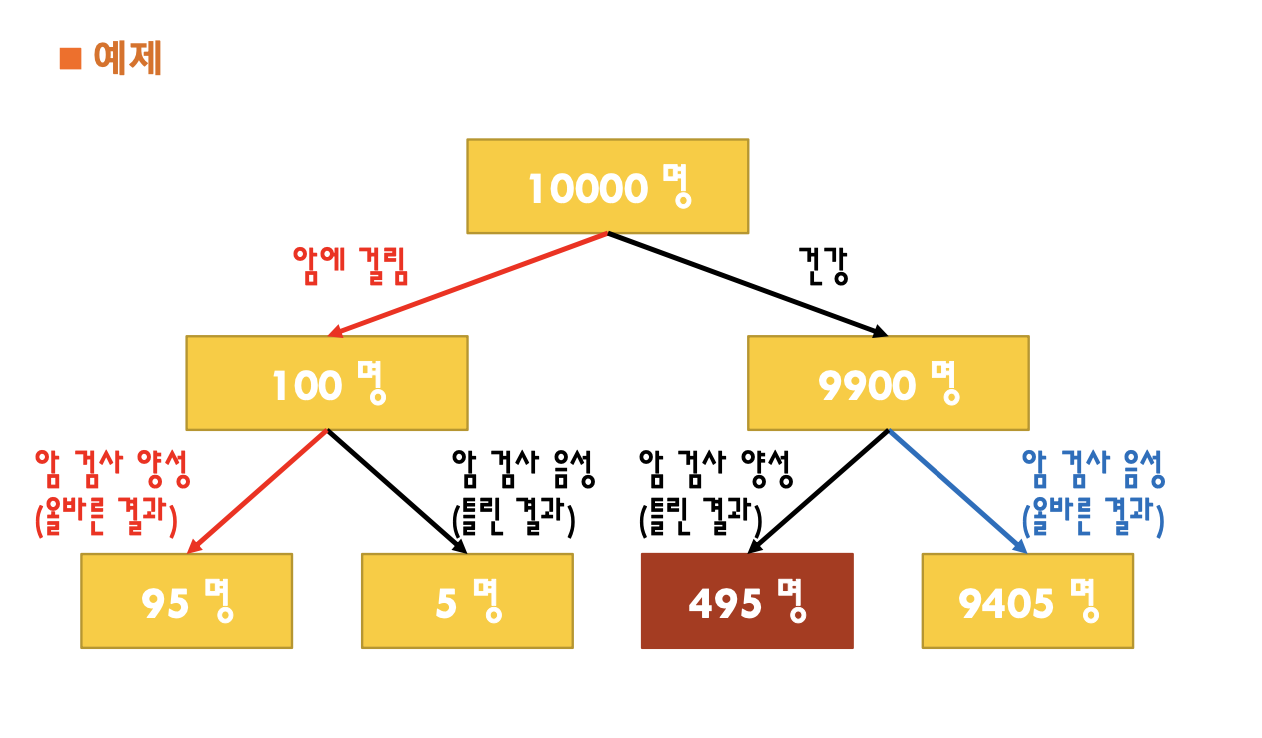
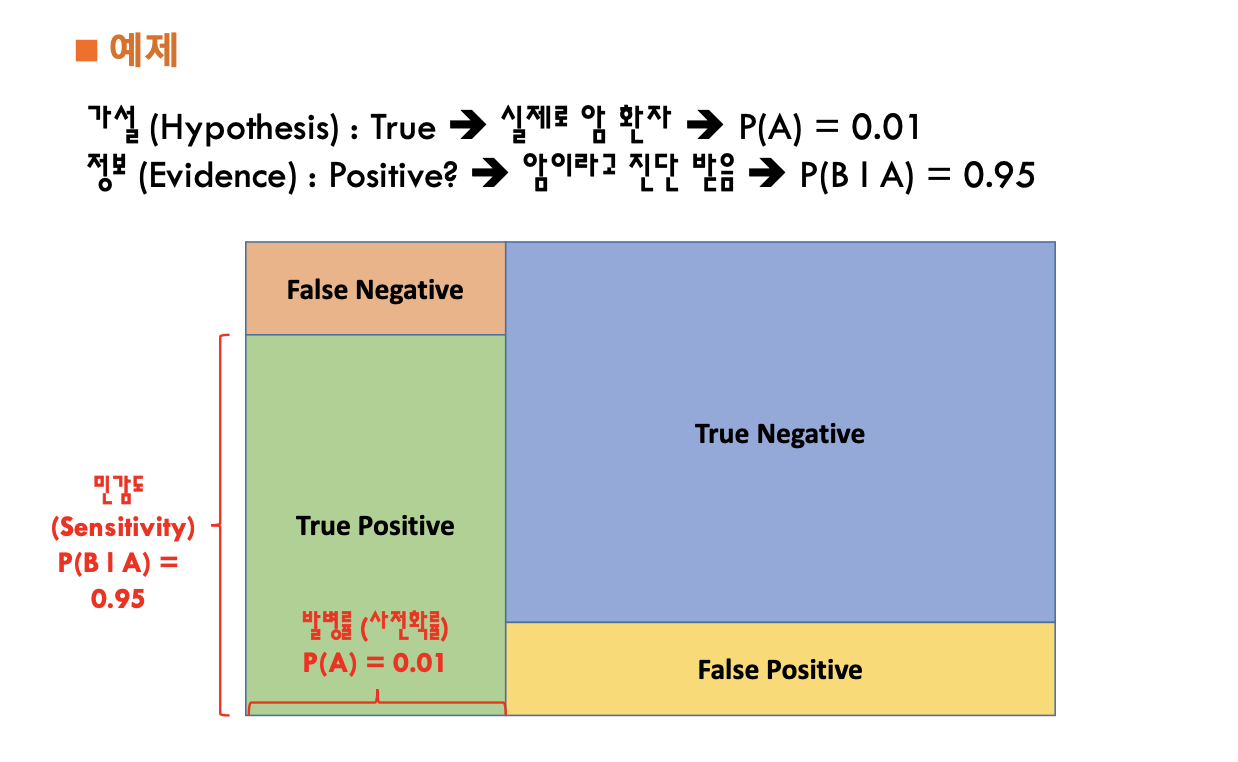
베이즈 정리
전환률 공식

베이즈정리