🗓️ 2023-01-02(월) ~ 2023-01-08(일)
KOALA 9기 코딩테스트반
🔍 완전탐색
완전탐색은 가능한 경우의 수를 모두 확인하여 원하는 답을 찾는 방법이다.
대부분의 알고리즘 문제는 시간 제한이 있어서, 입력의 개수(N)가 작을 때 사용하기 좋다.
⏳ 입력의 최대 크기 (1초)
O(N) : 1억
O(NlogN) : 500만
O(N^2) : 1만
O(N^3) : 500
O(2^N) : 20
O(N!) : 10🔐 문제를 풀 때
1. 시간 복잡도 계산
2. 이를 기반으로 완전탐색 vs 그 외 알고리즘 선택
Brute Force
반복문을 통해 가능한 모든 경우의 수를 단순하게 찾는 방법이다.
🪄 최소직사각형
function solution(sizes) {
const newSizes = sizes.map(x => x.sort((a, b) => a - b));
const minSize = Math.max(...newSizes.map(x => x[0]));
const maxSize = Math.max(...newSizes.map(x => x[1]));
return minSize * maxSize;
}🪄 모의고사
function solution(answers) {
const answer = [];
const mathGiver1 = [1, 2, 3, 4, 5];
const mathGiver2 = [2, 1, 2, 3, 2, 4, 2, 5];
const mathGiver3 = [3, 3, 1, 1, 2, 2, 4, 4, 5, 5];
const score1 = answers.filter((a, i) => a === mathGiver1[i % mathGiver1.length]).length;
const score2 = answers.filter((a, i) => a === mathGiver2[i % mathGiver2.length]).length;
const score3 = answers.filter((a, i) => a === mathGiver3[i % mathGiver3.length]).length;
const result = Math.max(score1, score2, score3);
if (score1 === result) {answer.push(1)};
if (score2 === result) {answer.push(2)};
if (score3 === result) {answer.push(3)};
return answer;
}재귀함수
재귀함수는 자기 자신을 호출하는 함수로, 사용하기 적합한 경우는 아래와 같다.
- 주어진 문제를 비슷한 구조의 더 작은 문제로 나눌 수 있는 경우
- 반복문으로 작성된 코드를 더욱 간결하고 이해하기 쉽게 작성하고 싶은 경우
🪄 JavaScript로 구현
function recursive(arr, num, ...) {
// base case : 문제를 더 이상 쪼갤 수 없는 경우
if (문제를 더 이상 쪼갤 수 없을 경우) {
return 문제의 해답;
}
// recursive case : 그렇지 않은 경우
for (재귀를 계속 진행할 범위) {
recursive(더 작은 문제로 새롭게 정의된 문제);
}
}🔐 문제를 풀 때
1. 재귀를 종료하기 위한 종료 조건이 필요하다.
2. 현재 함수의 상태를 저장하는 Parameter가 필요하다.
🔍 문제 유형
1. 피보나치 수열
2. 최대공약수 구하기 : 유클리드 호제법
3. 하노이탑
조합 / 순열
조합(nCr)
서로 다른 n개 중에 r개를 중복 없이 골라 "순서에 상관 없이" 나열하는 경우이다.
Input: [1, 2, 3]
Output: [[1, 2], [1, 3], [2, 3]]🔐 문제를 풀 때
1. 배열에서 선택하려는 개수를 확인한다.
2. 배열의 길이만큼 반복한다.
3. 배열에서 하나의 수를 선택한다. (기준 값)
4. 기준 값을 제외한 나머지 배열을 가지고 다시 1번부터 시작한다. (재귀)
🪄 JavaScript로 구현
const getCombinations = (arr, num) => {
const results = [];
// nC1 이며, 1이면 의미 없기때문에 바로 반환한다.
if (num === 1) return arr.map(v => [v]);
arr.forEach((fixed, index, origin) => {
// 조합에서는 값 순서에 상관없이 중복이 되면 안되기 때문에 현재값 이후의 배열들만 추출한다.
const rest = origin.slice(index + 1);
// 나머지 배열을 기준으로 다시 조합을 실시한다.
// 기준값(fixed)이 있기 때문에 선택하려는 개수에서 - 1 을 해준다.
const combinations = getCombinations(rest, num - 1);
// 기준값(fixed)에 돌아온 조합(combinations)을 붙인다.
const attached = combinations.map(v => [fixed, ...v]);
// 붙인 값을 결과 값에 넣어준다.
results.push(...attached);
});
return results;
}중복조합(nHr)
중복조합은 서로 다른 n개 중에 중복을 허용하여 r개를 골라 "순서에 상관 없이" 나열하는 경우이다.
(중복을 허용한다는건 기준점 숫자의 중복을 의미한다.)
Input: [1, 2, 3]
Output: [[1, 1], [1, 2], [1, 3], [2, 2], [2, 3], [3, 3]]🪄 JavaScript로 구현
const getRepeatCombinations = (arr, num) => {
const results = [];
// nH1 이며, 1이면 의미 없기때문에 바로 반환한다.
if (num === 1) return arr.map(v => [v]);
arr.forEach((fixed, index, origin) => {
// 중복 조합에서는 값 순서에 상관없이 중복이 가능하기 때문에 현재값을 포함한 배열을 추출한다.
const rest = origin.slice(index);
// 나머지 배열을 기준으로 다시 조합을 실시한다.
// 기준값(fixed)이 있기 때문에 선택하려는 개수에서 - 1 을 해준다.
const combinations = getRepeatCombinations(rest, num - 1);
// 기준값(fixed)에 돌아온 중복 조합(RepeatCombinations)을 붙인다.
const attached = combinations.map(v => [fixed, ...v]);
// 붙인 값을 결과 값에 넣어준다.
results.push(...attached);
});
return results;
}순열(nPr)
순열은 서로 다른 n개 중에 r개를 중복 없이 골라 "순서에 상관 있게" 나열하는 경우이다.
Input: [1, 2, 3]
Output: [[1, 2], [1, 3], [2, 1], [2, 3], [3, 1], [3, 2]]🔐 문제를 풀 때
1. 배열에서 선택하려는 개수를 확인한다.
2. 배열의 길이만큼 반복한다.
3. 배열에서 하나의 수를 선택한다. (기준 값)
4. 기준 값을 제외한 나머지 배열을 가지고 다시 1번부터 시작한다. (재귀)
🪄 JavaScript로 구현
const getPermutations = (arr, num) => {
const results = [];
// nP1 이며, 1이면 의미 없기때문에 바로 반환한다.
if (num === 1) return arr.map(v => [v]);
arr.forEach((fixed, index, origin) => {
// 순열에서는 조합과 달리 순서만 바뀌면 중복이 아니기때문에 기준값을 제외한 나머지 배열을 넣어준다.
const rest = [...origin.slice(0, index), ...origin.slice(index + 1)];
// 나머지 배열을 기준으로 다시 순열을 구한다.
// 기준값(fixed)이 있기 때문에 선택하려는 개수에서 - 1 을 해준다.
const permutations = getPermutations(rest, num - 1);
// 기준값(fixed)에 순열(permutations)을 붙인다.
const attached = permutations.map(v => [fixed, ...v]);
// 붙인 값을 결과 값에 넣어준다.
results.push(...attached);
});
return results;
}중복순열(nπr)
중복순열은 서로 다른 n개 중에 중복을 허용하여 r개를 골라 "순서에 상관 있게" 나열하는 경우이다.
(중복을 허용한다는건 기준점 숫자의 중복을 의미한다.)
Input: [1, 2, 3]
Output: [[1, 1], [1, 2], [1, 3], [2, 1], [2, 2], [2, 3], [3, 1], [3, 2], [3, 3]]🪄 JavaScript로 구현
const getRepeatPermutations = (arr, num) => {
const results = [];
if (num === 1) return arr.map(v => [v]);
arr.forEach((fixed, index, origin) => {
// 기준값(fixed)이 있기 때문에 선택하려는 개수에서 - 1 을 해준다.
const permutations = getRepeatPermutations(origin, num - 1);
// 기준값(fixed)에 순열(permutations)을 붙인다.
const attached = permutations.map(v => [fixed, ...v]);
// 붙인 값을 결과 값에 넣어준다.
results.push(...attached);
});
return results;
}Bitmask
TRUE/FALSE, ON/OFF 상태를 가진 배열을 이진수 표현하여 비트연산을 하는 방법이다.
AND ( & ) : 둘 다 1이면 1
OR ( | ) : 둘 중 1개만 1이면 1
XOR ( ^ ) : 서로 다를 때 1, 같으면 0
NOT ( ~ ) : 1이면 0, 0이면 1
SHIFT ( >>, << ) : A << B이면, A를 왼쪽으로 B 비트만큼 미는 것이다.🗝️ 사용하는 이유
1. 배열 활용만으로 해결할 수 없는 문제를 해결할 수 있다.
2. 적은 메모리와 빠른 수행시간으로 문제를 해결할 수 있다.
3. 코드가 간결해진다.
🪄 [1차] 비밀지도
function solution(n, arr1, arr2) {
let secretMap = [];
arr1.forEach((arr, idx) => {
secretMap.push(arr | arr2[idx]);
});
let decipherMap = [];
secretMap.map(secret => {
decipherMap.push(secret.toString(2).padStart(n, 0).replace(/1/gi, "#").replace(/0/gi, " "));
});
return decipherMap;
}Backtracking
답이 될 가능성이 없는 경로인 경우 되돌아가서(back) 다른 경로를 따라가는(tracking) 알고리즘 기법이다.
주로 DFS의 비효율적인 경로를 가지치기(Purning)하기 위해 사용된다.
DFS / BFS
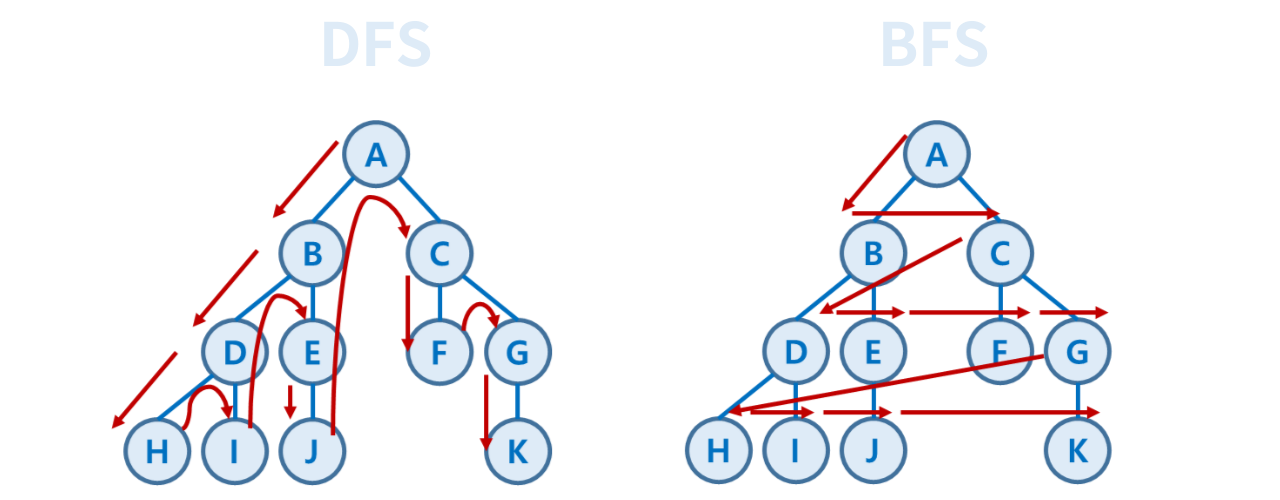
DFS (Depth-First-Search)
- 스택이나 재귀함수를 활용하여 분기별로 탐색하는 방법이다.
- 모든 노드를 방문하고자 하는 경우에 사용된다.
🪄 JavaScript로 구현
// 인접 리스트 그래프
const graph = {
A: ["B", "C"],
B: ["A", "D", "E"],
C: ["A", "F", "G"],
D: ["B", "H", "I"],
E: ["B", "J"],
F: ["C"],
G: ["C", "K"],
H: ["D"],
I: ["D"],
J: ["E"],
K: ["G"],
};
const dfs = (graph, startNode) => {
const visited = []; // queue
let needVisit = []; // stack
needVisit.push(startNode);
while(needVisit.length !== 0){
const node = needVisit.pop(); // stack의 후입선출로 pop() 사용
if(!visited.includes(node)){
visited.push(node);
needVisit = [...needVisit, ...graph[node]];
}
}
return visited;
}BFS (Bradth-First-Search)
- 큐를 활용하여 깊이별로 탐색하는 방법이다.
- 두 노드 사이의 최단경로 찾기, 인접한 노드 찾기 등에 사용된다.
🪄 JavaScript로 구현
// 인접 리스트 그래프
const graph = {
A: ["B", "C"],
B: ["A", "D", "E"],
C: ["A", "F", "G"],
D: ["B", "H", "I"],
E: ["B", "J"],
F: ["C"],
G: ["C", "K"],
H: ["D"],
I: ["D"],
J: ["E"],
K: ["G"],
};
const bfs = (graph, startNode) => {
const visited = []; // queue
let needVisit = []; // queue
needVisit.push(startNode);
while(needVisit.length !== 0){
const node = needVisit.shift(); // queue의 선입선출로 shift() 사용
if(!visited.includes(node)){
visited.push(node);
needVisit = [...needVisit, ...graph[node]];
}
}
return visited;
}💬 적용 가능한 문제
그래프의 모든 정점을 방문하는 문제 → DFS, BFS
경로의 특징을 저장해야 하는 문제 → DFS
최단거리 구해야 하는 문제 → BFS
검색하는 그래프가 큰 문제 → DFS
검색하는 그래프가 작은 문제 → BFS
🪄 타겟 넘버
function solution(numbers, target) {
let answer = 0;
function dfs(index, sum) {
if(index === numbers.length) {
if (sum === target) answer += 1;
return;
}
dfs(index + 1, sum + numbers[index]);
dfs(index + 1, sum - numbers[index]);
}
dfs(0, 0);
return answer;
}🪄 게임 맵 최단거리
function solution(maps) {
const dx = [0, 0, 1, -1];
const dy = [1, -1, 0, 0];
const queue = [[0, 0, 1]];
while (queue.length) {
const cur = queue.shift();
if (cur[0] === maps.length - 1 && cur[1] === maps[0].length - 1) return cur[2];
for(let i = 0; i < 4; i++){
const yy = cur[0] + dy[i];
const xx = cur[1] + dx[i];
if(xx >= 0 && yy >= 0 && xx < maps[0].length && yy < maps.length && maps[yy][xx] === 1 ) {
maps[yy][xx] = 0;
queue.push([yy, xx, cur[2] + 1]);
}
}
}
return -1;
}
