[백준] 18352번 : 특정 거리의 도시 찾기

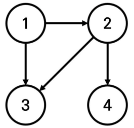
문제

https://www.acmicpc.net/problem/2606

풀이

[백준] 18352 : 특정 거리의 도시 찾기 🥈(실버2)
🎯 29.897%
⏰ 걸린 시간 :55분

• 알고리즘 유형 : [BFS & DFS]

✅ 문제 요약

0. 첫째 줄에 도시의 개수 N, 도로의 개수 M, 거리 정보 K, 출발 도시의 번호 X가 주어진다.
1. M개의 줄에 걸쳐서 두 개의 자연수 A, B가 공백을 기준으로 구분되어 주어진다. 이는 A번 도시에서 B번 도시로 이동하는 단방향 도로가 존재한다는 의미다.

✅ 출력

• X로부터 출발하여 도달할 수 있는 도시 중에서, 최단 거리가 K인 모든 도시의 번호를 한 줄에 하나씩 오름차순으로 출력한다.
• 이 때 도달할 수 있는 도시 중에서, 최단 거리가 K인 도시가 하나도 존재하지 않으면 -1을 출력한다.

⚡️ 주의 사항

0. 시간초과 발생 -> visited를 set()으로 설정하지 않아서 시간초과가 발생했다.
1. recursion DFS로 접근했는데 각 계층을 누적해서 거리를 표현하는게 어려웠다.
2. Layer 문제는 BFS로 풀자

✅ 풀이방법 & BFS 알고리즘로 푼 이유?

✔️ 거리를 이전의 값을 누적해서 더해간다 => Layer 문제
0. distance 계산을 하는 문제지만 두가지 고려해야할 부분이 있다.
1. 누적을 하되 이전에 방문한 적이 있는 노드는 visited에 넣어 관리한다. (이유: 발견은 최소의 거리를 구하기 때문)
2. Que에 (X :start)를 넣어서 빌때까지 BFS를 돌린다.

코드(code)

import sys
from collections import deque
input = sys.stdin.readline
N, M, K, X = map(int, input().split())
# N: N개의 지점, M: M개의 연결, X : start 지점,
graph = [[] for _ in range(N+1)]
Que = deque()
visited = set()

distances = [0]*(N+1)
for i in range(M):
    x, y = map(int, input().split())
    graph[x].append(y)
Que.append(X)
visited.add(X)

while Que:
    node = Que.popleft()
    for next in graph[node]:
        if next not in visited:
            Que.append(next)
            visited.add(next)
            distances[next] = distances[node]+1

if K in distances:
    for destination in range(1,N+1):
        if distances[destination] ==K:
            print(destination)
else:
    print(-1)

회고

BFS 알고리즘 익숙해지도록 해야겠다.
Layer를 나아가며 누적해서 푸는 문제는 BFS알고리즘이 적합하다.
✔️유형 : Layer의 거리를 누적하는 유형

• [해당 코드]

  • visited를 list로 선언했는데 시간초과 발생했다. set() 으로 선언해서 해결함
    https://github.com/JamesJoe0830/ps_study/blob/main/BFS_DFS/2606(%EB%B0%94%EC%9D%B4%EB%9F%AC%EC%8A%A4).py