백준 2597 계단 오르기

📌 문제

백준 2597

유형 : dp

dp인건 알겠는데 점화식을 세우는게 여간 어려운 일이 아닌 듯 하다.

📌 풀이

풀이 1. 2차 배열로 현재까지 연속으로 밟은 계단 저장하기
문제의 조건에서 3번 연속으로 밟으면 안된다는 조건 때문에 현재까지 몇개를 연속으로 밟았는지에 대한 정보가 필요하다.

dp[i][j] : i 번째 계단을 밟았을 때, 현재까지 연속으로 밟은 계단의 개수 j

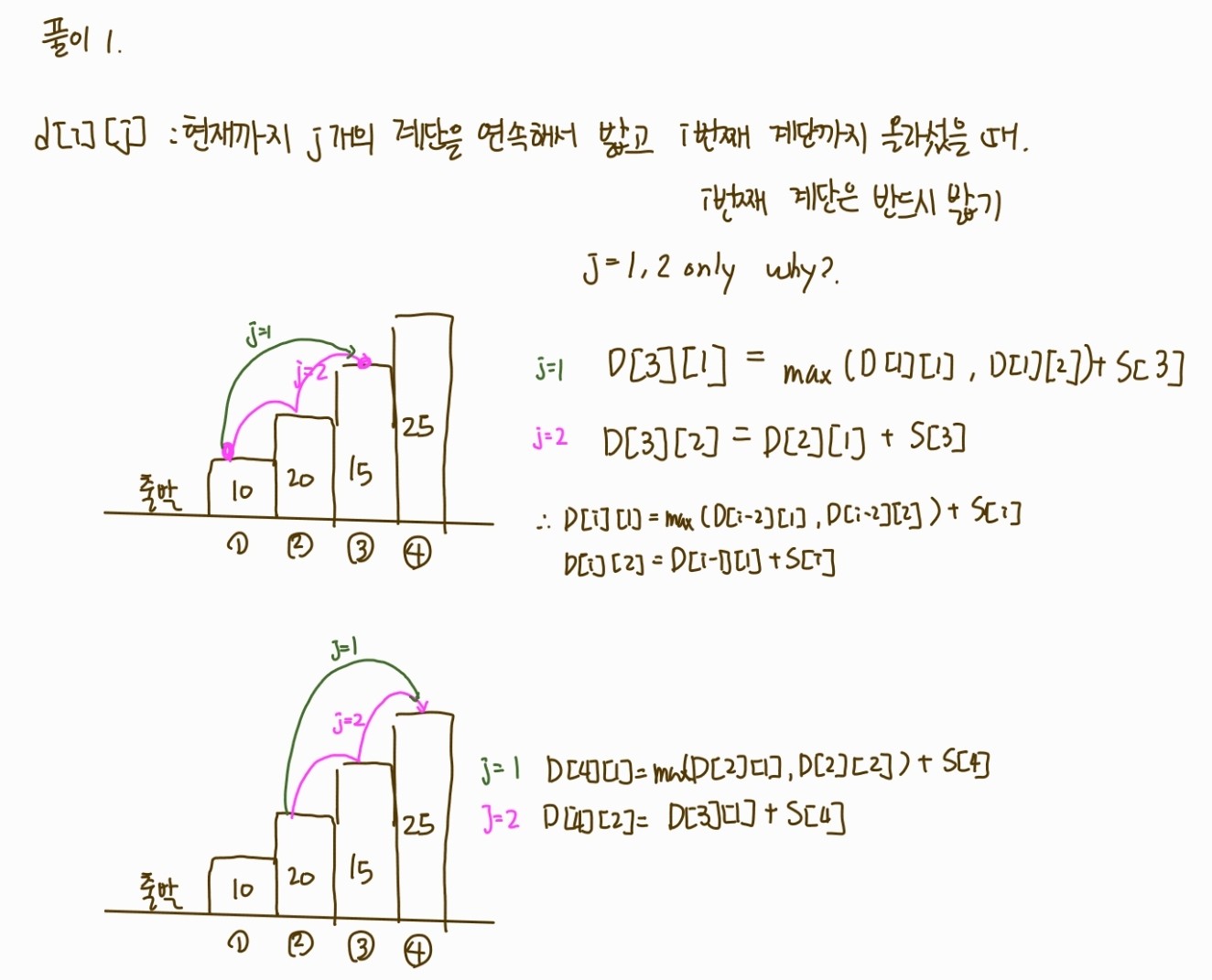
j = 1 일 경우, i - 1 번째 칸은 밟지 않았다. i-2 번째 칸을 밟고 올라오는 경우를 생각하면 되는데, i-2번째 칸에서의 상태는 상관이 없다. 따라서 점화식은

D[i][1] = Math.max(D[i-2][1], D[i-2][2]) + S[i]

j = 2 일 경우, 무조건 i-1 번째 칸을 밟고 올라온다. 따라서 점화식은 i-1 번째 칸을 밟고 오며 이 당시에 j = 1 인 경우만 따진다. (j = 2 이면 세 개 연속으로 밟으면 안된다는 조건 위배)

D[i][2] = D[i-1][1] + S[i]

참고로 위 점화식에서 미지수가 3개가 보이니 최소한 초기값은 3개임을 알 수 있다.

풀이 2. 1차 배열로 밟지 않을 계단의 최소 합 저장하기

D[i] : i 번째 계단까지 올라섰을 때 밟지 않을 계단의 합의 최솟값, 단 i번째 계단은 반드시 밟지 않을 계단으로 선택해야함

우리는 최대한 계단을 밟아줄 예정이고 최소한으로 계단을 넘겨뛸 것이다.

만약 i 번째 계단을 올라왔는데 밟지 않을 예정이라면 i-1 번째 계단은 무조건 밟고 있어야한다. 이때 i-1, i-2, i-3 세개를 연속으로 밟는 경우는 제외시켜야한다. 3개 연속으로 밟지 않기 위한 케이스는 두가지이다.

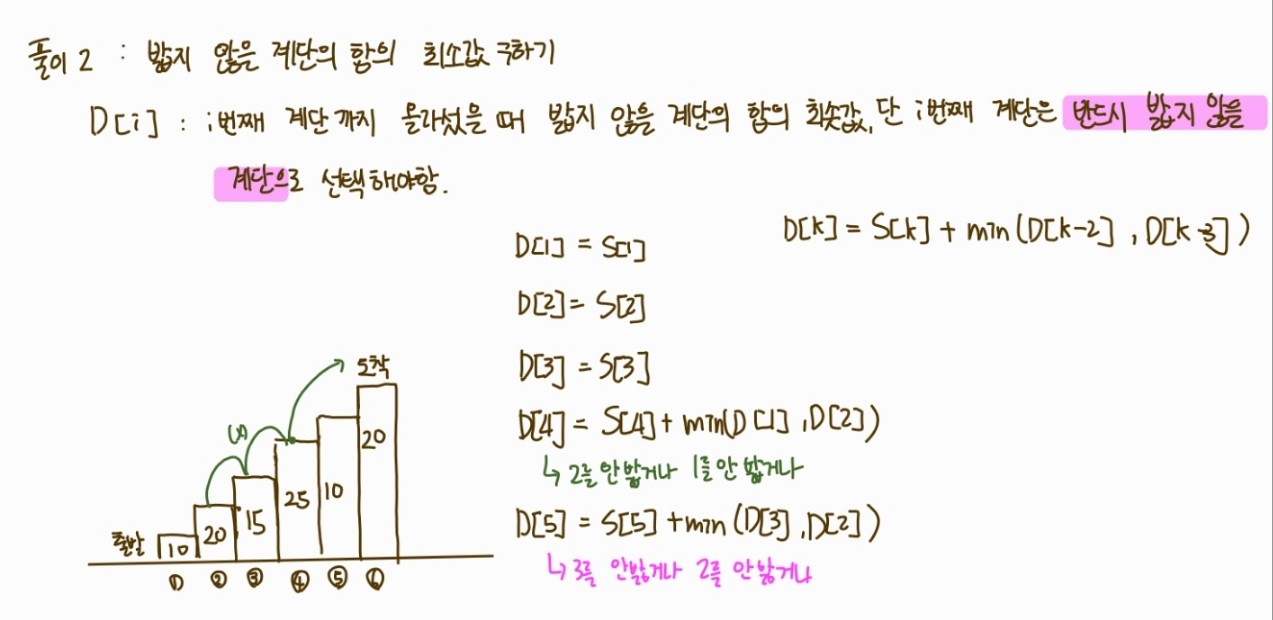
case 1. i-2 번째 계단을 밟지 않는다.
D[i] = S[i] + D[i-2]

case 2. i-3 번째 계단을 밟지 않는다.
D[i] = S[i] + D[i-3]

이중에서 최솟값을 고르면 되므로
D[i] = S[i] + Math.min(D[i-2], D[i-3])

마지막으로 종료 조건에서는 우리가 항상 마지막 계단을 밟아야한다. 따라서, 한칸 넘어서 도착한 경우 (D[n-1]), 두칸 넘어서 도착한 경우 (D[n-2]) 두 가지 경우를 고려해야한다.

따라서, 정답은
(모든 계단 합) - Math.min(D[n-1], D[n-2])

📌 코드

방법 1.

import java.io.*;
import java.util.*;

class Main {
    static public void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int n = Integer.parseInt(st.nextToken());
        int[] s = new int[n+1];

        for(int i = 0; i < n; i++) {
            st = new StringTokenizer(br.readLine());
            int k = Integer.parseInt(st.nextToken());

            s[i+1] = k;
        }

        // dp
        int[][] dp = new int[n+1][3];
        if(n ==1) {
            System.out.println(s[1]);
            return;
        }
        
        dp[1][1] = s[1];
        dp[1][2] = 0;
        dp[2][1] = s[2];
        dp[2][2] = s[1] + s[2];

        for(int i = 3; i <= n; i++) {
            dp[i][1] = Math.max(dp[i-2][1], dp[i-2][2]) + s[i];
            dp[i][2] = dp[i-1][1] + s[i];
        }

        System.out.println(Math.max(dp[n][1], dp[n][2]));
    }

}

방법 2.

import java.io.*;
import java.util.*;

class Main {
    static public void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int n = Integer.parseInt(st.nextToken());
        int[] s = new int[n+1];
        int sum = 0;

        for(int i = 0; i < n; i++) {
            st = new StringTokenizer(br.readLine());
            int k = Integer.parseInt(st.nextToken());
            sum += k;
            s[i+1] = k;
        }

        int[] dp = new int[n+1];
        
        if(n == 1 || n ==2 ) {
            System.out.println(sum );
            return;
        }
        
        dp[1] = s[1];
        dp[2] = s[2];
        dp[3] = s[3];

        for(int i = 4; i <= n; i++) {
            dp[i] = Math.min(dp[i-2], dp[i-3]) + s[i];
        }

        System.out.println(sum - Math.min(dp[n-1], dp[n-2]));
    }

}

ArrayIndexOutOfBound Error가 나올 경우 n = 1 인 경우 array index가 벗어나는 문제가 발생한 것이기 때문에 따로 처리