백준 2293 동전 1

문제 링크

문제 유형

dynamic programming 중에서도 0-1 knapsack problem를 생각하면 된다. 기본적으로 0-1 knapsack problem 를 푸는 방법은 아이템 정렬할 필요 없이 순서대로 아이템을 넣을지 말지를 생각해주면 된다.

dp[0] = 1 이어야 하는 이유는 뒤에 점화식을 보면 알 수 있다.


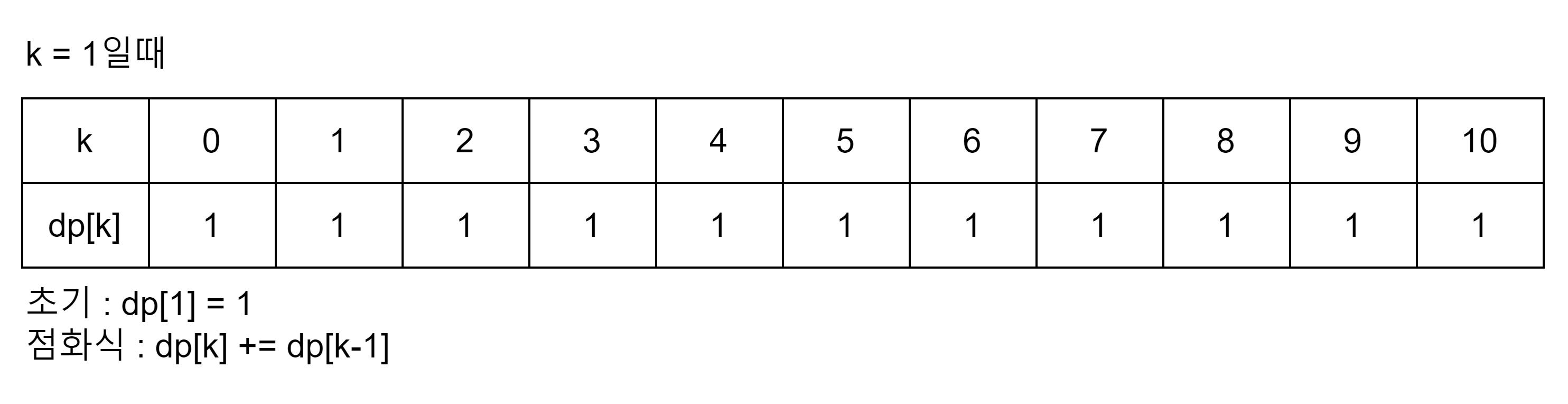
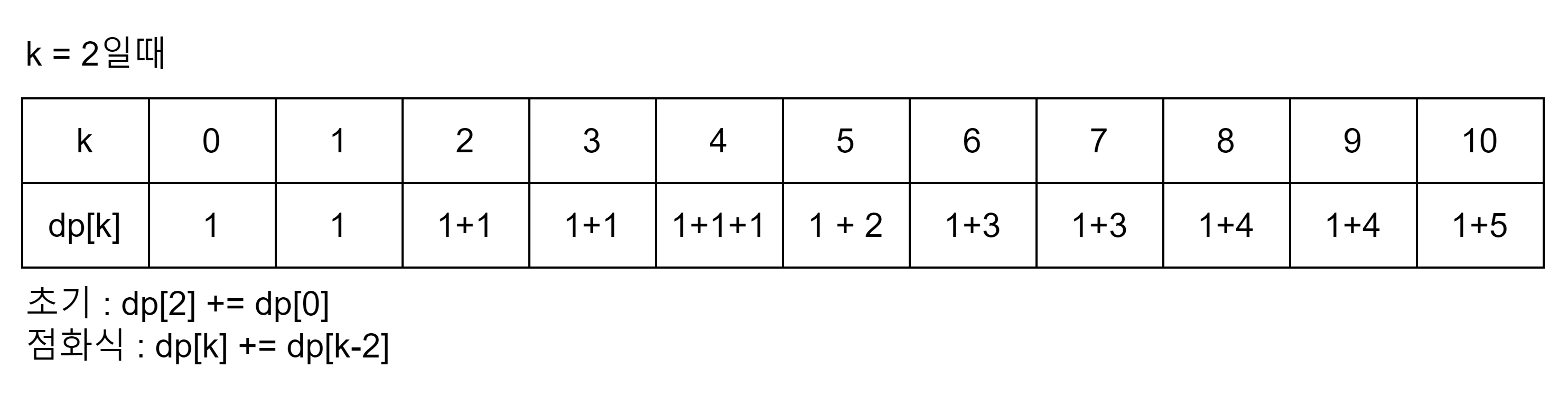
점화식은 dp[k] += dp[k-현재 쓸려는 동전의 가치] 이다.
2원 짜리 동전을 이용할 것이다. (k = 2)
이때 4원의 가치 총합을 만든다고 가정해보자.

4원의 가치를 만들기 위해 2원을 사용하는 경우 dp[4-2] 의 가치를 만드는 경우의 수를 그대로 더해주면 됨을 알 수 있다.

2
= 1 + 1
= 2

4
= 2 + 1 + 1
= 2 + 2

원래 저장되어 있던 dp[4] 가 있을 것이므로 새롭게 만들 수 있는 값만큼 더해준다.

코드

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int n = Integer.parseInt(st.nextToken());
        int k = Integer.parseInt(st.nextToken());
        int[] dp = new int[k+1];
        dp[0] = 1;

        // 0-1 knapsack problem
        for (int i = 0; i < n; i++) {
            st = new StringTokenizer(br.readLine());
            int elem = Integer.parseInt(st.nextToken());
            for(int j = 0; j+elem <= k; j++)
                dp[j+elem] += dp[j];
        }

//        for (int i = 0; i <= k; i++) {
//            System.out.println(dp[i]);
//        }

        System.out.println(dp[k]);
    }
}