[코테, 알고리즘] 프로그래머스 고득점 Kit - 그래프 (3) : 최단경로

📌 그래프는 자료구조편과 알고리즘편, 알고리즘-최단경로편, 코드편 총 4편으로 나누어서 작성

지난번에 못다룬, 그래프 알고리즘 중 최단경로를 탐색하는 알고리즘에 대해 알아보도록 하겠다.

1. 다익스트라 알고리즘 (Dijkstra Algorithm)

(1) 개념

• 특정한 노드에서 출발해서 다른 모든 노드로 가는 각각의 최단경로를 구하는 알고리즘
• 가중치 그래프에서 간선 가중치의 합이 최소가 되는 경로를 찾는 알고리즘
• 그리디 + 동적계획법 : 현재 위치한 노드에서 최선의 경로를 반복적으로 찾으면서 계산해둔 경로를 활용해 중복된 하위 문제를 푸는 형태
• 그래프에 음의 가중치가 존재하지 않아야 한다.

(2) 동작과정

1. 출발노드를 설정하고, 최단거리 테이블을 초기화한다. (출발노드는 0, 나머지는 INF)
2. 방문하지 않은 노드 중 최단거리가 가장 짧은 노드를 선택한다.
3. 해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단거리 테이블을 갱신한다.
   (현재 비용이 현재 테이블의 최단거리보다 짧을때만 값을 교체한다.)
4. 2~3번 과정을 반복한다.

(3) 예시

1. 최단거리 테이블을 시작노드는 0, 나머지는 INF으로 초기화한다.
   heap = [(0,1)]
   
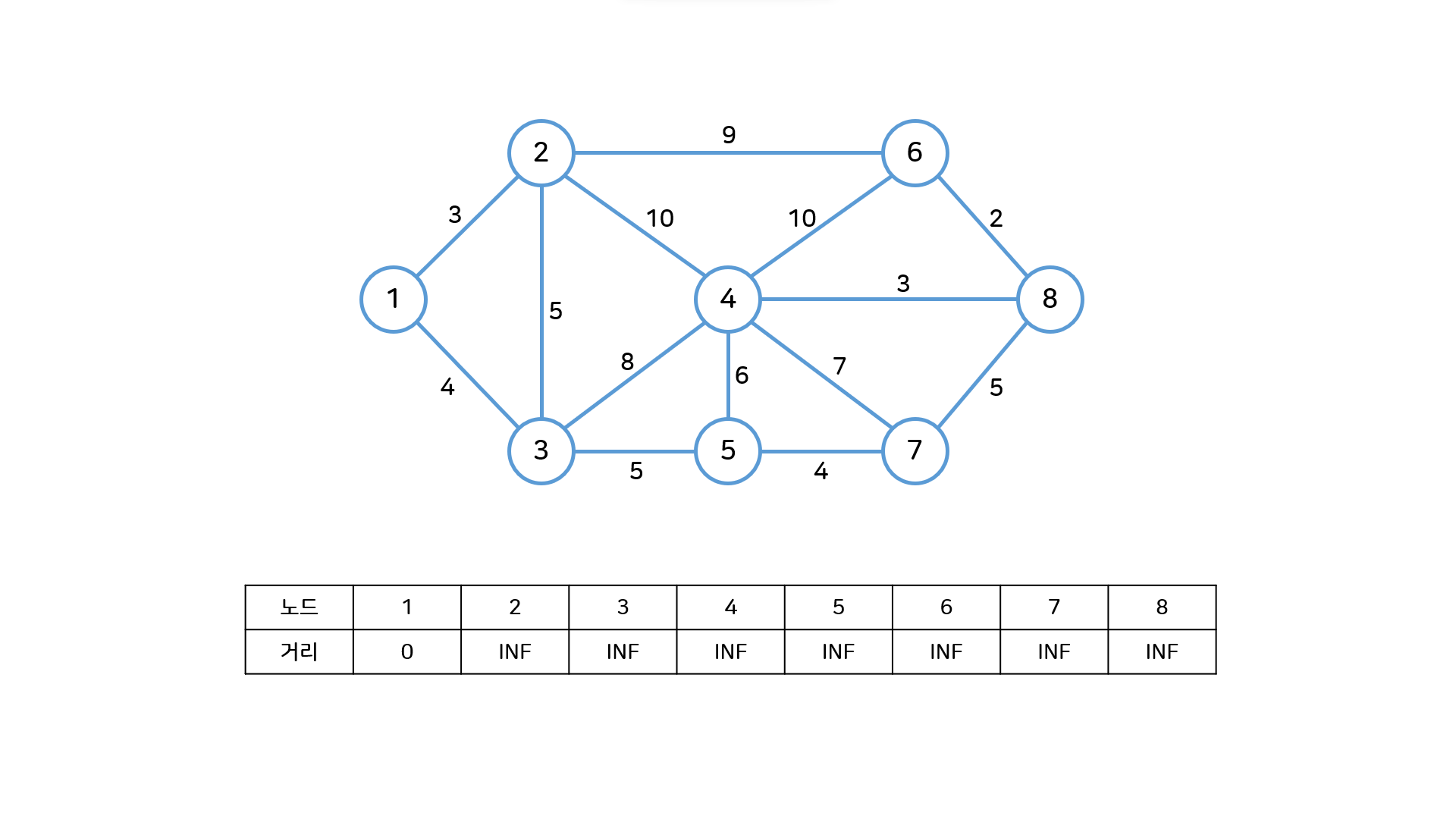
2. 방문하지 않은 노드 중 가장 짧은 최단거리 노드(1번, 시작노드)를 선택하고 해당 노드를 거쳐갈 수 있는 다른 노드(2번, 3번)를 갱신한다.
   heap = [(0,1)] -> pop 1 -> push 2,3 -> heap = [(3,2),(4,3)]
   
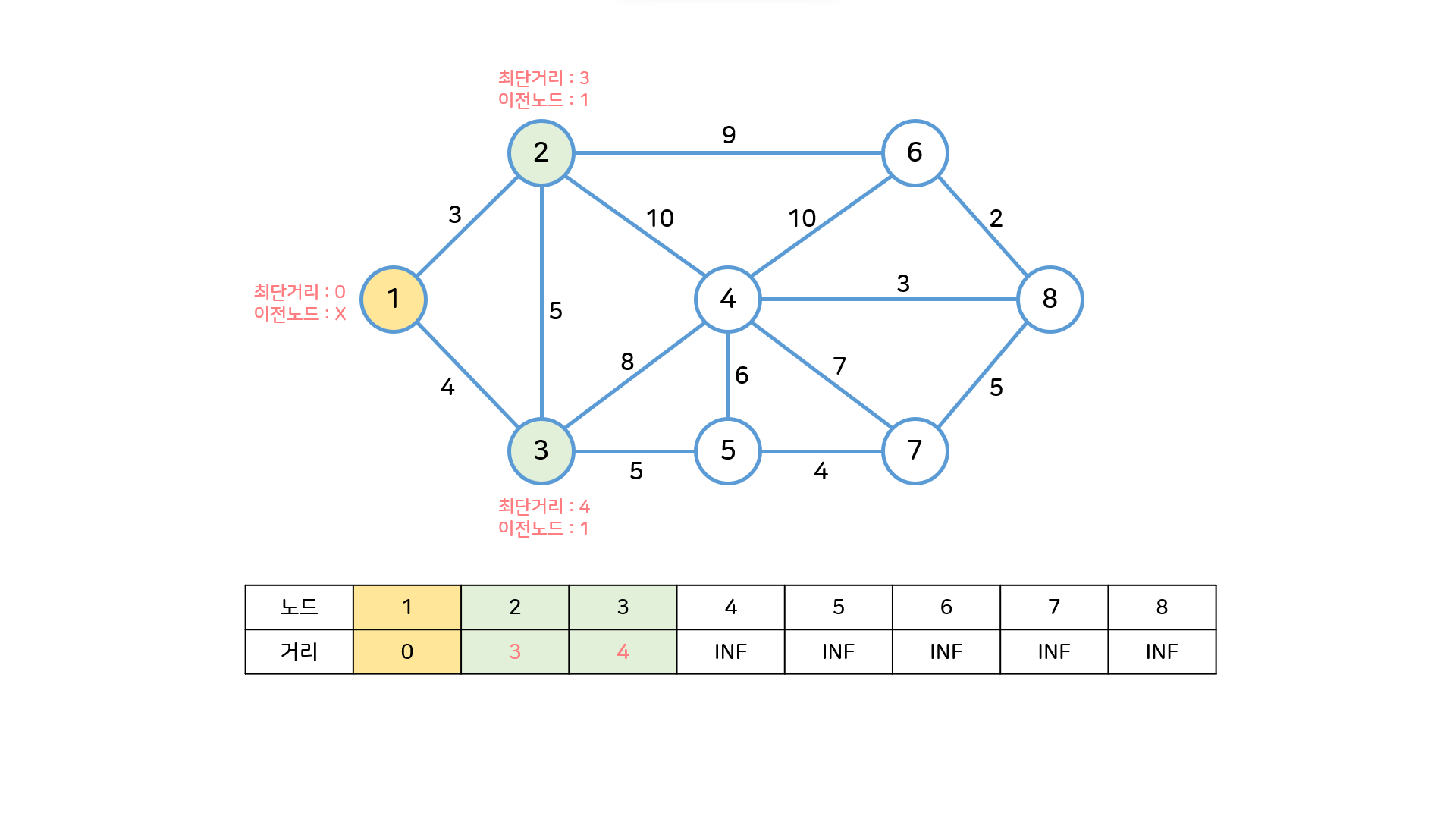
3. 방문하지 않은 노드 중 가장 짧은 최단거리 노드(2번)를 선택하고 해당 노드를 거쳐갈 수 있는 다른 노드(3번, 4번, 6번)를 갱신한다.
   다만 3번은 이전에 갱신해놓은 값이 더 작으므로 무시한다.
   heap = [(3,2),(4,3)] -> pop 2 -> push 4,6 -> heap = [(4,3),(12,6),(13,4)]
   
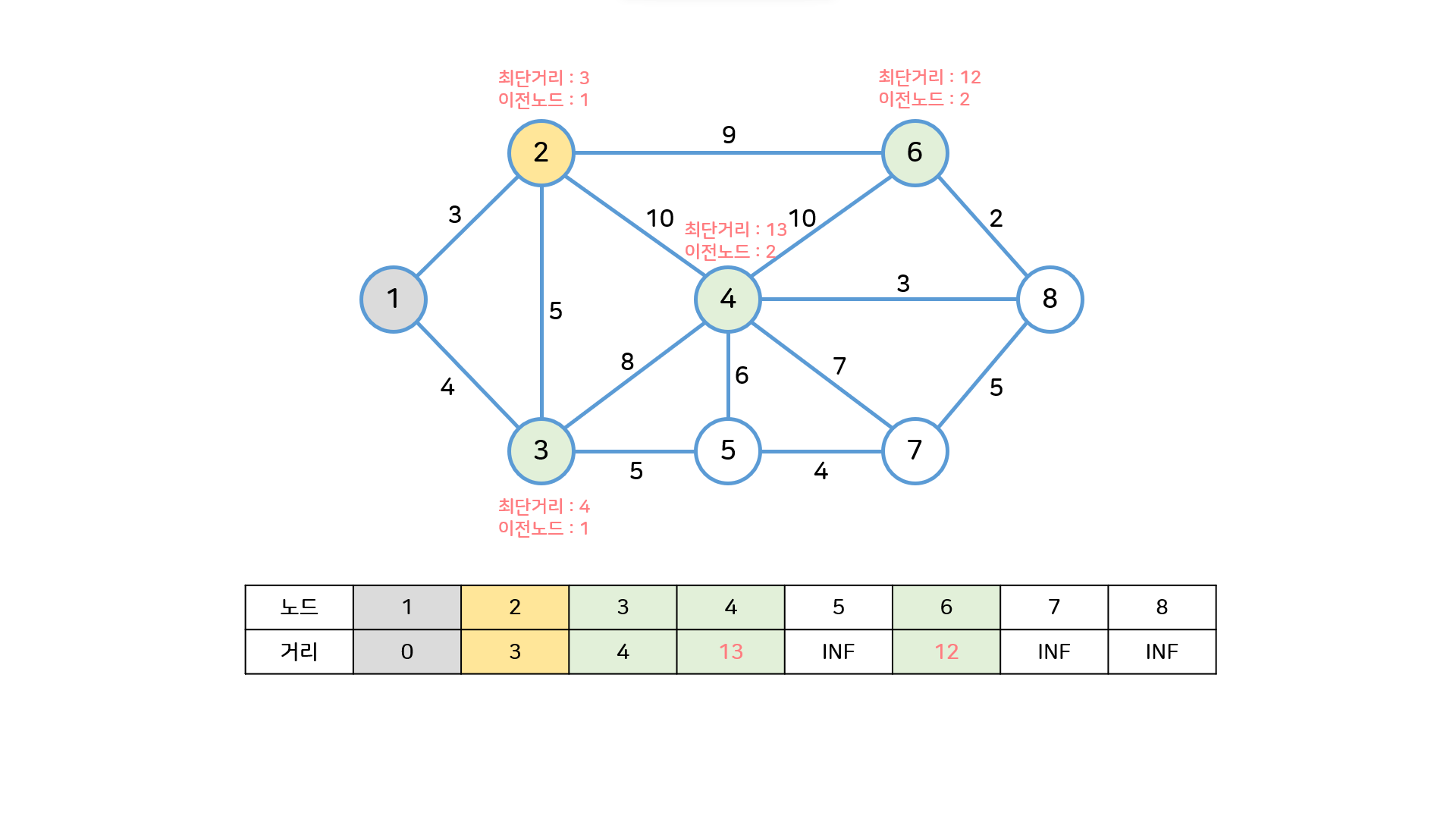
4. 방문하지 않은 노드 중 가장 짧은 최단거리 노드(3번)를 선택하고 해당 노드를 거쳐갈 수 있는 다른 노드(4번, 5번)를 갱신한다.
   여기서 4번은 이전에 갱신해놓은 값보다 더 작아졌으므로 또 갱신한다.
   heap = [(4,3),(12,6),(13,4)] -> pop 3 -> push 4,5 -> heap = [(9,5),(12,6),(12,4),(13,4)]
   
5. 위 과정을 반복하면 아래와 같은 결과가 나온다.
   cf) ❗4번 과정에서 heap에 4번노드가 2개 들어있는데, 이후 과정에서 (12,4)를 먼저 빼서 값들을 갱신한 다음에, 그 이후에 나올 (13,4)는 무시한다.
   

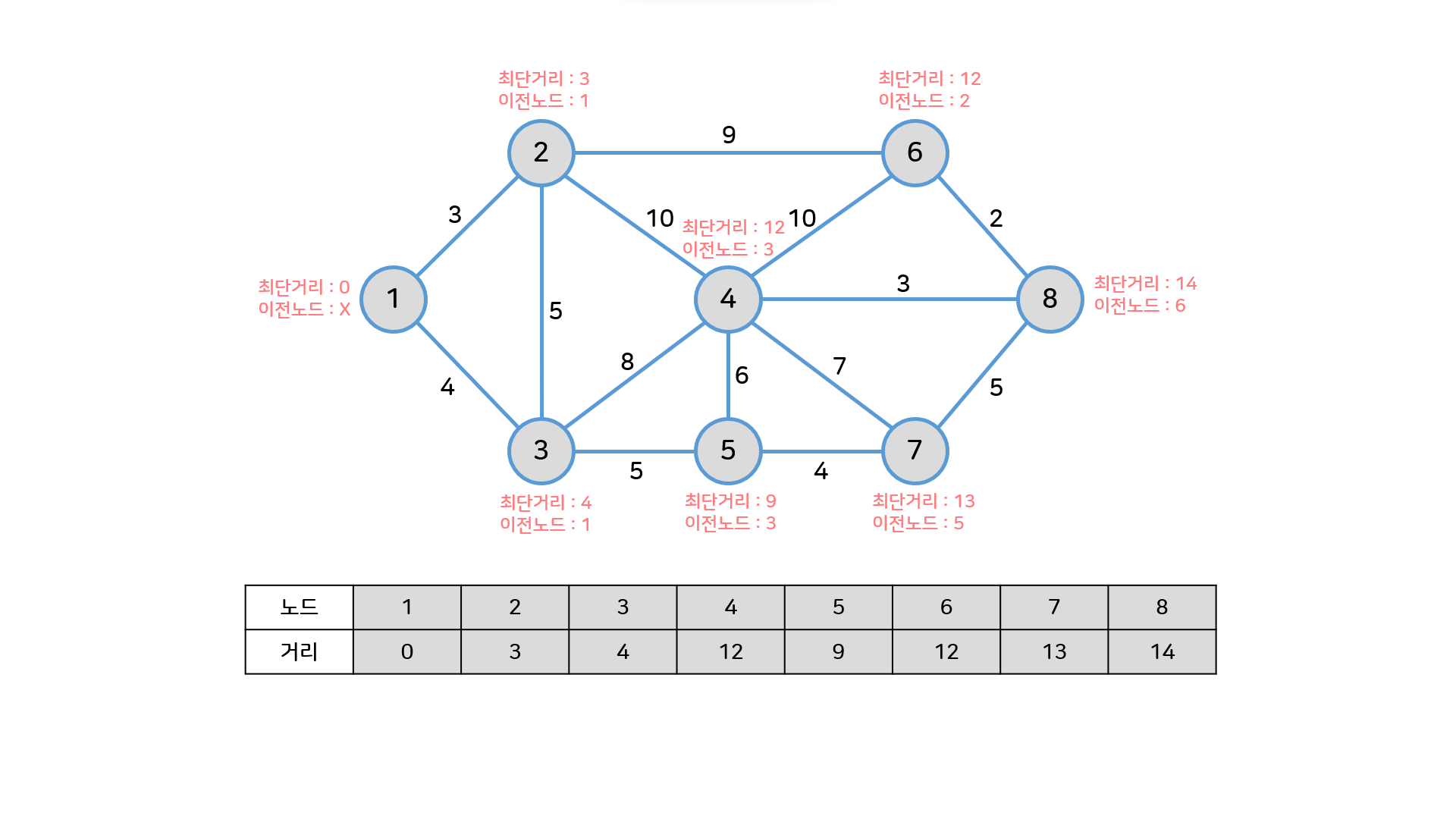
   1번 -> 8번으로 가는 최단거리는 14이고, 8번부터 부모노드를 타고 쭉 타고 올라오면 8<-6<-2<-1라는 경로를 얻을 수 있다.

(4) 구현하기

다익스트라 알고리즘은 힙을 사용해서 구현한다.

import heapq

n = {노드의 개수}
INF = 1e8
distance = [INF] * (n+1) # 최단거리 테이블
graph[출발노드] = [(도착노드, 연결된 간선의 가중치), ...]

def dijkstra(start):
  q = []
  heapq.heappush(q, (0, start)) # (최단거리, 노드번호)
  distance[start] = 0 # 시작노드는 최단거리 0

  while q:
    dist, now = heapq.heappop(q) # 최단거리가 가장 짧은 노드부터 나온다.

    if distance[now] < dist: # 최단거리 테이블에 있는 값이 지금 볼 값보다 작으면 볼 필요 X
      continue

    for node in graph[now]: # 현재 노드에 연결된 모든 노드
      if dist + node[1] < distance[node[0]]: # 기존에 입력되어있는 값보다 작으면
        distance[node[0]] = dist+node[1] # 갱신
        heapq.heappush(q, (dist+node[1], node[0])) # 다음 계산을 위해 큐에 삽입

2. 벨만 포드 알고리즘 (Bellman Ford Algorithm)

➕) 2023-08-20 추가 : 쓸 일 없을 줄 알고 대충 넘어갔다가 백준에 딱 잡혀서 정리하러 다시 돌아옴

(1) 개념

• 음수 간선이 포함되어 있을때 다익스트라 알고리즘 대신 쓸 수 있는 최단경로 알고리즘이다.
• 다익스트라는 방문하지 않은 노드 중에서 최단 거리가 가장 가까운 노드만을 방문하는 반면, 벨만 포드는 매 단계마다 모든 간선을 전부 확인하면서 모든 노드간의 최단 거리를 구해나간다.
• 다익스트라와 동일하게 하나의 시작점에서 다른 모든 노드로 가는 최단경로를 찾는다.
• 음수 사이클이 있는 경우에는 최단거리를 구할 수 없다고 정의하는데(음수 사이클을 무한히 돌면 최단거리는 음의 무한대까지 작아지기 때문에), 벨만 포드 알고리즘으로 음수 사이클의 존재여부를 알 수 있다.
  => 사이클에 존재하는 가중치의 합이 음수일때만 음수 사이클이라고 한다. 사이클에 음수 가중치가 포함되어 있어도 합이 양수이면 음수 사이클이 아니다.
• 시간복잡도는 O(VE)로 다익스트라(O(ElogV))보다는 느리지만 음수 간선이 있어도 최단거리를 찾을 수 있고, 똑같이 음수 간선이 있어도 최단거리를 찾을 수 있는 알고리즘인 플로이드 워셜(O(V^3))보다는 시간복잡도가 짧다.

(2) 동작과정

1. 출발노드를 설정하고 최단거리 테이블을 초기화한다. (출발노드는 0, 나머지는 INF)
2. 모든 간선 E개를 하나씩 확인한다.
   => 간선을 확인하는 순서는 아무 상관이 없다.
3. 각 간선을 거쳐 다른 노드로 가는 비용을 계산하여 최단거리 테이블을 갱신한다.
   => 이때, 간선의 출발 노드가 '한번이라도 계산된 정점', 즉 최단거리 테이블에서 INF가 아닐때만 해당 간선이 잇는 도착 노드까지의 거리를 비교 후 업데이트한다.
   => 다시 말하면 시작노드와 이어져 있는 노드에 대해서만 값을 갱신하는 것이다. 시작노드와 아직 이어져 있지도 않은 노드로부터 비용을 더해 비교하는 건 의미가 없다.
4. 2~3번 과정을 V(정점의 개수) - 1번 반복한다.
5. 음수 사이클이 존재하는지 알고 싶다면, 2~3번 과정을 한번 더 반복했을 때(즉, V번째 반복차례에) 최단거리 테이블이 갱신된다면 음수사이클이 존재하는 것이다.

모든 노드 간의 최단거리를 서서히 완화시켜가면서 실제 최단거리를 구하는 방식이다.

◈ V-1번 반복하는 이유

가장 의문이었던 점은 4번에서 왜 모든 간선을 확인하는 과정을 V-1번 반복해야 하냐는 것이었다. 인터넷을 찾아보면 다 정점 V개를 지닌 그래프에 음수 사이클이 없을때, 최단경로는 한 정점을 2번 지나는 일이 없으며, 최단경로는 간선을 최대 V-1개만을 가지기 때문이라고 한다.

근데 그거랑 이거랑 뭔 상관?? 우선 예시를 보자. (아래 예시는 모두 코드 상에서의 동작예시임)

- 예시1

0. 아래와 같은 그래프가 있고, 시작점 1번 노드부터 가장 먼 4번 노드까지의 최단경로를 찾는다고 가정해보자. 간선 확인 순서는 가장 최악의 상황을 가정하기 위해 C->B->A 순서대로 확인한다고 하자.
   

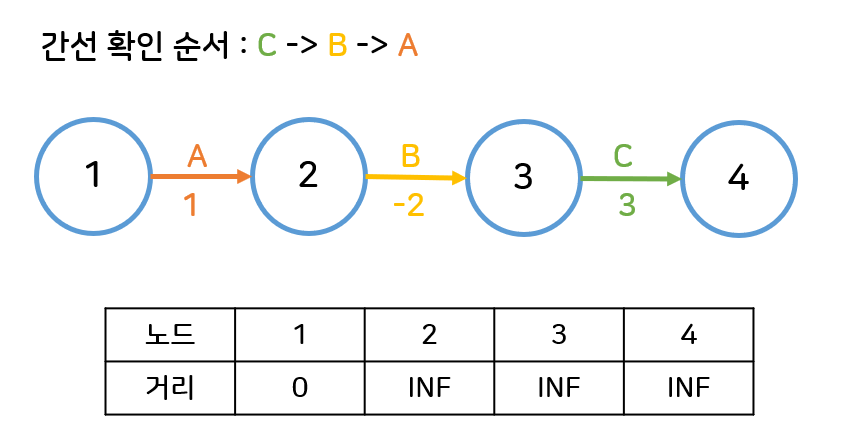
1. 첫번째 반복에서 C와 B는 각 간선의 시작점이 아직 INF이기 때문에 갱신하지 않는다. A 간선에서만 업데이트를 진행한다.
   

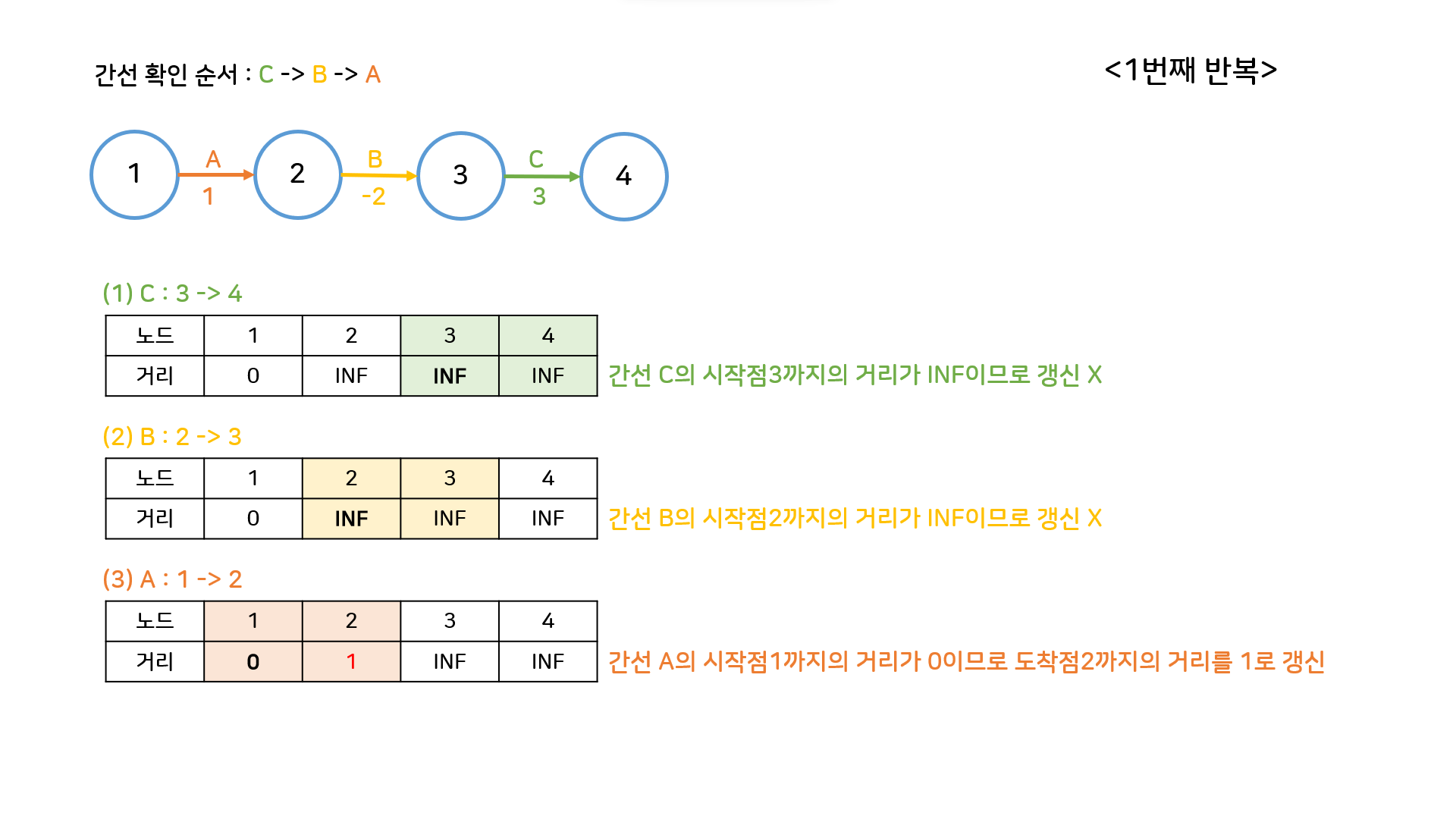
2. 두번째 반복에서는 첫번째 반복에서 노드2까지의 거리가 갱신되었으므로, B를 확인할때 이전에 못했던 갱신을 할 수 있다. C는 아직도 갱신할 수 없는 상태다.
   

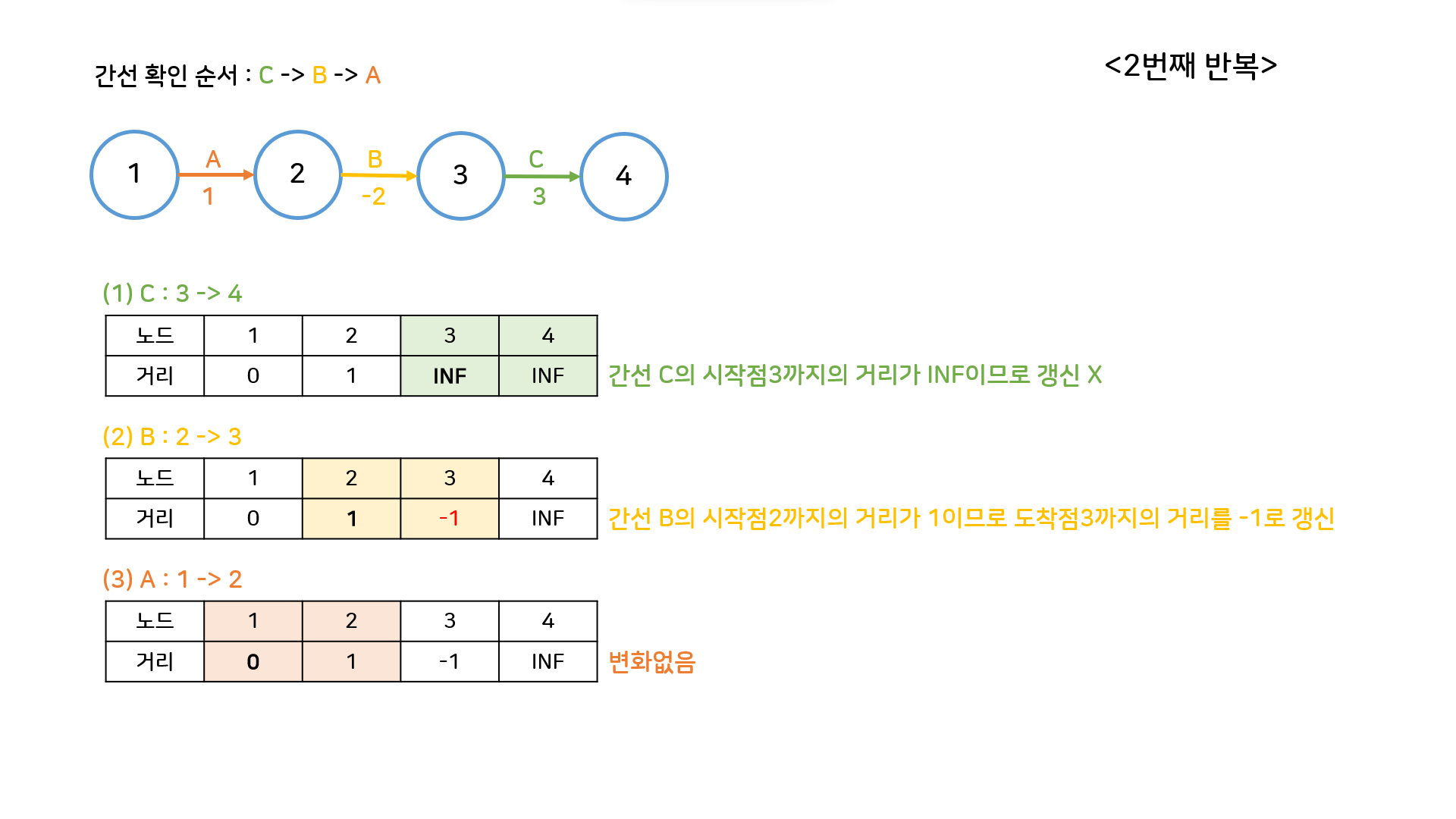
3. 세번째 반복차례가 돼서야 비로소 C를 사용하는 경로를 갱신할 수 있게 된다. 정점의 개수가 4개이므로, 이번 반복이 마지막이다.
   

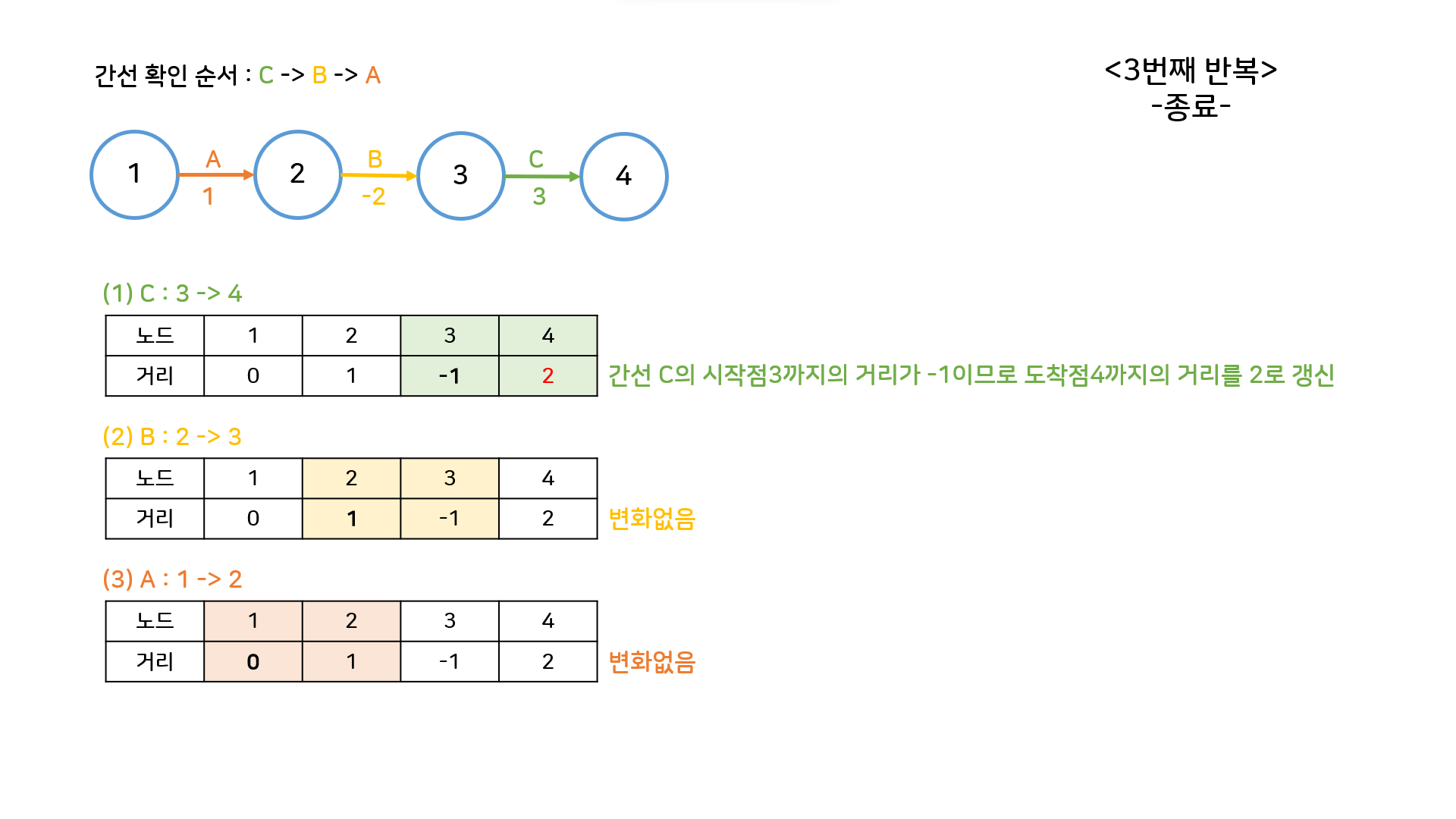
4. 음수 간선 확인을 위해 한번 더 반복문을 돌려보자. 이 예시는 음수사이클이 없으므로, 네번째 반복에서는 최단거리 테이블이 갱신되는 부분이 하나도 없다.
   

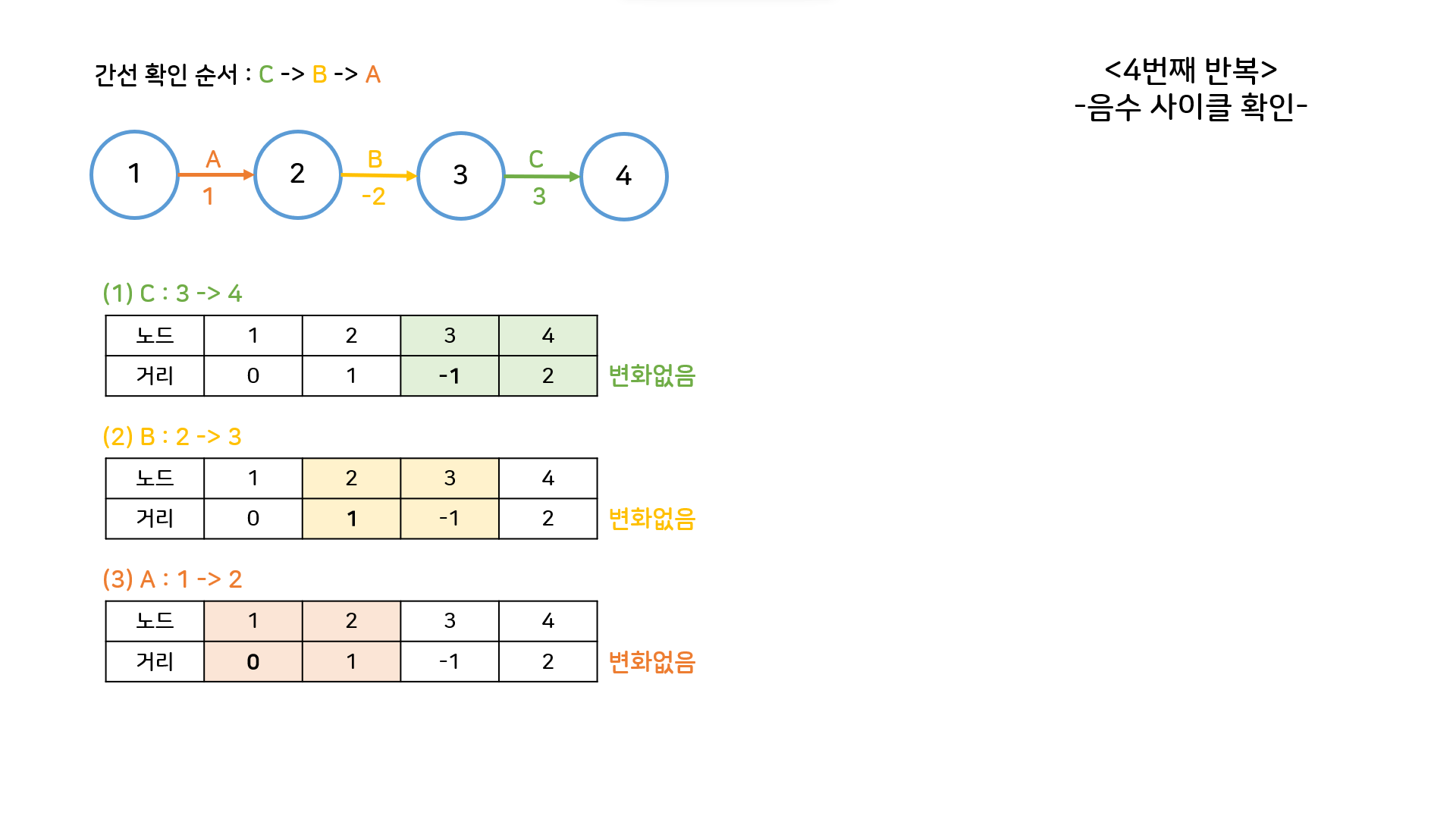
이 경우에는 노드가 4개이기 때문에 최단경로는 최대 3개의 간선을 가질 수 있었고, 이에 따라 반복문을 3번 수행했을 때 실제 최단경로를 구할 수 있었다. 여기서 노드가 V개일때 최단경로를 구하려면 간선 확인을 최소 V-1번 반복해야한다는 것을 유추해낼 수 있다.

- 예시2 (혼돈의 시작)

그런데 만약에 운이 좋아서 간선 확인을 A->B->C 순으로 했으면 어떻게 될까?

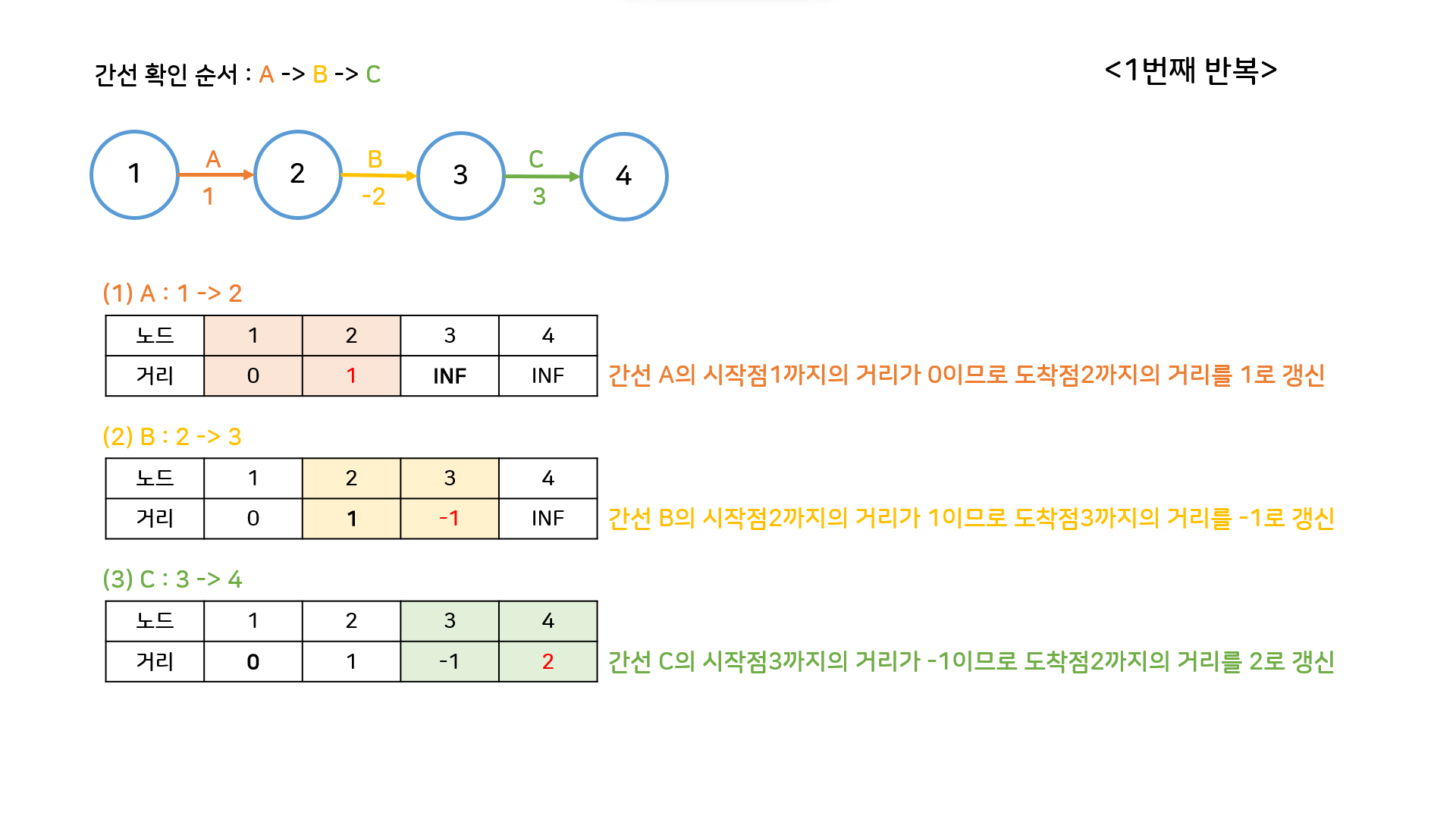
첫번째 반복에서 이미 답이 구해져버리고, 두번째부터 V-1번째까지 아무런 의미 없는 반복문이 이어진다. 이럴 경우 이후 반복문은 실행하지 않아도 된다.

그럼 아까 말한 V-1번 반복은 어디다 팔아먹은걸까?? 조금 이따 알아보도록 하자.

- 예시3

또다른 가정으로, 만약에 음수 사이클이 있었다면 어땠을까?

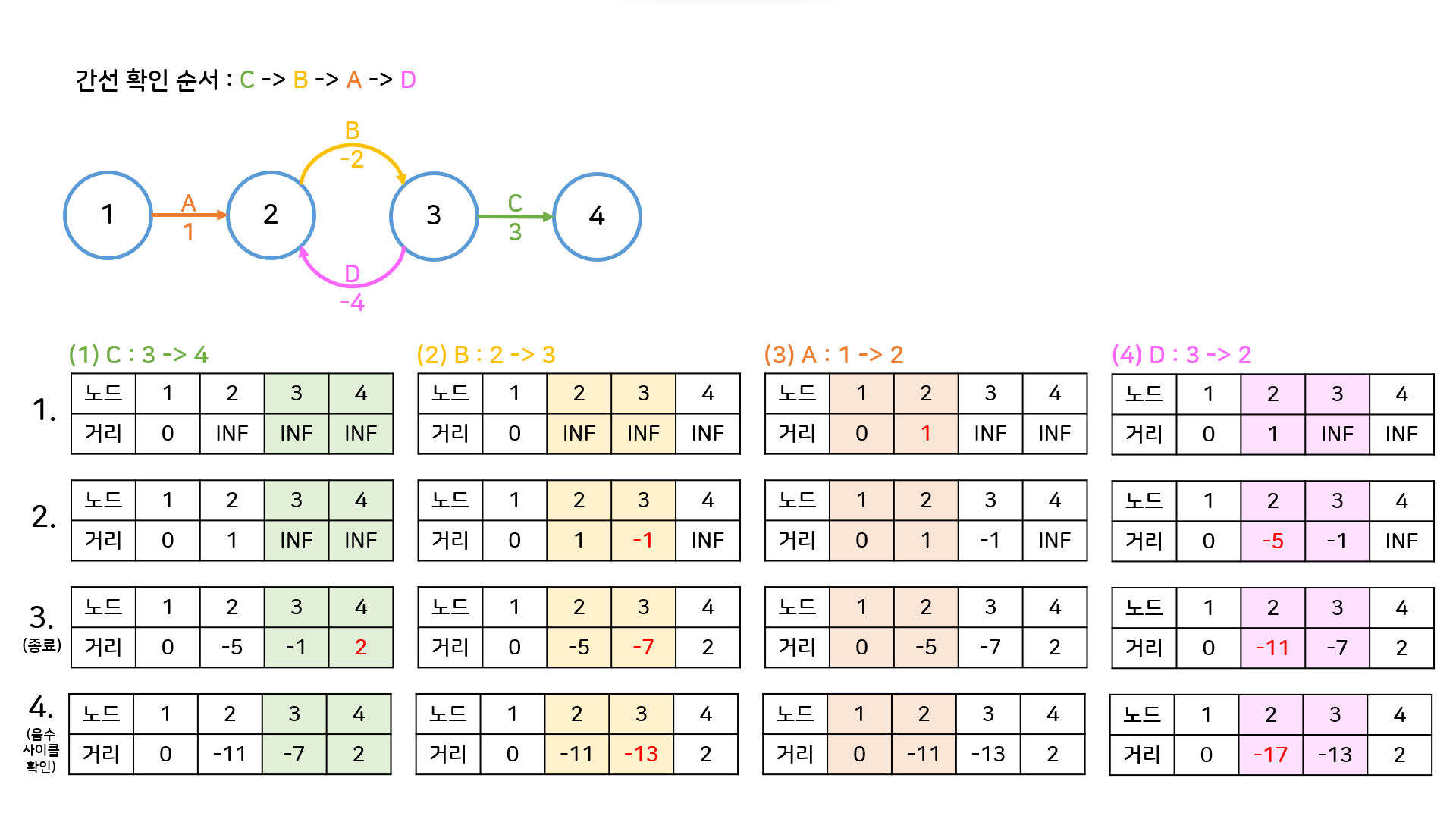
음수 사이클이 있을때는 4번째 반복차례에도 최단거리 테이블이 갱신되고 있는 것을 볼 수 있다. 이 부분에 착안해서 음수사이클의 존재를 찾아내는 것이다.

◈ 그래서 ...

알고리즘 설명과 코드가 일치하지 않는 부분이 있어서 거기서 엄청나게 혼동이 온 것 같다.

혼란하다 혼란해!

더 찾아보니 k번째 루프는 시작점으로부터 k개의 간선을 거쳐 도달할 수 있는 최단경로를 모두 갱신해주는 것이라고 하는데, 이를 중점으로 다시 생각해보겠다.

아까 다시 보기로 했던 예시2같은 경우에, (그림 그리기 귀찮ㅜ)

코드 ver.

• 운이 좋아서 루프 한번만에 모든 갱신이 끝나버림

알고리즘 설명 ver.

• 1번째 루프 : 시작점(1)으로부터 1개의 간선을 거쳐 도달할 수 있는 최단경로
  => 간선A(1->2)를 통해 노드2까지의 최단경로를 구할 수 있다.
• 2번째 루프 : 시작점(1)으로부터 2개의 간선을 거쳐 도달할 수 있는 최단경로
  => 간선A(1->2), 간선B(2->3)를 통해 노드3까지의 최단경로를 구할 수 있다.
• 3번째 루프 : 시작점(1)으로부터 3개의 간선을 거쳐 도달할 수 있는 최단경로
  => 간선A(1->2), 간선B(2->3), 간선C(3->4)를 통해 노드4까지의 최단경로를 구할 수 있다.

그래서 알고리즘상으론 최단경로는 최대 V-1개의 간선을 가지기 때문에 V-1번의 루프를 돌려야하는데, 코드에서는 간선 방문 순서에 따라 더 빨리 끝날 수도 있는거다. 운이 나빠서 최악의 경우였어도 최대 V-1번만 반복하면 무조건 최단거리가 나온다는 것이 보장되기 때문에 코드에서도 V-1번 돌리는 거다.

(틀렸을수는 있음..)

(3) 구현하기

INF = int(1e9)
V, E = map(int, input().split())
edges = []
distance = [INF] * (V + 1)

for _ in range(E):
    s, d, w = map(int, input().split())
    edges.append((s, d, w)) # edges = [(시작점, 도착점, 비용),...]
    
def bellman-ford(start):
	# 시작점은 0, 나머지는 INF
    distance[start] = 0
    # 최단거리 갱신 V-1번 + 음수사이클 판별용 1번 = 총 V번 반복
    for i in range(V):
    	# 모든 간선들 확인 (순서 무관)
        for s, d, w in edges:
        	# 이미 방문한 시작점 & 도착점까지의 거리보다 시작점까지의 거리 + 비용이 더 작을때
            if distance[s] != INF and distance[d] > distance[s] + w:
            	# 최단거리 갱신
            	distance[d] = distance[s] + w
                # 최단거리 갱신했는데 사실 이게 V-1번째 반복이었다면?
                if i == V - 1:
                	# 음수 사이클 발생
                    return True
    return False 
 
negative_cycle = bellman-ford(1)

if negative_cycle:
    print("음수 사이클 발생")
else:
    for i in range(2, V+1):
        if distance[i] == INF:
            print("도달할 수 없음")
        else:
            print(distance[i])

3. 플로이드 워셜 알고리즘 (Floyd Warshall Algorithm)

(1) 개념

• 다익스트라는 하나의 정점에서 다른 모든 정점까지의 최단거리를 구하지만, 플로이드 워셜 알고리즘은 한번의 실행으로 모든 노드 쌍 사이의 최단경로를 구할 수 있다.
• 음의 간선이 있어도 사용할 수 있다.
• 플로이드 워셜은 모든 지점에서 다른 모든 지점까지의 최단거리를 저장해야하기 때문에, 최단거리 테이블을 2차원 테이블로 구성한다.

(2) 동작과정

플로이드 워셜 알고리즘의 점화식

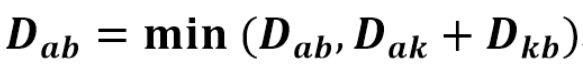
1. 최단거리 테이블을 모두 INF로 초기화한다.
2. 출발노드와 도착노드가 같은 경우는 최단거리 테이블을 0으로 한다.
3. 그래프에서 주어지는 모든 간선에 대해 최단거리테이블[from][to] = weight 형태로 저장한다.
4. 모든 정점을 중간점으로 둔 경우에 대해, 위 점화식을 사용해 값을 계산해서 더 작은 값으로 갱신한다.

(3) 예시

1. 그래프의 노드와 간선에 따라 최단거리 테이블을 초기화한다. (두 노드를 연결하는 간선이 있으면 방향에 따라 그 간선의 가중치를 넣고, 없으면 INF를 넣는다.)
   
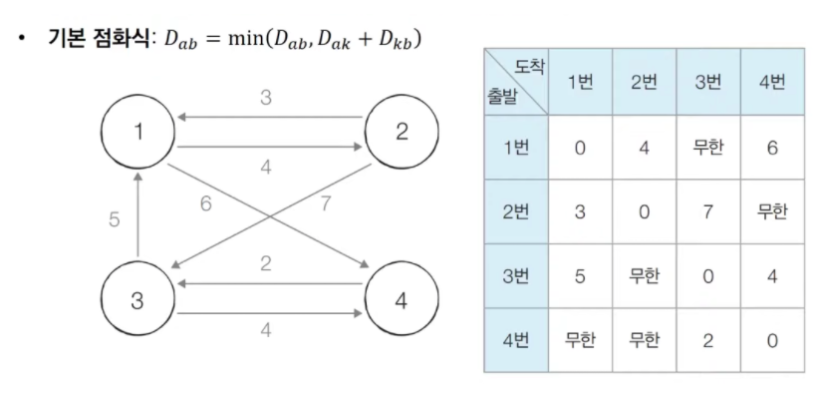
2. 1번 노드를 거쳐가는 경우를 고려해서 테이블을 갱신한다.
   
3. 2번 노드를 거쳐가는 경우를 고려해서 테이블을 갱신한다.
   
4. 위의 과정을 반복하면 아래와 같은 최단거리 테이블이 만들어진다.
   

   1번 -> 3번으로 가는 최단거리는 8이다.

(4) 구현하기

# n = 노드의 개수
def Floyd_Warshall():
	distance = [[INF] * n for _ in range(n)]
	# ~ 최단경로 테이블 초기화 과정은 생략 ~
	for k in range(n):
      for a in range(n):
          for b in range(n):
              distance[a][b] = min(distance[a][b], distance[a][k] + distance[k][b])