학습 주제
깊이/너비 우선 탐색 (DFS/BFS)을 이용한 여행경로 풀기
학습 내용
그래프에 기반한 문제


깊이 우선 탐색 (DFS; Depth-First Search)
- 무향 그래프가 예제로 주어짐
- 0번 노드에서 진행할 수 있는 방향은 1과 2가 있음. 1로 진행했다고 가정.
- 깊이 우선 탐색이다보니, 1에서 끝까지 진행을 마치고 그다음 2로 진행했을 때를 알아보기로 함.
- 방문 한 곳은 재방문하지 않음. 숫자가 낮은 순으로 방문
- 0 -> 1 -> 3 -> 7 -> 4 -> 5 -> 2 -> 6
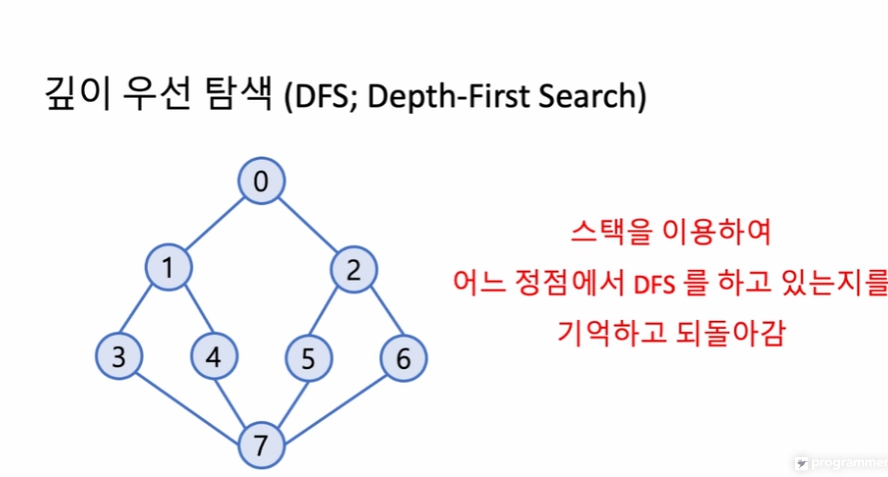
스택을 이용해서, 얼마만큼 진행 했다가, 다시 되돌아 갈 수 있어야함 7 -> 4 -> 5 처럼.
4에 도달 후 더 이상 진행 할 수 없게되면, 다음 순번인 5로 진행 시도할 수 있어야 함.
너비 우선 탐색 (BFS; Breadth-First Search)
- 0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7
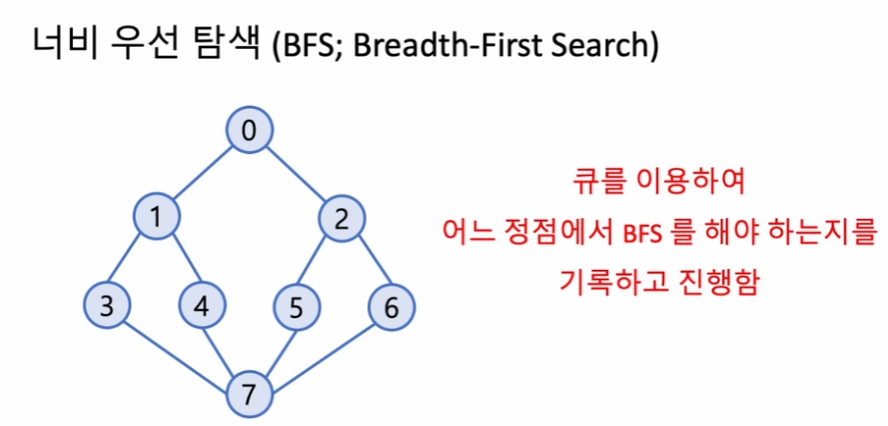
큐를 방문 시, 내가 방문할 노드들을 큐에 집어넣음.
큐 특성상 FIFO 이므로, 3,4는 이전에 넣었던 2 다음에 순회함
문제
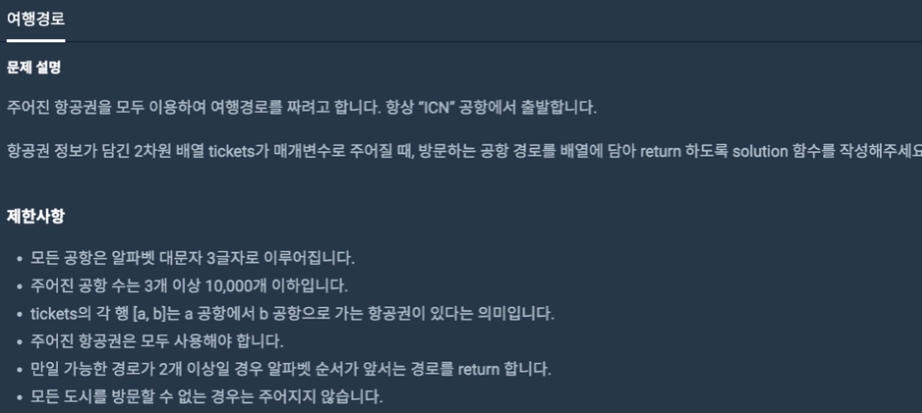
제한 사항
- ticket의 각 행 [a,b]는 a공항에서 b 공항으로 가는 항공권이 있다는 의미
- 주어진 항공권은 모두 사용해야함.
- 가능 경로 2개 이상일 시, 알파벳 앞서는 경로를 먼저 방문
- 소진할 수 없는 경우는 주어지지 않음.
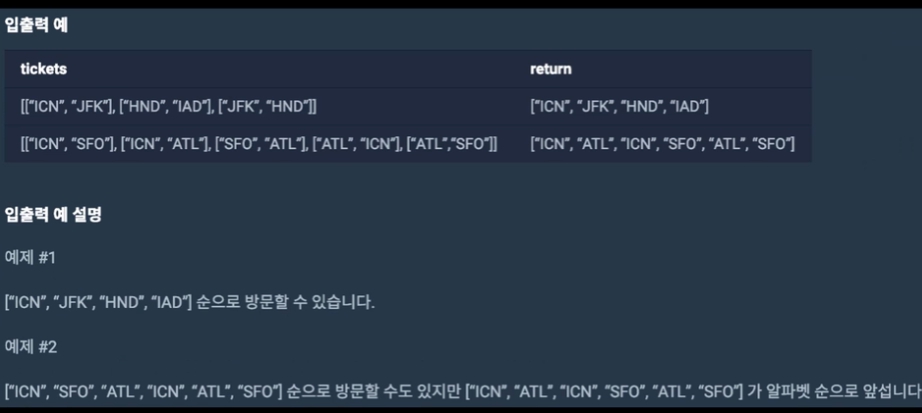
넓이 우선 탐색은 항공권 특성상 할 수 없음. (돌아오는 경우가 없을 수도 있기에)
예제 풀이
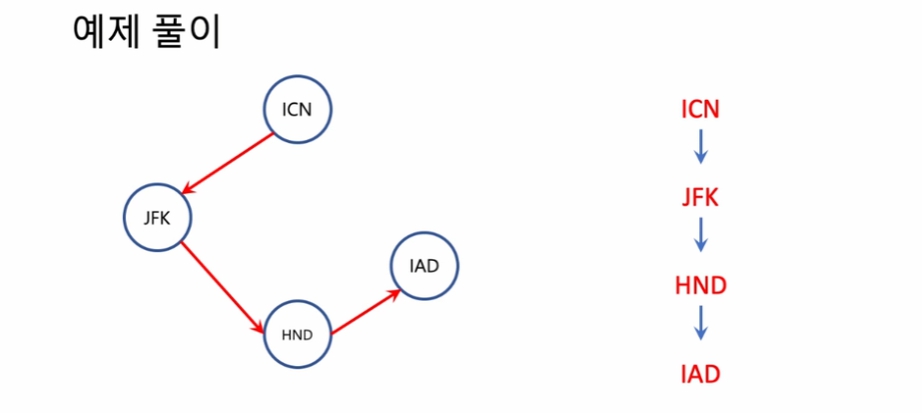
선택지가 없어. 간편하다.
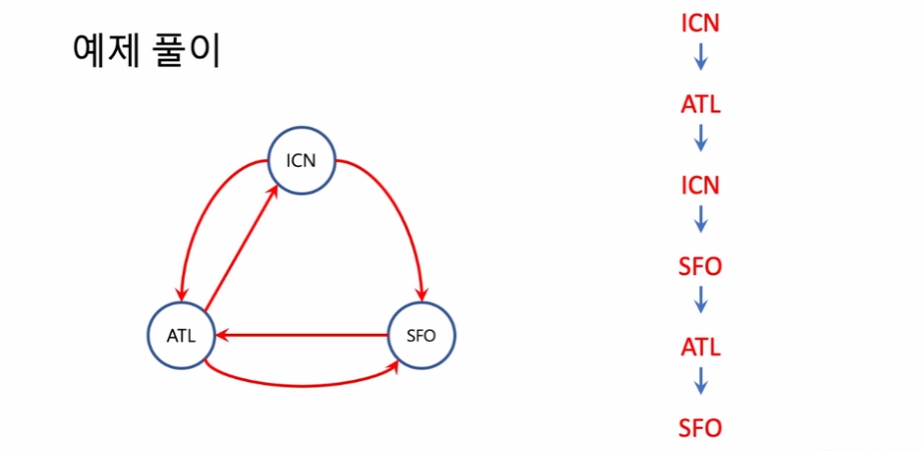
여러 경로가 가능할 때 알파벳이 앞선 경로가 우선하므로, 그 규칙을 따라 진행하면 다음과 같이 모든 경로를 소진할 수 있다.
일종의 한붓그리기를 생각하면 된다.
- 다른 경로
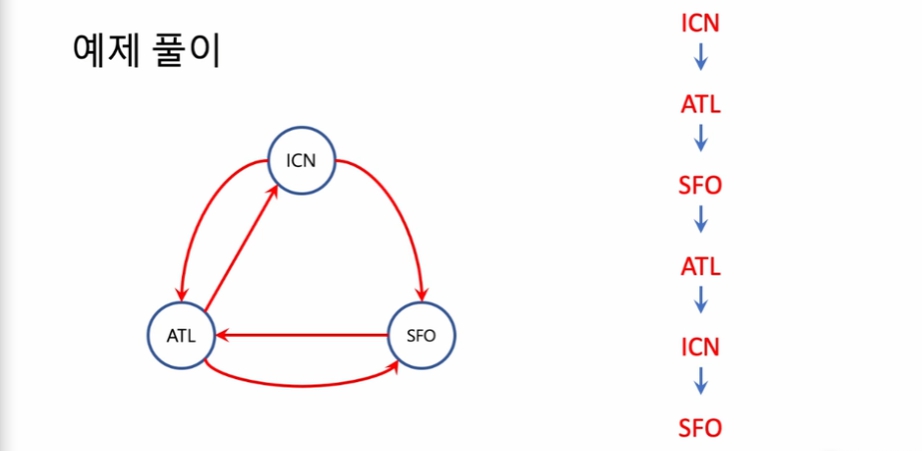
이것도 유효한 한붓그리기.
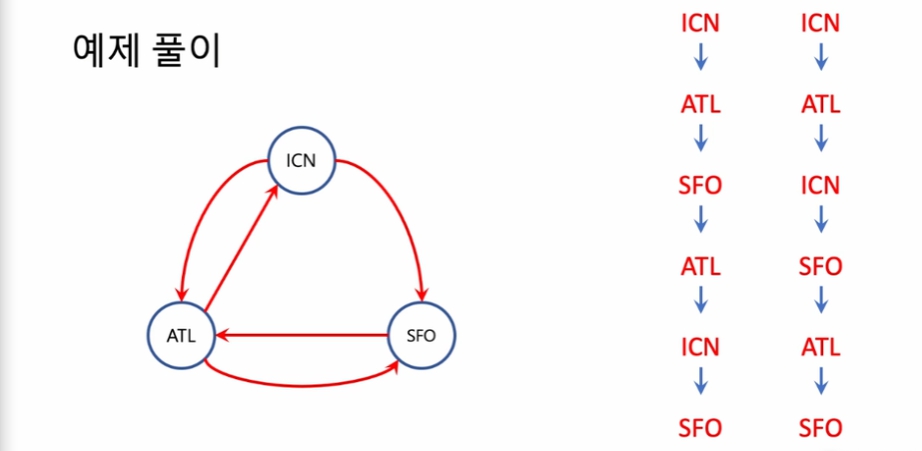
I > S로 앞서기 때문에 이번엔 오른쪽 방식이 답이될 수 있다.
문제의 해결 - 깊이 우선 탐색 (DFS)을 응용
- 한 붓 그리기
- 시작 정점은 언제나 'ICN'
- 모든 정점 방문이 아닌, 모든 간선을 거쳐야
- 순서를 정해야 함.

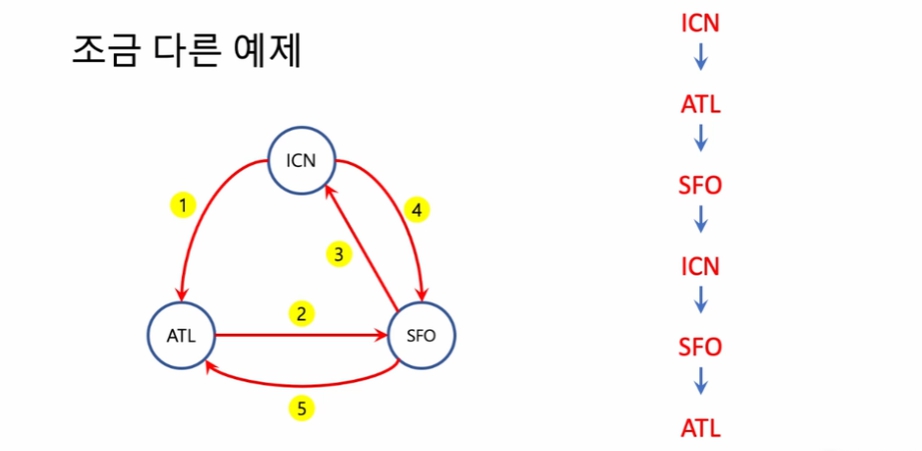
2번 까지 도착 한 뒤 SFO에서 ATL, ICN 선택 가능 알파벳 순서에 따라 ATL먼저 탐색, 그러나 ATL 에서 더 이상 갈 수 있는 선택지가 없음. SFO로 되돌아와서 그 다음 선택지였던 ICN 탐색, 4, 5 번 순으로 진행하여 모든 간선 사용 완료.
- 가다가 선택지가 막힌 경우, 그 전 노드로 되돌아 옴. 여기서 그 다음 선택지로 이동. 안되면 또 그 전 전 노드로 돌아가 탐색.
알고치즘의 설계
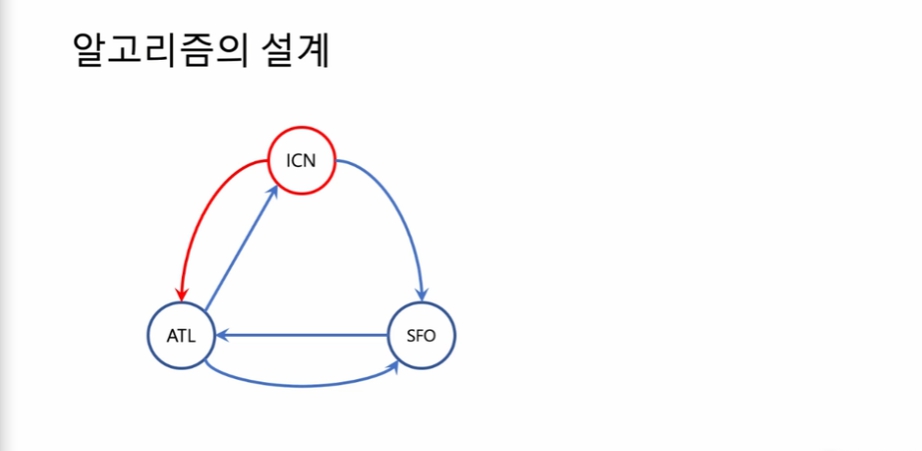
ICN -> ATL 항공권으 썼다고 가정하고 ATL에서 한붓 그리기를 구하는 것과 동일하게 볼 수 있음.
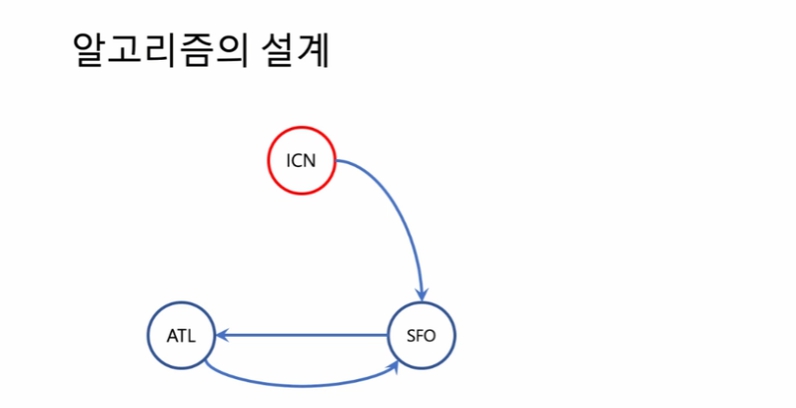
알파벳 순서에 따라 다시 ICN 에 오게되면 항공권은 소모하였다고 가정함.

문제가 재귀적인 성질을 지니고 있음.
알고리즘의 동작
빈 스택을 생성하고, 방문하는 공항을 스택에 저장. 이유는 내가 어디까지 방문 했던 순서가 스택에 저장되어야 함. 중간에 막힐 경우 돌아와서 다음 우선 선택지로 이동해야 함.
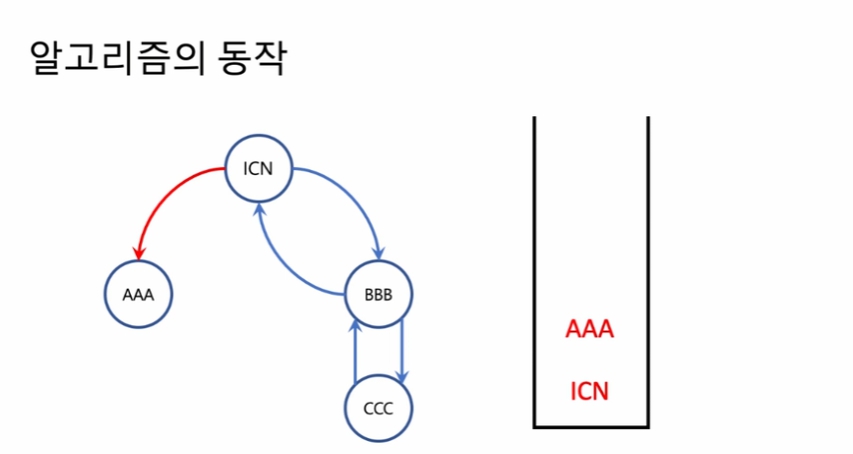
이렇게 AAA에 도착한 뒤 더 이상 진행할 수 있는 간선이 없는 상황에서 아직 사용하지 못한 간선들이 남아 있을 경우 이 선택지는 옳지 못한 선택지이다. 그럼 이 선택을 제외하고 그 다음 우선 순위의 선택지를 순회하여야 한다.
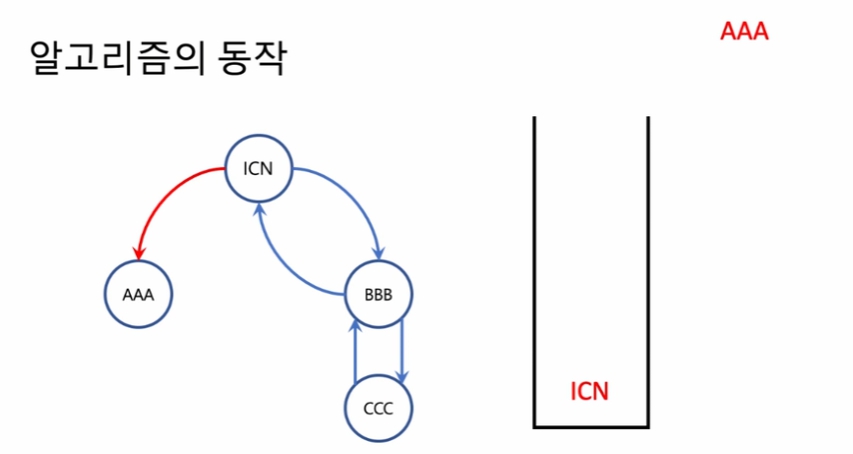
'AAA'를 스택에서 꺼내서 어딘가에 적어둔다. 어디에 적어둘지는 추후 기술
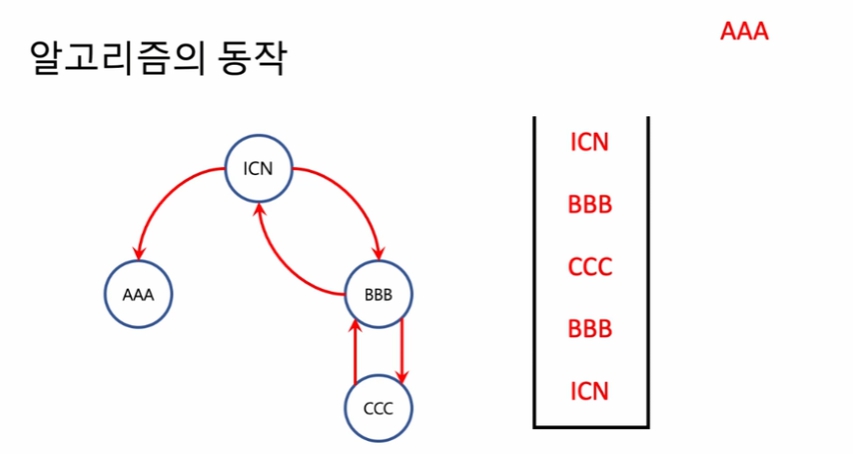
다시 스택을 보면 ICN에서 선택할 수 있는 선택지는 'BBB'가 있다. BBB를 선택한다.
'BBB'에서 갈 수 있는 선택지는 'CCC'와 'ICN' 이 있다. 알파벳 순서에 의해 'CCC'를 선택.
'CCC'에선 'BBB' 선택지가 있어 이동하면, 'BBB'에선 'ICN'선택이가 있다.
최종적으로 'ICN'선택지로 이동하면 모든 간선을 사용하게 된다.
- 이번 문제에선 한붓그리기에 실패할 수 있는 경우는 주어지지 않음.
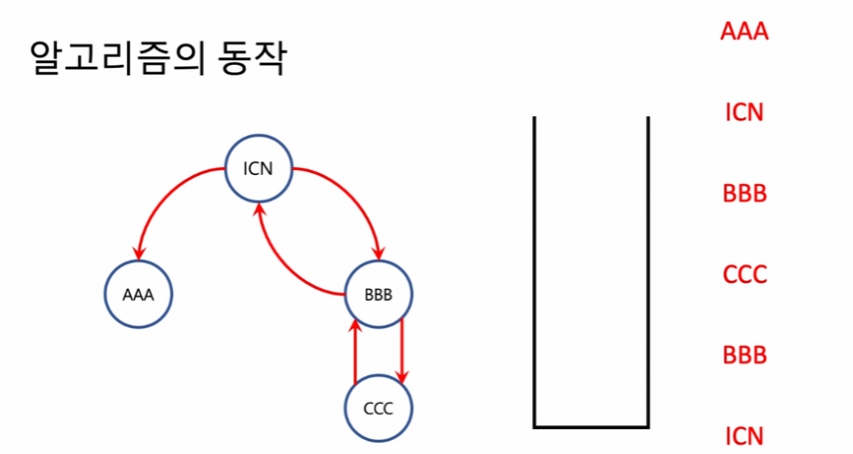
스택에서 순서대로 제거하게 되면 (그전에 가지못했던 'AAA'경로를 제일 마지막으로 함.
그럼 'ICN'에서 갈수 있는 경로가 된다.
요약
- 스택은 본질적으로 재귀적인 성질을 갖고 있음.

어려운 점
이번 문제는 깊이 우선 탐색을 사용해보기 위한 쉬운 예제라는 생각이 들었다. 'AAA'경로에서 막혔지만, 실제로는 더 깊이 들어가다 막혔을 경우가 많을 것이다. 이 때까지 탐색했던 경로는 그럼 어떻게 다시 재사용하게 되는지 좀 더 고민해보기로 했다.
AAA에 추가로 노드들을 더 연결해봤고, 마찬가지로 스택에 구현한 뒤, 더 이상 진행할 수 없고, 간선이 남아 있을 경우, pop 하였다. 다시 ICN까지 돌아와서 다음 경로를 살피니, 답이 이어졌다.
