학습 주제

학습 내용

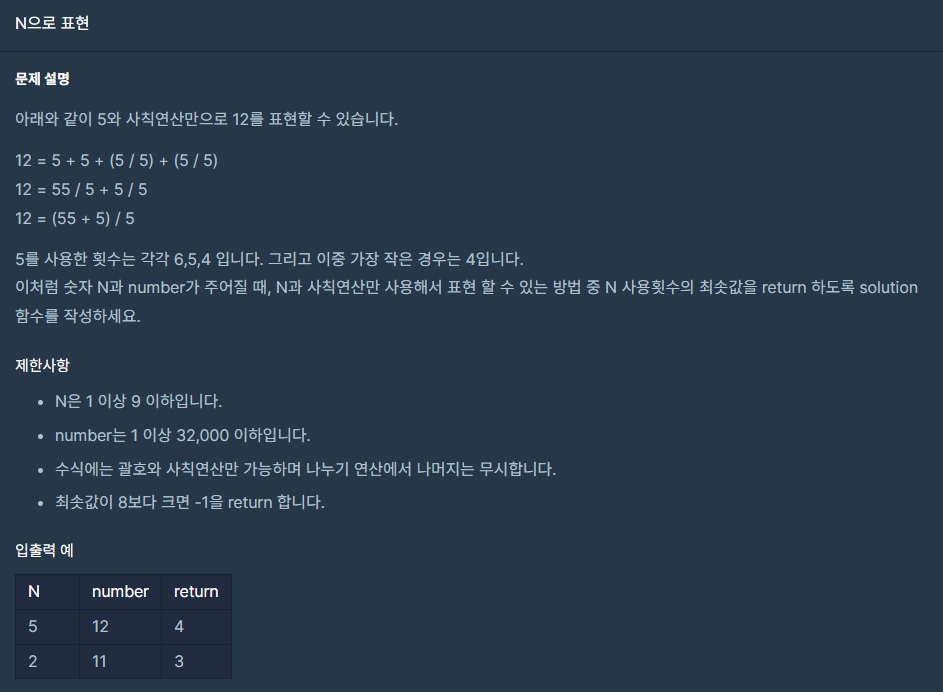
문제

알고리즘

• 1회부터 8회까지 N을 사용한 경우의 수가 담긴 집합 리스트 생성

• 중복을 허용하지 않게 하기 위해 set() 사용

• s = [set() for x in range(8)]

• 각 set에 N을 n회 반복한 값을 미리 집어넣음

• N(3)의 경우, N*3, N(1) 사칙연산 N(2), N(2) 사칙연산 N(1)임. 일반화 하면

• N(n)의 경우, N*n, N(1) 사칙연산 N(n-1), ..., N(n-1) 사칙연산 N(1)

• set을 사용했기 때문에 중복은 걸러짐.

• i를 1부터 7까지 반복을 함 i는 N(n)의 경우의 수를 하나씩 구해나가는 과정

• j를 i번째까지 순회. N(n)을 구하기 위한 N(1) ~ N(n-1)을 구해나가는 과정

• op1을 s[j]를 순회함. N(1) ~ N(n-1) 순으로 순회

• op2를 s[i - j - 1]을 순회함 N(n-1) ~ N(1) 순으로 순회

• 나눗셈은 나머지를 제외하므로 // 사용

• for i 순회 중, N(i+1) 내에 number가 있을 경우 i+1 리턴

• 모든 for 문 순회를 마치고 나서도 못 찾을 경우, answer -1 리턴

• 추가. 주어진 N과 얻고자하는 수 number가 같을 경우, 이때 1을 리턴 (테스트 8 통과)

내 풀이

def solution(N, number):
    if N == number:
        return 1
    
    s = [set() for x in range(8)]
    for i, x in enumerate(s, start=1):
        x.add(int(str(N)*i))
    for i in range(1, len(s)):
        for j in range(i):
            for op1 in s[j]:
                for op2 in s[i - j - 1]:
                    s[i].add(op1 + op2)
                    s[i].add(op1 - op2)
                    s[i].add(op1 * op2)
                    if op2 != 0:
                        s[i].add(op1 // op2)
        if number in s[i]:
            answer = i + 1
            break
    else:
        answer = -1
    return answer

어려운 점

지난 문제들에 비해 확실히 어렵다는 생각이 많이 들며 수업을 들었는데 lv 3 문제였다. for문을 2개까지 돌리는 것은 익숙하나, 4개를 돌리려고 하니 과부하가 왔다. 파이썬 튜터를 적극적으로 사용해서 코드가 어떻게 동작하는지 익숙해질 때까지 돌려보려고 한다. 아직도 0, n-1 등 1개 차이의 숫자가 헷갈린다.