학습 주제
동적계획법

학습 내용

동적계획법 (Dynamic Programming)

문제의 답인지를 확인하기 위해서 탐색해야되는 범위를 (solution space) 어떤 부분을 탐색할꺼냐 라는 것을 진전하면서 동적으로 결정한다.

처음에 다 크기를 짜놓는 것이 아니라, 부분 문제를 풀어가면서, 다음 단계에서 풀어야할 문제의 범위를 정해나감.

동적계획법 (Dynamic Programming)의 적용 예

피보나치 수열 n = n-1 + n-2 의 대표적인 재귀적인 수열
같은 인자를 재귀함수로 여러번 호출한다는 단점이 있음. 결국 f(1)과 f(0)를 여러번 호출해서 볼러내게 됨.

복잡도: 지수함수의 형태

부분해를 구한다. f(2) = f(1) + f(0)
피보나치도 부분해의 조합으로 푸는 문제.

주어진 수에 비례해서 복잡도가 정해짐.

Knapsack Problem
재귀적인 문제로 풀 수 있음.

• 어떤 하나의 아이템을 담고, 나머지 허용하는 양을 크게 채움.

문제 보기

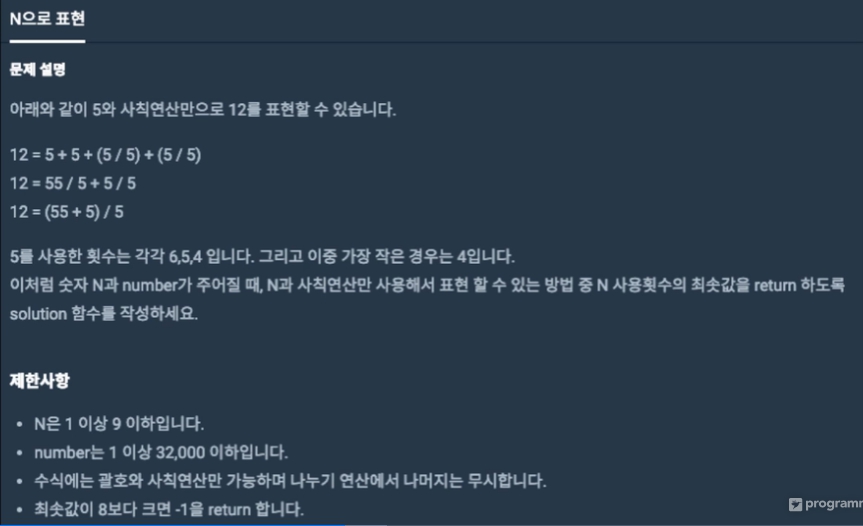
• 최솟값이 8보다 크면 -1 return 8까지 사용해서도 안나올꺼 같으면 바로 -1
  

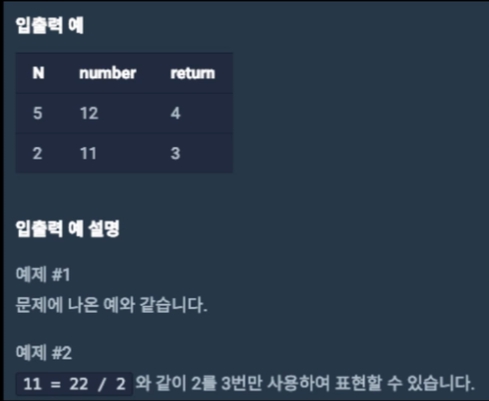
문제의 해결 - 동적계획법으로 설계

반복해 나가다가, 원하는 답에 도달하면 도출

N을 한번 사용해서 만들 수 있는 경우는 5 1개이나
2번째부터 1번 이용한 것을 사칙연산 또는 연결을 통해 만들어 낼 수 있음

• 더하기나 곱하기는 상관없으나, 빼기와 나눗셈은 순서에 값 영향을 받음
  
  3번은 1번 사용과 2번사용의 조합으로 만들어낼 수 있음. 겹치는 값은 포함하지 않도록 set 집합으로 표현함
  
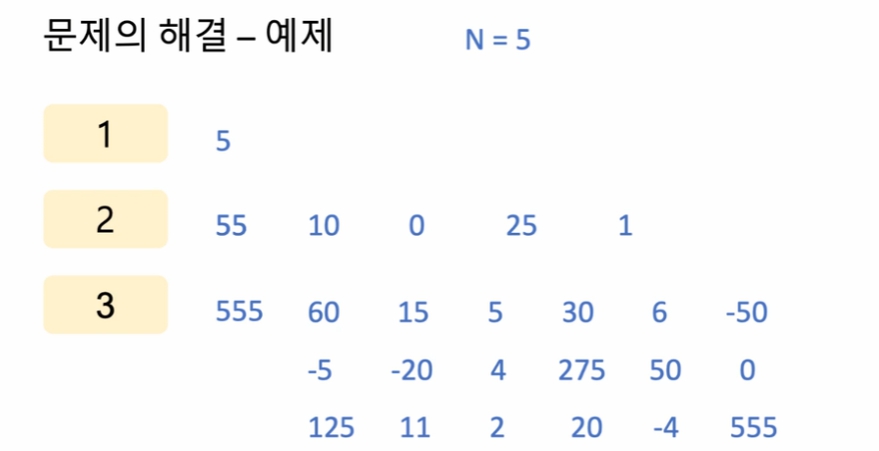
  3번 사용시, 경우의 수는 19개가 됨.
  
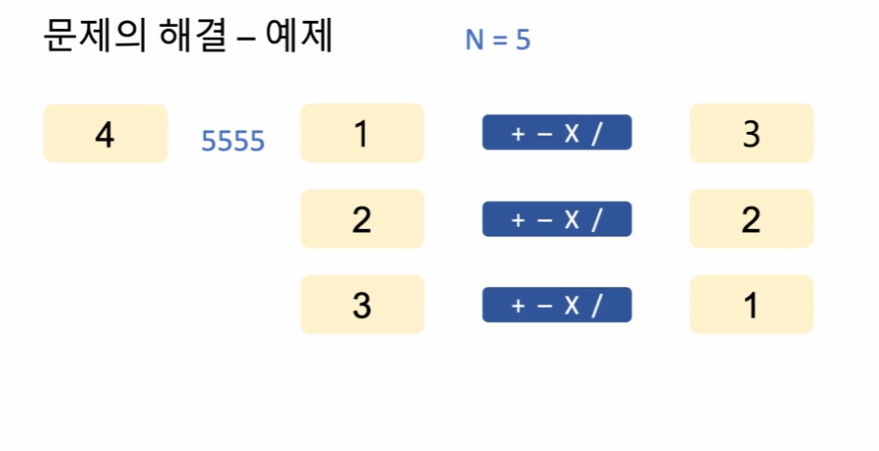
  4번 사용의 경우,

일반화를 할 경우

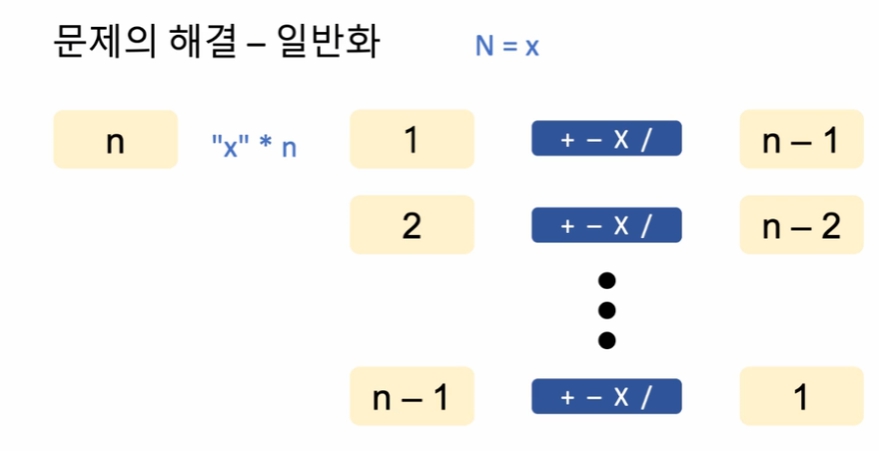
n -1 까지의 부분문제의 답을 알고 있다고 가정하고,
n 회 사용한다고 하면,

• "x"*n 처럼 5555
• 1과 n-1의 조합, 2와 n-2의 조합, n-1과 1의 조합의 중복되지 않는 경우의 합이다.

이 외에 괄호도 사용할 수 있음. 또는 여러 수식의 결과도 조합으로 가능함.
n이 커질 수록 조합의 수는 엄청나게 많아짐.

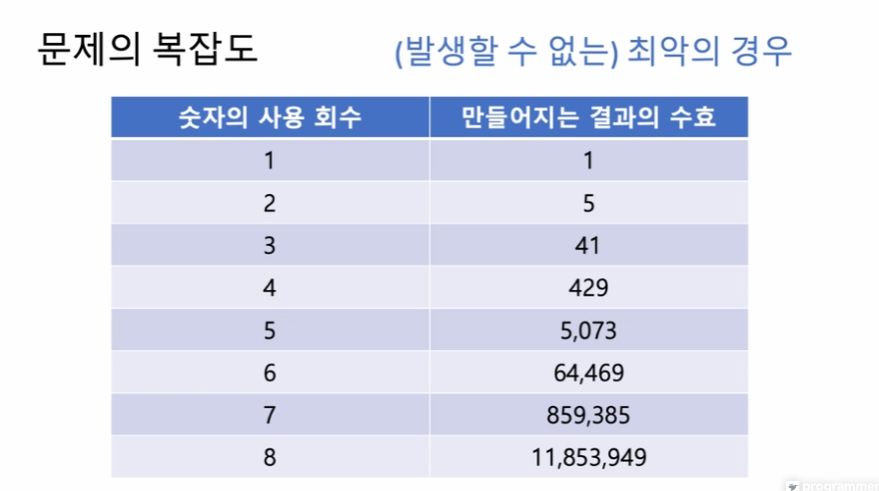
2의 경우
55, 5(사칙연산)5 총 5개
겹치는 것도 포함됨

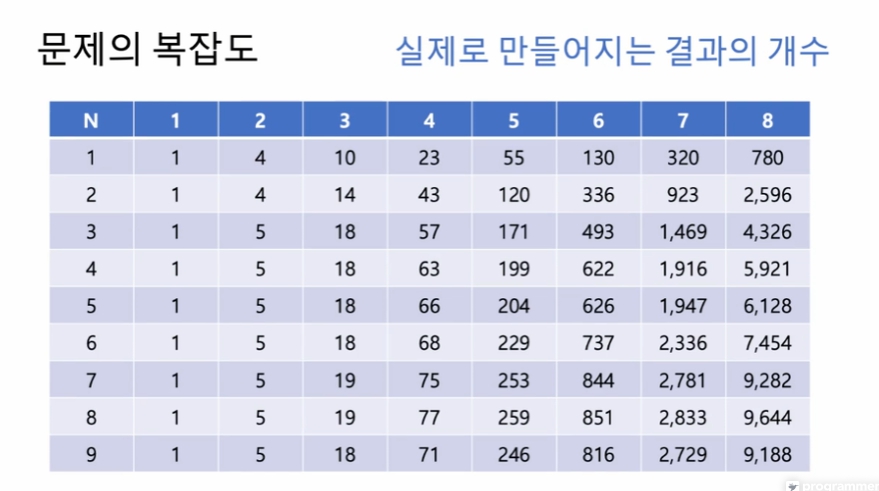
어느 수를 사용했느냐에 따라 연산 결과가 달라짐.
세로는 어떤 N.
가로는 횟수

요약

알고리즘이 진행함에 따라,