학습 주제
탐욕법을 이용한 문제 풀이

학습 내용

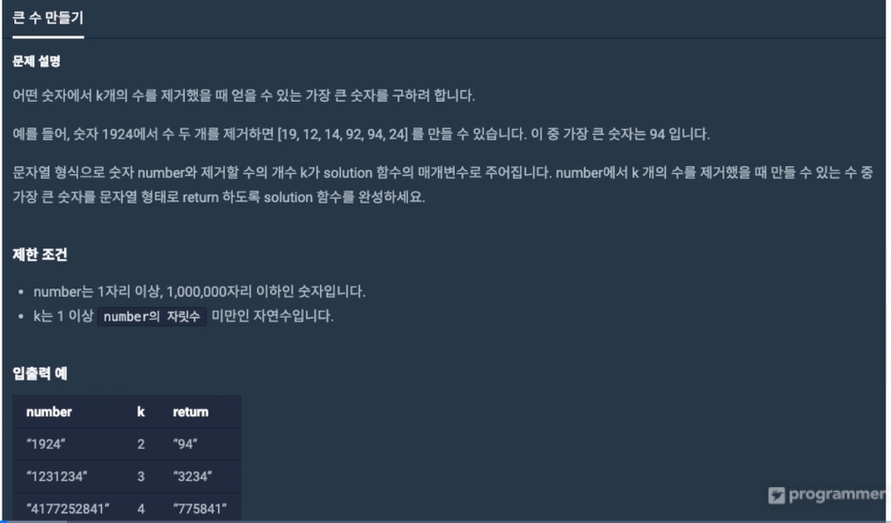
숫자가 클 수 있으므로 문자열로 주어지고 답도 문자열로 내야함
numbers는 최대 백만자리 (큰 숫자)

입출력 예 2
"1231234", 3, "3234"
~~답을 보면 이상하다. 사람이 풀었을 때 3개의 숫자를 빼고 그 중 가장 큰 수를 조합해 낸다면
"4332"가 가장 큰 수가 되어야 할 것이다. 그러나 답은 "3234"로 작은 숫자이다.
~~
제거만 할 수 있고, 원래 숫자의 배열은 조합할 수 없다. 앞에서 부터 두 수를 비교하며 작을경우 빼고, 작지 않을 경우 다음 숫자를 제거한다.
입출력 예 3
"4177252841", 4, "775841"
~~nubmer에서 가장 작은 숫자 4개 제거. 1, 1, 2, 2
남은 숫자는 "4775841" 내림차순하면 "7785441"
마찬가지로 제일 큰 경우보다 다소 작은 것을 알 수 있다.
~~
1,4,2,2 순으로 제거한다. 앞에서 부터 2자리씩 비교하며 진행, 두 숫자가 같을 경우 넘어감.
"7784551"

탐욕법은 지역적인 상황에서 최선의 선택을 해 답안을 구해내는 방법이다. 완벽하진 않지만 효율이 좋은 편이다. 이정도까지 답과 문제 상황을 이해 하고 강의를 이어서 듣는다.

큰 수 만들기 - 원칙

빼는 것이 아닌 우선적으로 큰 수를 골라담는다.
예제들을 다시 살펴보면,

눈으로 보았을 때, 1,2가 작아, 9, 4를 담는다.

뒤에 남는걸 빼도 이득이 되지 않음. 앞에서부터 작은 것들을 제외하는게 이득임.

-> 순차적인 알고리즘으로 어떻게 만들어 나갈지 깊게 고민

큰 수 만들기 - 방법

수가 매우 커질경우 눈으로 직관적으로 풀기는 어려움.

처음에는 그냥 4를 담음

그다음 숫자인 1도 그대로 담음

7이 왔을 때 7이 앞에 오는게 유리해 보임. 제거할 수 있는 수는 4개이므로 일단 1을 제거.

7이 4보다도 크니까 4도 빼고 이를 별도로 기록함.

5가 왔을 때, 앞에 있는 2보다 크고, 아직 뺄 수 있는 갯수가 남아있으므로 2를 빼고 5를 앞으로 당겨 붙힘. 카운트함.

5는 7보다는 작음. 그럼 더는 볼 필요가 없음.

2의 등장. 5보다 작음으로 그대로 둠.

8의 등장 앞의 2보다 크므로 2를 제거하고 8을 당겨줌. 카운트 올라감. 카운트 4개로 더 이상 뺄 수 없으므로 종료.

주의할 점

위 숫자는 이미 가장 큰 수부터 정렬되어있다. 위의 알고리즘대로라면 numbers에 대한 순회를 마치고도 제거할 수 가 없다고 판단하여 뺀 수가 없게 된다. 이때에는 가장 뒤에서 제거할 수만큼 제거했을 때가 가장 큰 경우의 수가 된다.
따라서 순회를 마치고 난 후, 아직도 빼야할 갯수가 남아있다면, 그 갯수만큼 뒤에서 빼준다.

알고리즘 설계 -> 구현

알고리즘의 복잡도

가장 무식한 방법은? 모든 조합을 나열하고 고르기.
-> number, k 모두 클수록 경우의 수가 매우 많아짐.

O(n^2)로 오해할 수 있음.
각 자리수가 더해지는 것 1번, 빠지는 것 1번. 2*n에 가까움.

탐욕법 (Greedy Approach)

최적성 = 품질

현재 상태에서 최선이 누적되어 최적해가 됨.

모든 조사를 하지 않더라도, 한 방향으로 진행해도 최적의 답을 구할 수 있는 문제들을 알아낼 수 있어야 함.

어려운 점

차후 문제를 풀 때 탐욕법을 적용할 수 있는지, 또 탐욕법이 놓칠 수 있는 예외를 알아보고 그에 대한 예외처리를 할 수 있는지 고민.