문제
조기 졸업을 꿈꾸는 종욱이는 요즘 핫한 딥러닝을 공부하던 중, 이미지 처리에 흔히 쓰이는 합성곱 신경망(Convolutional Neural Network, CNN)의 풀링 연산에 영감을 받아 자신만의 풀링을 만들고 이를 222-풀링이라 부르기로 했다.
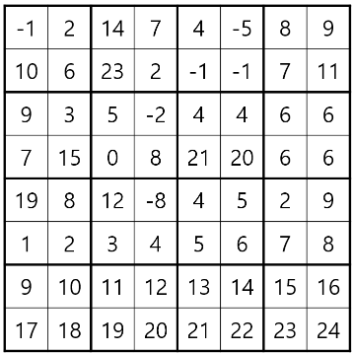
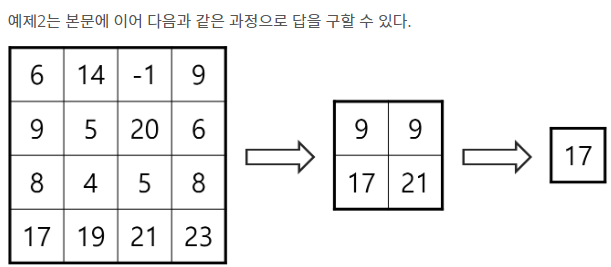
다음은 8×8 행렬이 주어졌다고 가정했을 때 222-풀링을 1회 적용하는 과정을 설명한 것이다
행렬을 2×2 정사각형으로 나눈다.
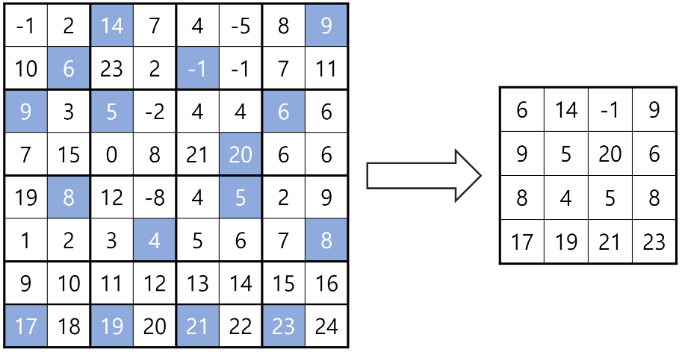
각 정사각형에서 2번째로 큰 수만 남긴다. 여기서 2번째로 큰 수란, 정사각형의 네 원소를 크기순으로 a4 ≤ a3 ≤ a2 ≤ a1 라 했을 때, 원소 a2를 뜻한다.
2번 과정에 의해 행렬의 크기가 줄어들게 된다.
종욱이는 N×N 행렬에 222-풀링을 반복해서 적용하여 크기를 1×1로 만들었을 때 어떤 값이 남아있을지 궁금해한다.
랩실 활동에 치여 삶이 사라진 종욱이를 애도하며 종욱이의 궁금증을 대신 해결해주자.
입출력 예
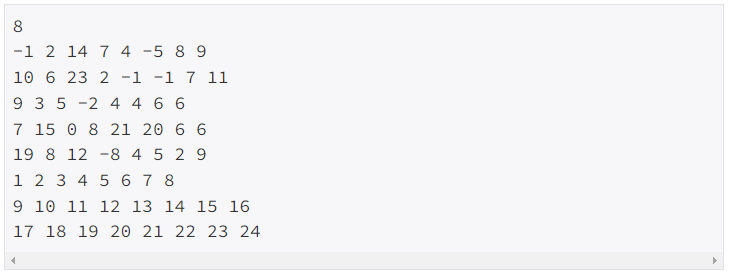
예제 입력 1
예제 출력 1
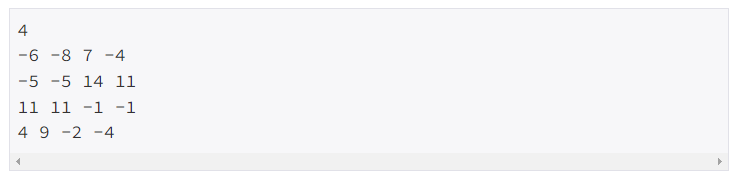
예제 입력 2
예제 출력 2
힌트
풀이
저는 활용할 수 있는 라이브러리가 많지 않아 if문을 12번이나 써서 약간 노가다(?)느낌으로 풀었습니다. 그래도 문제의 난이도는 그렇게 높지 않았다고 생각합니다. 비교를 하는 compare함수와 비교를 진행한 후 좌표를 옮기며 compare함수를 호출하여 확인하는 square함수를 사용하여 문제를 풀었습니다.
#include <iostream> #include <vector> #include <cmath> using namespace std; int square_size[1024][1024]; int compare(int a, int b, int c, int d) { if (a >= b && a >= c && a >= d) { if (b >= c && b >= d) return b; if (c >= b && c >= d) return c; else return d; } if (b >= a && b >= c && b >= d) { if (a >= c && a >= d) return a; if (c >= a && c >= d) return c; else return d; } if (c >= a && c >= b && c >= d) { if (a >= b && a >= d) return a; if (b >= a && b >= d) return b; else return d; } if (d >= a && d >= b && d >= c) { if (a >= b && a >= c) return a; if (b >= a && b >= c) return b; else return c; } } int square(int n, int x, int y) { if (n == 1) { return square_size[x][y]; } int new_size = n / 2; int a = square(new_size, x, y); int b = square(new_size, x, y + new_size); int c = square(new_size, x + new_size, y); int d = square(new_size, x + new_size, y + new_size); return compare(a, b, c, d); } int main() { int n; cin >> n; for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { cin >> square_size[i][j]; } } int result = square(n, 0, 0); cout << result; return 0; }
코드해석
첫 번째로 main함수를 보게되면 별게 없습니다. 그냥 2중 for문 사용해서 square_size의 배열 돌고, square함수에 매개변수 (n, 0, 0) 넣어서 result에 넣어주고 출력하는것 밖에 없습니다.
두 번째로는 compare함수를 보게되면 2x2행렬의 (0, 0) (1, 0) (0, 1) (1, 1)의 원소값을 각각 a, b, c, d로 만들어주고 이를 각각 비교하여 각각의 return값을 정해주었습니다. 처음으로 나오는 if문을 한번 본다면
if (a >= b && a >= c && a >= d) { if (b >= c && b >= d) return b; if (c >= b && c >= d) return c; return d; }로 표현하였는데 이는 두번째로 큰 수를 리턴하기 위해 a가 가장 큰 경우를 먼저 고르고 거기서 b가 c, d보다 크다면 b를 return, c가, b, d보다 크다면 c를 return, 그리고 나머지 경우는 d를 리턴해 주는 코드로 보시면 됩니다. 이렇게 각각의 경우의 수를 체크하여 비교하는 함수는 square함수에서 다시 사용됩니다.
세 번째로 square함수를 보겠습니다. 전 두 문제와 마찬가지로 2차원 평면에서 x축과 y축으로 이동하기위해 첫 입력값을 n과 x축과 y축으로의 이동을 위한 x, y를 매개변수로 설정하고 이를 main함수에서 받을 수 있도록 선언하였습니다.
이후 if문을 사용하여 n == 1일 경우에는 1x1행렬이 되어 그냥 숫자가 하나이므로 입력된 숫자값 하나를 출력해주게 됩니다.
그 다음으로 나오는int new_size의 경우에는 원래 행렬의 크기를 반으로 나누어 주는 역할을 진행합니다. 이는 결국 1x1의 행렬의 크기로 만들어 리턴하기 위해 사용됩니다.
이후 square함수는 다음과 같이 진행됩니다!int square(int n, int x, int y) { if (n == 1) { return square_size[x][y]; } int new_size = n / 2; int a = square(new_size, x, y); int b = square(new_size, x, y + new_size); int c = square(new_size, x + new_size, y); int d = square(new_size, x + new_size, y + new_size); return compare(a, b, c, d); }
new_size = 4/2 = 2 int a = square(2, 0, 0): new_size = 1, int a = square(1, 0, 0): square_size[0][0] 값인 -6 반환 new_size = 1, int b = square(1, 0, 1): square_size[0][1] 값인 -8 반환 new_size = 1, int c = square(1, 1, 0): square_size[1][0] 값인 -5 반환 new_size = 1, int d = square(1, 1, 1): square_size[1][1] 값인 -5 반환 compare(a, b, c, d) 실행: 두 번째로 큰 값인 -6 반환 int a에 -6 저장 new_size = 2, int b = square(2, 0, 2): new_size = 1, int a = square(1, 0, 2): square_size[0][2] 값인 7 반환 new_size = 1, int b = square(1, 0, 3): square_size[0][3] 값인 -4 반환 new_size = 1, int c = square(1, 1, 2): square_size[1][2] 값인 14 반환 new_size = 1, int d = square(1, 1, 3): square_size[1][3] 값인 11 반환 compare(a, b, c, d) 실행: 두 번째로 큰 값인 11 반환 int b에 11 저장 new_size = 2, int c = square(2, 2, 0): new_size = 1, int a = square(1, 2, 0): square_size[2][0] 값인 11 반환 new_size = 1, int b = square(1, 2, 1): square_size[2][1] 값인 11 반환 new_size = 1, int c = square(1, 3, 0): square_size[3][0] 값인 4 반환 new_size = 1, int d = square(1, 3, 1): square_size[3][1] 값인 9 반환 compare(a, b, c, d) 실행: 두 번째로 큰 값인 11 반환 int c에 11 저장 new_size = 2, int d = square(2, 2, 2): new_size = 1, int a = square(1, 2, 2): square_size[2][2] 값인 -1 반환 new_size = 1, int b = square(1, 2, 3): square_size[2][3] 값인 -1 반환 new_size = 1, int c = square(1, 3, 2): square_size[3][2] 값인 -2 반환 new_size = 1, int d = square(1, 3, 3): square_size[3][3] 값인 -4 반환 두 번째로 큰 값인 -1 반환 int d에 -1 저장그러면 최종적으로 compare(-6, 11, 11, -1)이 되며 여기서 다시 11을 호출하여 최종 결과값을 11 이 됩니다.
세 번째 알고리즘 풀이인데, 난이도가 점점 내려가는거 같아서 서서히 올려가도록 해야겠네요...ㅎㅎ