[제로베이스 데이터 취업 스쿨 15기] 3주차 (기초수학/문제풀이)

김지환·2023년 5월 15일
python
0
post-thumbnail

3주차: 5/15/2023 - 5/21/2023


Numbers


Divisors and primes

  • Divisor of an integer n: an integer m that may be multiplied by some integer to produce n
# Divisor
inputNumber = int(input('Input an integer greater than 0: '))

for number in range(1, inputNumber+1):
    if inputNumber % number == 0:
        print('Divisor of {}: {}'.format(inputNumber, number))
  • Prime: a natural number greater than 1 that is not a product of two smaller natural numbers
# Prime
inputNumber = int(input('Input an integer greater than 0: '))

for number in range(2, inputNumber+1):
    flag = True
    for n in range(2, number):
        if number % n == 0:
            flag = False
            break

    if flag:
        print('{}: prime'.format(number))
    else:
        print('{}: \t\t composite'.format(number))
  • Prime factorization: decomposition of a positive integer into a product of smaller primes
# Prime factors

inputNumber = int(input('Input an integer greater than 1: '))

n = 2
while n <= inputNumber:
    if inputNumber % n == 0:
        print('Prime factor: {}'.format(n))
        inputNumber /= n
    else:
        n += 1

# Prime factorization

inputNumber = int(input('Input an integer greater than 1: '))

n = 2
searchNumbers = []

while n <= inputNumber:
    if inputNumber % n == 0:
        print('Prime factor: {}'.format(n))
        if searchNumbers.count(n) == 0:
            searchNumbers.append(n)
        elif searchNumbers.count(n) == 1:
            searchNumbers.remove(n)
        inputNumber /= n
    else:
        n += 1

print('searchNumbers: {}'.format(searchNumbers))
  • Greatest common divisor (GCD): GCD of two or more integers, which are not all zero, is the largest positive integer that divides each of the integers
# GCD of two numbers

num1 = int(input('Input an integer greater than 1: '))
num2 = int(input('Input an integer greater than 1: '))

gcd = 0

for i in range(1, num1+1):
    if num1 % i == 0 and num2 % i == 0:
        print('Common divisor: {}'.format(i))
        gcd = i

print('Greatest common divisor: {}'.format(gcd))

# GCD of three numbers

num1 = int(input('Input an integer greater than 1: '))
num2 = int(input('Input an integer greater than 1: '))
num3 = int(input('Input an integer greater than 1: '))

gcd = 0

for i in range(1, num1+1):
    if num1 % i == 0 and num2 % i == 0 and num3 % i == 0:
        print('Common divisor: {}'.format(i))
        gcd = i

print('Greatest common divisor: {}'.format(gcd))

# Euclidean algorithm

num1 = int(input('Input an integer greater than 1: '))
num2 = int(input('Input an integer greater than 1: '))

temp1 = num1; temp2 = num2

while temp2 > 0:
    temp = temp2
    temp2 = temp1 % temp2
    temp1 = temp

print('GCD of {} and {}: {}'.format(num1, num2, temp1))

for n in range(1, temp1+1):
    if temp1 % n == 0:
        print('Common divisor of {} and {}: {}'.format(num1, num2, n))
  • Least common multiple (LCM): LCM of two integers a and b is the smallest positive integer that is divisible by both a and b
# LCM of two numbers

num1 = int(input('Input an integer greater than 1: '))
num2 = int(input('Input an integer greater than 1: '))

gcd = 0

for i in range(1, num1+1):
    if num1 % i == 0 and num2 % i == 0:
        print('Common divisor: {}'.format(i))
        gcd = i

print('Greatest common divisor: {}'.format(gcd))

lcm = (num1 * num2) // gcd
print('Least common multiple: {}'.format(lcm))

# LCM of three numbers

num1 = int(input('Input an integer greater than 1: '))
num2 = int(input('Input an integer greater than 1: '))
num3 = int(input('Input an integer greater than 1: '))

gcd = 0

for i in range(1, num1+1):
    if num1 % i == 0 and num2 % i == 0:
        print('Common divisor: {}'.format(i))
        gcd = i

print('Greatest common divisor: {}'.format(gcd))

lcm = (num1 * num2) // gcd
print('Least common multiple: {}'.format(lcm))

newNum = lcm

for i in range(1, newNum+1):
    if newNum % i == 0 and num3 % i == 0:
        gcd = i

print('Greatest common divisor: {}'.format(gcd))

lcm = (newNum * num3) // gcd
print('Least common multiple: {}'.format(lcm))

# Exercise

ship1 = 3; ship2 = 4; ship3 = 5
gcd = 0

for i in range(1, ship1+1):
    if ship1 % i == 0 and ship2 % i == 0:
        gcd = i

print('GCD: {}'.format(gcd))

lcm = (ship1 * ship2) // gcd
print('LCM of {} and {}: {}'.format(ship1, ship2, lcm))

newDay = lcm

for i in range(1, newDay+1):
    if newDay % i == 0 and ship3 % i == 0:
        gcd = i

print('GCD: {}'.format(gcd))

lcm = (newDay * ship3) // gcd
print('LCM of {} and {}: {}'.format(ship2, ship3, lcm))
  • Base: the number of unique digits, including the digit zero, used to represent numbers
dNum = 30

print('Binary: {}'.format(bin(dNum)))
print('Octal: {}'.format(oct(dNum)))
print('Hexadecimal: {}'.format(hex(dNum)))

print('Binary: {}'.format(type(bin(dNum))))
print('Octal: {}'.format(type(oct(dNum))))
print('Hexadecimal: {}'.format(type(hex(dNum))))

print('Binary: {}'.format(format(dNum, '#b')))
print('Binary: {}'.format(format(dNum, '#o')))
print('Binary: {}'.format(format(dNum, '#x')))

print('{0:#b}, {0:#o}, {0:#x}'.format(dNum))

print('Binary: {}'.format(format(dNum, 'b')))
print('Binary: {}'.format(format(dNum, 'o')))
print('Binary: {}'.format(format(dNum, 'x')))

print('Binary (0b11110) -> Decimal ({})'.format(int('0b11110', 2)))
print('Octal (0o36) -> Decimal ({})'.format(int('0o36', 8)))
print('Hexadecimal (0x1e) -> Decimal ({})'.format(int('0x1e', 16)))

Exercises

import random

rNum = random.randint(100, 1000)
print(f'rNum: {rNum}')

for num in range(1, rNum+1):

    primeFactor = 0

    # Divisor
    if rNum % num == 0:
        print(f'[Divisor]: {num}')
        primeFactor += 1

    # Prime
    if num != 1:
        flag = True
        for n in range(2, num):
            if num % n == 0:
                flag = False
                break
        if flag:
            print(f'[Prime]: {num}')
            primeFactor += 1

    # Prime factor
    if primeFactor >= 2:
        print(f'[Prime factor]: {num}')
import random

rNum = random.randint(100, 1000)
print(f'rNum: {rNum}')

primeFactorList = []

n = 2
while n <= rNum:
    if rNum % n == 0:
        print(f'Prime factor: {n}')
        primeFactorList.append(n)
        rNum /= n
    else:
        n += 1

print(f'primeFactorList: {primeFactorList}')

tempNum = 0
for p in primeFactorList:
    if tempNum != p:
        print(f'{p}\'s count: {primeFactorList.count(p)}')
        tempNum = p
        
import random

rNum1 = random.randint(100, 1000)
rNum2 = random.randint(100, 1000)

print(f'rNum1: {rNum1}')
print(f'rNum2: {rNum2}')

maxNum = 0

for n in range(1, min(rNum1, rNum2)+1):
    if rNum1 % n == 0 and rNum2 % n == 0:
        print(f'Common divisor: {n}')
        maxNum = n

print(f'GCD: {maxNum}')

if maxNum == 1:
    print(f'{rNum1} and {rNum2} are coprime')
import random

rNum1 = random.randint(100, 1000)
rNum2 = random.randint(100, 1000)

print(f'rNum1: {rNum1}')
print(f'rNum2: {rNum2}')

maxNum = 0

for n in range(1, min(rNum1, rNum2)+1):
    if rNum1 % n == 0 and rNum2 % n == 0:
        print(f'Common divisor: {n}')
        maxNum = n

print(f'GCD: {maxNum}')

minNum = (rNum1 * rNum2) // maxNum
print(f'LCM: {minNum}')

Sequences


  • Sequence: an enumerated collection of objects in which repetitions are allowed and order matters
  • Arithmetic sequence: a sequence of numbers such that the difference from any succeeding term to its preceding term remains constant throughout the sequence
    - an=a1+(n−1)∗da_n = a_1 + (n-1) * d where dd is the common difference
    - an−1+an+12=an\frac{a_{n-1} + a_{n+1}}{2} = a_n
    - sn=n(a1+an)2s_n = \frac{n(a_1 + a_n)}{2}
# Find the nth term: using the common difference

inputA1 = int(input('Input first term a1: '))
inputD = int(input('Input common difference d: '))
inputN = int(input('Input n: '))

valueN = 0
n = 1
while n <= inputN:

    if n == 1:
        valueN = inputA1
        print('Value of the {}th term: {}'.format(n, valueN))
        n += 1
        continue

    valueN += inputD
    print('Value of the {}th term: {}'.format(n, valueN))
    n += 1

print('Value of the {}th term: {}'.format(inputN, valueN))

# Find the nth term: using the formula an = a1 + (n-1)d

inputA1 = int(input('Input first term a1: '))
inputD = int(input('Input common difference d: '))
inputN = int(input('Input n: '))

valueN = 0

valueN = inputA1 + (inputN - 1) * inputD
print('Value of the {}th term: {}'.format(inputN, valueN))
# Find the sum: using the common difference

inputA1 = int(input('Input first term a1: '))
inputD = int(input('Input common difference d: '))
inputN = int(input('Input n: '))

valueN = 0
sumN = 0
n = 1
while n <= inputN:

    if n == 1:
        valueN = inputA1
        sumN = valueN
        print('Value of the sum of the first {} terms: {}'.format(n, sumN))
        n += 1
        continue

    valueN += inputD
    sumN += valueN
    print('Value of the sum of the first {} terms: {}'.format(n, sumN))
    n += 1

print('Value of the sum of the first {} terms: {}'.format(inputN, sumN))

# Find the sum: using the formula
#   - an = a1 + (n-1)d
#   - sn = n(a1 + an) / 2

inputA1 = int(input('Input first term a1: '))
inputD = int(input('Input common difference d: '))
inputN = int(input('Input n: '))

valueN = inputA1 + (inputN - 1) * inputD
sumN = inputN * (inputA1 + valueN) / 2
print('Value of the sum of the first {} terms: {}'.format(inputN, int(sumN)))
  • Geometric sequence: a sequence of non-zero numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio
    - an=a1∗rn−1a_n = a_1 * r^{n-1} where rr is the common ratio
    - an−1∗an+1=an2a_{n-1} * a_{n+1} = a_n^2
    - sn=a1∗(1−rn)1−rs_n = \frac{a_1*(1-r^n)}{1-r}
# Find the nth term: using the common ratio

inputA1 = int(input('Input first term a1: '))
inputR = int(input('Input common ratio r: '))
inputN = int(input('Input n: '))

valueN = 0

n = 1
while n <= inputN:

    if n == 1:
        valueN = inputA1
        print('Value of the {}th term: {}'.format(n, valueN))
        n += 1
        continue

    valueN *= inputR
    print('Value of the {}th term: {}'.format(n, valueN))
    n += 1

print('Value of the {}th term: {}'.format(inputN, valueN))

# Find the nth term: using the formula an = a1 * r^(n-1)

inputA1 = int(input('Input first term a1: '))
inputR = int(input('Input common ratio r: '))
inputN = int(input('Input n: '))

valueN = inputA1 * (inputR ** (inputN - 1))
print('Value of the {}th term: {}'.format(inputN, valueN))

# Find the sum: using the common ratio

inputA1 = int(input('Input first term a1: '))
inputR = int(input('Input common ratio r: '))
inputN = int(input('Input n: '))

valueN = 0
sumN = 0
n = 1

while n <= inputN:

    if n == 1:
        valueN = inputA1
        sumN += valueN
        print('Value of the sum of the first {} terms: {}'.format(n, sumN))
        n += 1
        continue

    valueN *= inputR
    sumN += valueN
    print('Value of the sum of the first {} terms: {}'.format(n, sumN))
    n += 1

print('Value of the sum of the first {} terms: {}'.format(inputN, sumN))

# Find the sum: using the formula sn = a1 * (1 - r^n) / (1 - r)

inputA1 = int(input('Input first term a1: '))
inputR = int(input('Input common ratio r: '))
inputN = int(input('Input n: '))

sumN = inputA1 * (1 - inputR ** inputN) / (1 - inputR)
print('Value of the sum of the first {} terms: {}'.format(inputN, int(sumN)))

# Exercise: arithmetic sequence

# an = a1 + (n - 1) * d
# sn = n * (a1 + an) / 2

inputA1 = int(input('Input first term a1: '))
inputD = int(input('Input common difference d: '))
inputN = int(input('Input n: '))

valueN = inputA1 + (inputN - 1) * inputD
sumN = inputN * (inputA1 + valueN) / 2
print('Value of the sum of the first {} terms: {}'.format(inputN, int(sumN)))

# Exercise: geometric sequence

# sn = a1 * (1 - r^n) / (1 - r)

inputA1 = int(input('Input first term a1: '))
inputR = int(input('Input common ratio r: '))
inputN = int(input('Input n: '))

sumN = inputA1 * (1 - inputR ** inputN) / (1 - inputR)
print('Value of the sum of the first {} terms: {}'.format(inputN, int(sumN)))
  • Difference sequence: a sequence that consists of terms that are differences of adjacent terms in another sequence
# a_n = {3, 7, 13, 21, 31, 43, 57}

inputA1 = int(input('Input first term a1: '))
inputAN = int(input('Input n of an: '))

inputB1 = int(input('Input first term a1: '))
inputBD = int(input('Input the common difference d for bn: '))

valueAN = 0
valueBN = 0

n = 1
while n <= inputAN:

    if n == 1:
        valueAN = inputA1
        valueBN = inputB1
        print('Value of {}th term of an: {}'.format(n, valueAN))
        print('Value of {}th term of bn: {}'.format(n, valueBN))
        n += 1
        continue

    valueAN += valueBN
    valueBN += inputBD
    print('Value of {}th term of an: {}'.format(n, valueAN))
    print('Value of {}th term of bn: {}'.format(n, valueBN))
    n += 1

print('Value of {}th term of an: {}'.format(inputAN, valueAN))
print('Value of {}th term of bn: {}'.format(inputAN, valueBN))

# bk = 2k + 2
# sn = n(b1 + bn) / 2
# s(n-1) = (n-1)(4 + 2(n-1) + 2) / 2 = (n-1)(2n + 4) / 2 = (n-1)(n+2) = n^2 + n - 2 = an - a1 = an - 3
# an = n^2 + n + 1

inputA1 = int(input('Input first term a1: '))
inputAN = int(input('Input n of an: '))

valueAN = inputAN ** 2 + inputAN + 1
print('Value of {}th term of an: {}'.format(inputAN, valueAN))
  • Fibonacci sequence: a sequence in which each number is the sum of the two preceding ones
inputN = int(input('Input n: '))

valueN = 0
sumN = 0

valuePreN2 = 0
valuePreN1 = 0

n = 1
while n <= inputN:
    if n == 1 or n == 2:
        valueN = 1
        valuePreN2 = valueN
        valuePreN1 = valueN

        sumN += valueN
        n += 1

    else:
        valueN = valuePreN2 + valuePreN1
        valuePreN2 = valuePreN1
        valuePreN1 = valueN
        sumN += valueN
        n += 1

print('Value of {}th term: {}'.format(inputN, valueN))
print('Sum of the first {} terms: {}'.format(inputN, sumN))
  • Factorial of a non-negative integer nn: the product of all positive integers less than or equal to nn
# Using the for loop
inputN = int(input('Input n: '))

result = 1
for n in range(1, inputN + 1):
    result *= n

print('{}!: {}'.format(inputN, result))

inputN = int(input('Input n: '))


# Using recursion
def factorialFun(n):
    if n == 1:
        return 1
    return n * factorialFun(n - 1)


print('{}!: {}'.format(inputN, factorialFun(inputN)))

# Using the math library
import math
inputN = int(input('Input n: '))
print('{}!: {}'.format(inputN, math.factorial(inputN)))
  • Group sequence: a sequence which exhibits a pattern when its terms are grouped

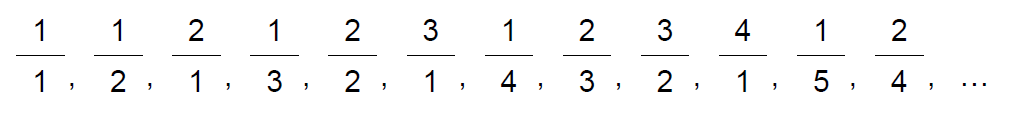
# Exercise 1

inputN = int(input('Input n: '))

flag = True
n = 1; nCnt = 1; searchN = 0

while flag:

    for i in range(1, n+1):
        if i == n:
            print('{} '.format(i), end='')
        else:
            print('{}, '.format(i), end='')

        nCnt += 1
        if nCnt > inputN:
            searchN = i
            flag = False
            break
    print()
    n += 1

print('{}th term: {}'.format(inputN, searchN))

# Exercise 2

inputN = int(input('Input n: '))

flag = True
n = 1; nCnt = 1; searchNC = 0; searchNP = 0
while flag:

    for i in range(1, n+1):
        if i == n:
            print('{}/{} '.format(i, (n-i+1)), end='')
        else:
            print('{}/{}, '.format(i, (n-i+1)), end='')

        nCnt += 1
        if nCnt > inputN:
            searchNC = i
            searchNP = n - i + 1
            flag = False
            break
    print()
    n += 1

print('{}th term: {}/{}'.format(inputN, searchNC, searchNP))

Exercises

# inputA1 = int(input('Input a1: '))
# inputD = int(input('Input d: '))
# inputN = int(input('Input n: '))

valueN = 0; sumN = 0

n = 1

while n <= inputN:

    if n == 1:
        valueN = inputA1
        sumN += valueN
        print('Value of the {}th term: {}'.format(n, valueN))
        print('Sum of the first {} terms: {}'.format(n, sumN))
        n += 1
        continue

    valueN += inputD
    sumN += valueN
    print('Value of the {}th term: {}'.format(n, valueN))
    print('Sum of the first {} terms: {}'.format(n, sumN))
    n += 1

print('Value of the {}th term: {}'.format(inputN, valueN))
print('Sum of the first {} terms: {}'.format(inputN, sumN))

# Formula

inputA1 = int(input('Input a1: '))
inputD = int(input('Input d: '))
inputN = int(input('Input n: '))

valueN = inputA1 + (inputN - 1) * inputD
print('Value of the {}th term: {}'.format(inputN, valueN))

sumN = inputN * (inputA1 + valueN) / 2
print('Sum of the first {} terms: {}'.format(inputN, int(sumN)))

# inputA1 = int(input('Input a1: '))
# inputR = int(input('Input r: '))
# inputN = int(input('Input n: '))

valueN = 0; sumN = 0

n = 1

while n <= inputN:

    if n == 1:
        valueN = inputA1
        sumN += valueN
        print('Value of the {}th term: {}'.format(n, valueN))
        print('Sum of the first {} terms: {}'.format(n, sumN))
        n += 1
        continue

    valueN *= inputR
    sumN += valueN
    print('Value of the {}th term: {}'.format(n, valueN))
    print('Sum of the first {} terms: {}'.format(n, sumN))
    n += 1

print('Value of the {}th term: {}'.format(inputN, valueN))
print('Sum of the first {} terms: {}'.format(inputN, sumN))

# Formula

inputA1 = int(input('Input a1: '))
inputR = int(input('Input r: '))
inputN = int(input('Input n: '))

valueN = inputA1 * (inputR ** (inputN - 1))
print('Value of the {}th term: {}'.format(inputN, valueN))

sumN = inputA1 * (1 - inputR ** inputN) / (1 - inputR)
print('Sum of the first {} terms: {}'.format(inputN, int(sumN)))
  • an={2,5,11,20,32,47,65,86,110,137,167,...}a_n = \{2, 5, 11, 20, 32, 47, 65, 86, 110, 137, 167, ...\} where a1=2a_1 = 2
    bn={3,6,9,12,...}b_n = \{3, 6, 9, 12, ... \} where b1=3b_1 = 3 and d=3d = 3
    bn=b1+(n−1)∗d=3+(n−1)∗3=3nb_n = b_1 + (n - 1) * d = 3 + (n-1) *3 = 3n
    ∑k=1n−1bk=an−a1\sum_{k=1}^{n-1}b_k = a_n - a_1
    ∑k=1nbk=n∗(b1+bn)/2\sum_{k=1}^{n}b_k = n * (b_1 + b_n) / 2
      ⟹  ∑k=1n−1bk=(n−1)∗(3+bn−1)/2\implies \sum_{k=1}^{n-1}b_k = (n-1) * (3 + b_{n-1}) / 2
    =(n−1)∗(3+3(n−1))/2=(3n2−3n)/2=an−2\hspace{2.2cm} = (n-1)*(3+3(n-1))/2 = (3n^2 - 3n) / 2 = a_n - 2
      ⟹  an=(3n2−3n)/2+2=(3n2−3n+4)/2\implies a_n = (3n^2 - 3n) / 2 + 2 = (3n^2 - 3n + 4) / 2
# Fibonacci

# an = a(n-2) + a(n-1)

inputN = int(input('Input n: '))

valueN = 0; sumN = 0

valuePreN2 = 0
valuePreN1 = 0

n = 1

while n <= inputN:
    if n == 1 or n == 2:
        valueN = 1
        valuePreN2 = valueN
        valuePreN1 = valueN
        sumN += valueN
        n += 1

    else:
        valueN = valuePreN2 + valuePreN1
        valuePreN2 = valuePreN1
        valuePreN1 = valueN
        sumN += valueN
        n += 1

print('Value of the {}th term: {}'.format(inputN, valueN))
print('Sum of the first {} terms: {}'.format(inputN, sumN))
flag = True

# Group number
n = 1

nCnt = 1; searchNC = 0; searchNP = 0

sumN = 0
while flag:

    for i in range(1, n+1):
        print('{}/{} '.format(i, n - i + 1), end='')

        sumN += i / (n - i + 1)
        nCnt += 1

        if sumN > 100:
            searchNC = i
            searchNP = n - i + 1
            flag = False
            break

    print()
    n += 1

print('Term at which the sum exceeds 100 for the first time: {}th term = {}/{}'.format(nCnt, searchNC, searchNP))
print('Sum of the values of which the sum exceeds 100 for the first time: {}'.format(round(sumN, 2)))

Probability


  • Permutation of a set: an arrangement of its members into a sequence or linear order, or if the set is already ordered, a rearrangement of its elements
    - nPr=n(n−1)(n−2)⋅⋅⋅(n−r+1)_nP_r = n(n-1)(n-2) \cdot\cdot\cdot (n-r+1) where 0<r<=n0 < r <= n
    - nPr=n!(n−r)!_nP_r = \frac{n!}{(n-r)!}
# Permutation

numN = int(input('Input numN: '))
numR = int(input('Input numR: '))

result = 1

for n in range(numN, (numN - numR), -1):
    print('n: {}'.format(n))
    result *= n

print('result: {}'.format(result))

# Circular permutation
#   - With repetition: n! / (n-r)!
#   - Without repetition: n! / r(n-r)!

n = int(input('Input the number of friends: '))
result = 1
for i in range(1, n):
    result *= i

print('result: {}'.format(result))
  • Combination of a set: a selection of items from a set that has distinct members, such that the order of selection does not matter (unlike permutations)
    - nCr=nPrr!=n!r!(n−r)!_nC_r = \frac{_nP_r}{r!} = \frac{n!}{r!(n-r)!} where 0<r<=n0 < r <= n
# Exercise 1

numN = int(input('Input numN: '))
numR = int(input('Input numR: '))

resultP = 1
resultR = 1
resultC = 1

for n in range(numN, numN-numR, -1):
    print('n: {}'.format(n))
    resultP *= n

print('resultP: {}'.format(resultP))

for n in range(numR, 0, -1):
    print('n: {}'.format(n))
    resultR *= n

print('resultR: {}'.format(resultR))

resultC = int(resultP / resultR)

print('resultC: {}'.format(resultC))

# Exercise 2

numN = int(input('Input numN: '))
numR = int(input('Input numR: '))

resultP = 1
resultR = 1
resultC = 1

for n in range(numN, numN-numR, -1):
    print('n: {}'.format(n))
    resultP *= n

print('resultP: {}'.format(resultP))

for n in range(numR, 0, -1):
    print('n: {}'.format(n))
    resultR *= n

print('resultR: {}'.format(resultR))

resultC = int(resultP / resultR)

print('resultC: {}'.format(resultC))

result = (1/resultC) * 100
print('{}%'.format(round(result, 2)))
  • Probability of an event: a number that indicates how likely the event is to occur
# 7C3 = 35
# 4C2 * 3C1 / 35 = 6 * 3 / 35 = 18/35

def proFun():
    numN = int(input('Input numN: '))
    numR = int(input('Input numR: '))

    resultP = 1
    resultR = 1
    resultC = 1

    for n in range(numN, numN-numR, -1):
        resultP *= n
    print('resultP: {}'.format(resultP))

    for n in range(numR, 0, -1):
        resultR *= n
    print('resultR: {}'.format(resultR))

    resultC = int(resultP / resultR)
    print('resultC: {}'.format(resultC))

    return resultC


sample = proFun()
print('sample: {}'.format(sample))

event1 = proFun()
print('event1: {}'.format(event1))

event2 = proFun()
print('event2: {}'.format(event2))

probability = event1 * event2 / sample
print('probability: {}%'.format(round(probability * 100, 2)))

Exercises

def proFun():

    numN = int(input('Input numN: '))
    numR = int(input('Input numR: '))

    resultP = 1
    resultR = 1
    resultC = 1

    # Permutation
    for n in range(numN, numN-numR, -1):
        resultP *= n
    print('resultP: {}'.format(resultP))

    # R!
    for n in range(numR, 0, -1):
        resultR *= n
    print('resultR: {}'.format(resultR))

    # Combination
    resultC = int(resultP / resultR)
    print('resultC: {}'.format(resultC))

    return resultC


sample = proFun()
print('sample: {}'.format(sample))

event1 = proFun()
print('event1: {}'.format(event1))

event2 = proFun()
print('event2: {}'.format(event2))

probability = event1 * event2 / sample
print('probability: {}%'.format(round(probability * 100, 2)))
profile
김지환
데이터 분석 공부하고 있습니다
이전 포스트

[제로베이스 데이터 취업 스쿨 15기] 2주차 (Python 중급/문제풀이)

다음 포스트

[제로베이스 데이터 취업 스쿨 15기] 4-1주차 (자료구조/문제풀이)

0개의 댓글