Dynamic Programming 동적 계획법

작은 부분 문제들부터 해결 한 후, 해당 해법을 활용해서 보다 큰 크기의 부분 문제를 해결. 최종적으로 전체 문제를 해결함

• 큰 문제를 작은 문제로 나누어 푸는 문제를 일컫는 말
• 상향식 접근법
  가장 최하위 해답을 구한 후 저장 하여 해다 결과 값을 이용해서 상위 문제를 풀어가는 방식
• 부분 문제는 중복되어 재활용
  한 번 계산한 문제는 다시 계산하지 않도록 하는 알고리즘

분할 정복

문제를 나눌 수 없을 때까지 나누어 작은 것을 풀고 다시 합병하여 문제의 답을 얻는 알고리즘

• 하향식 접근법
  상위의 해답을 구하기 위해 아래로 내려가면서 하위의 답을 구하는 방식
  주로 재귀함수로 구현
• 부분 문제 서로 중복되지 않음
• 공통점 : 가장 작은 단위부터 분할
• 차이점
  • 부분 문제 중복 : DP는 중복되어 재활용, 분할 정복은 중복되지 않음
  • Memoization : DP는 사용, 분할 정복은 사용하지 않음

동작

• Memoization 기법 사용
  프로그램 실행 시 이전에 계산한 값을 저장하여 다시 계산하지 않도록 전체 실행 속도를 빠르게 하는 기술

조건

• 최적 부분 구조 (Optimal Substructure)
  큰 문제를 작은 문제로 나눌 수 있고, 작은 문제의 답을 모아 큰 문제를 해결할 수 있는 경우를 의미
• 중복되는 부분 문제 (Overlapping Subproblem)
  동일한 작은 문제를 반복적으로 해결해야 하는 경우

😆 DP에서 Dynamic은 별다른 의미가 없다. 알고리즘을 만든 사람도 멋있다는 이유로 Dynamic이란 단어를 프로그래밍에 결합했다.

피보나치 수열

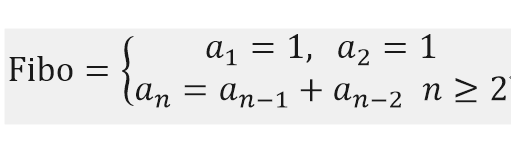
1. Memoization + 반복

def fibo_dp(num):
	cache = [0 for index in range(num+1)]
    cache[0] = 0
    cache[1] = 1
    
    for index in range(2, num + 1):
    	cache[index] = cache[index-1] + cache[index -2]
    return cache[num]

2. 재귀 함수

def fibo(x):
    if x == 1 or x == 2:
        return 1
    return fibo(x - 1) + fibo(x - 2)

💛 Tip

• 주어진 문제가 DP 유형인지 파악하는 것이 중요
  • 먼저 그리디, 시뮬레이션, 완전탐색 등의 알고리즘으로 문제를 풀 수 있는지 검토한 후 풀 수 없다고 생각이 들면 DP를 사용해보자!
• 수열은 배열이나 리스트로 표현할 수 있다고 했는데, 메모이제이션은 때에 따라서 다른 자료형, 예를 들어 딕셔너리 자료형을 이용할 수도 있다. --> 사전 - 자료형은 수열처럼 연속적이지 않을 때 유용하다.
• DP를 사용할 때, 일단 단순히 재귀 함수로 비효율적인 프로그램을 작성한 뒤에 (Top-Down) 작은 문제에서 구한 답이 큰 문제에서 그대로 사용될 수 있으면, 즉 메모이제이션을 적용할 수 있으면 코드를 개선하는 방법도 좋은 방법이다.
  • 위의 피보나치 수열의 예제 코드처럼 재귀 함수를 작성한 뒤에 나중에 메모이제이션 기법을 적용해 소스코드를 수정하는 것도 좋다!!

[참고]

• https://velog.io/@kimdukbae/%EB%8B%A4%EC%9D%B4%EB%82%98%EB%AF%B9-%ED%94%84%EB%A1%9C%EA%B7%B8%EB%9E%98%EB%B0%8D-Dynamic-Programming