<Baekjoon> #11060 Dynamic Programming_Jump Jump c++

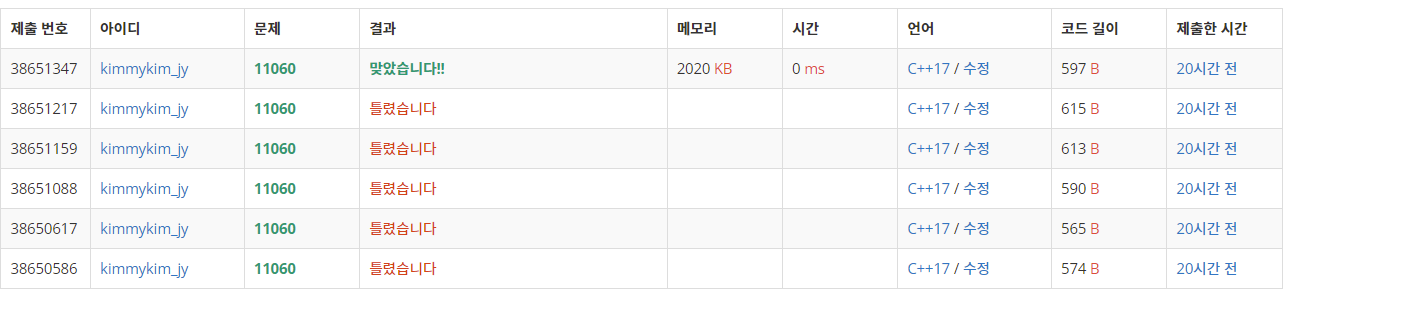
dp에서 이런 비슷한 유형의 문제를 풀어본 기억이 있어서 dp로 풀어야 겠다고 생각했다. 일단 int dp[]에서 dp[i]가 의미하는 것은 jump[i]에서 가장 오른쪽 끝으로 갈 수 있을 때까지 해야하는 최소 jump의 개수다. 그렇다면 마지막에 구해야 할 값은 dp[0]이다.

처음에 dp[]를 모두 무한대 값으로 초기화를 해두고 시작한다. 현재 위치를 cur이라고 두고 현재 위치 cur에서 점프할 수 있는 범위를 next라고 둔다.

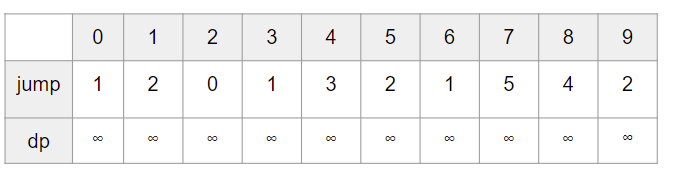
예를들어 위와같이 있을 때, dp[9]는 이미 끝에 도달해있으므로 jump[9]의 값과는 상관없이 1이다.
다음 dp[8]을 알아내고자 할 때, 현재 위치 cur=8이고, 점프할 수 있는 next의 범위는 1<=next<=4 이다.

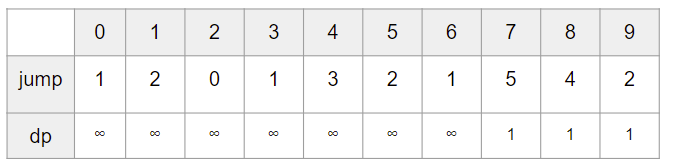
dp[7] 까지는 cur+next (next의 최댓값)이 9이상이므로 다 1이 된다.

	for (int cur= n-1; cur >= 0; cur--) {

		int x = jump[cur];
		for (int next = x; next > 0; next--) {
			if (cur + next >= n - 1) {
				dp[cur] = 1; continue;
			}
			else 
				다른 경우 처리
		}
	}

그 다음부터는 각 자리에서 점프해서 갈 수 있는 곳에 있는 dp[i]의 값에서 1을 더한 값과, 현재 자신의 dp[cur]을 비교해서 더 작은 값을 dp[cur]에 저장한다.

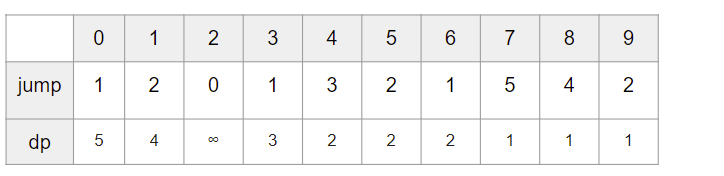
하다보면 이런 표가 완성된다.

문제를 풀다가 실수 2가지를 했는데

• N=1 이고 jump[0]=0 인 경우에는 이미 끝에 도달해 있으므로 1을 return 해야한다.
• 처음 dp를 무한대로 초기화 할 때, const int MAX=0xf7777777 로 초기화 했는데 이 값에 1을 더하는 경우가 생기므로 계속 -0xf7777777 로 바뀌고 있었다. 그래서 1e8로 초기화 했다.
  (또 다른 예로0x3f3f3f3f로 초기화 하면 두 배해도 int값은 안 벗어나면서 10억은 넘는 값이라서 max 설정할 때 많이 한다고 한다)

#include<iostream>
#include <vector>

const int INF = 1e8;
using namespace std;

int dp(vector<int> jump) {
	int n = jump.size();
	vector<int>dp(n, INF);
	if (n == 1) return 0;
	for (int cur= n-1; cur >= 0; cur--) {

		int x = jump[cur];
		for (int next = x; next > 0; next--) {
			if (cur + next >= n - 1) {
				dp[cur] = 1; continue;
			}
			else 
				dp[cur] = min(dp[cur], dp[cur + next] + 1);
		}
	}
	if (dp[0] == INF) return -1;
	else return dp[0];
}
int main() {
	int n;
	cin >> n;
	vector<int> jump(n);
	for (int i = 0; i < n; i++)
		cin >> jump[i];
	cout << dp(jump) << endl;
	return 0;
}