이진 탐색 트리

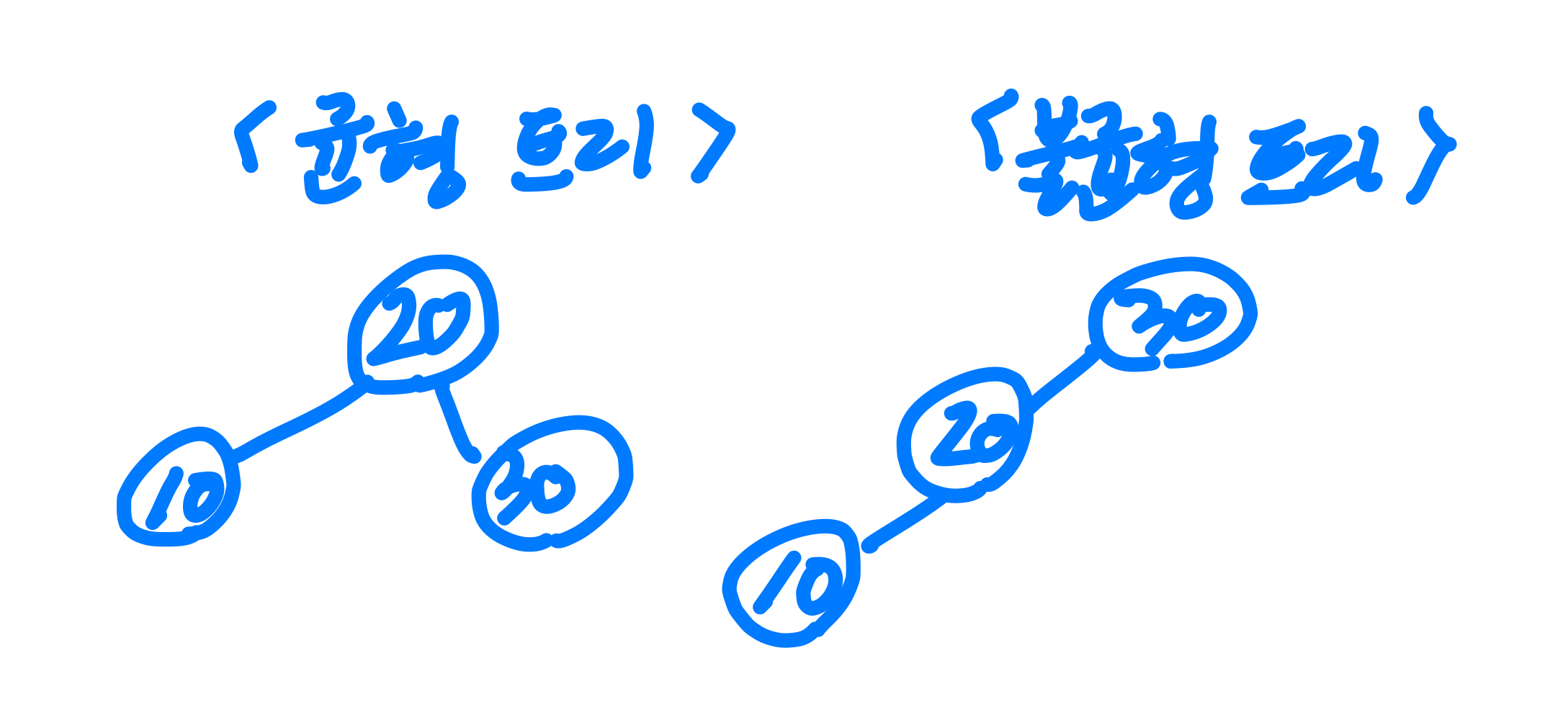
이진 탐색 트리(Binary Search Tree)란?

다음 규칙을 만족하는 트리

1. 각 노드의 자식이 2개 이하이다.
2. 왼쪽 자식 노드의 키는 부모 노드의 키보다 작다.
3. 오른쪽 자식 노드의 키는 부모 노드의 키보다 크다.
4. 각각의 서브 트리도 이진 탐색 트리를 유지한다.
5. 중복된 키를 허용하지 않는다.

중복이 없어야 하는 이유는?
검색 목적 자료구조인데, 굳이 중복이 많은 경우에 트리를 사용하여 검색 속도를 느리게 할 필요가 없음. (트리에 삽입하는 것보다, 노드에 count 값을 가지게 하여 처리하는 것이 훨씬 효율적)

이진탐색 트리의 목적?

• 이진탐색트리 = 이진탐색 + 연결리스트
• 이진탐색 : 탐색에 소요되는 시간복잡도 O(log N), 그러나 삽입/삭제 불가능
• 연결리스트: 삽입/삭제 시간복잡도 O(1), 그러나 탐색의 시간복잡도 O(N)
  -> 두가지의 점을 모두 얻는것이 이진탐색트리 : 효율적인 탐색능력과 자료의 삽입/삭제 가능!!

이진 탐색 트리의 특징

• 이진 탐색 트리 규칙에 의해 데이터가 정렬된다. => 중위순회로 탐색하면 오름차순으로 정렬된다.
• (균형을 유지하는 이진탐색트리라면) 이진트리에 비해 탐색이 빠르다.
  • 균형상태 : O(logN)
  • 불균형상태: O(N)
  • 삽입, 검색, 삭제 시간복잡도는 트리의 Depth에 비례
• 편향된 트리(정렬된 상태 값을 트리로 만들면 한쪽으로만 뻗음)는 시간복잡도가 O(N)이므로 트리를 사용할 이유가 사라짐 → 이를 바로 잡도록 도와주는 개선된 트리가 AVL Tree, RedBlack Tree
  

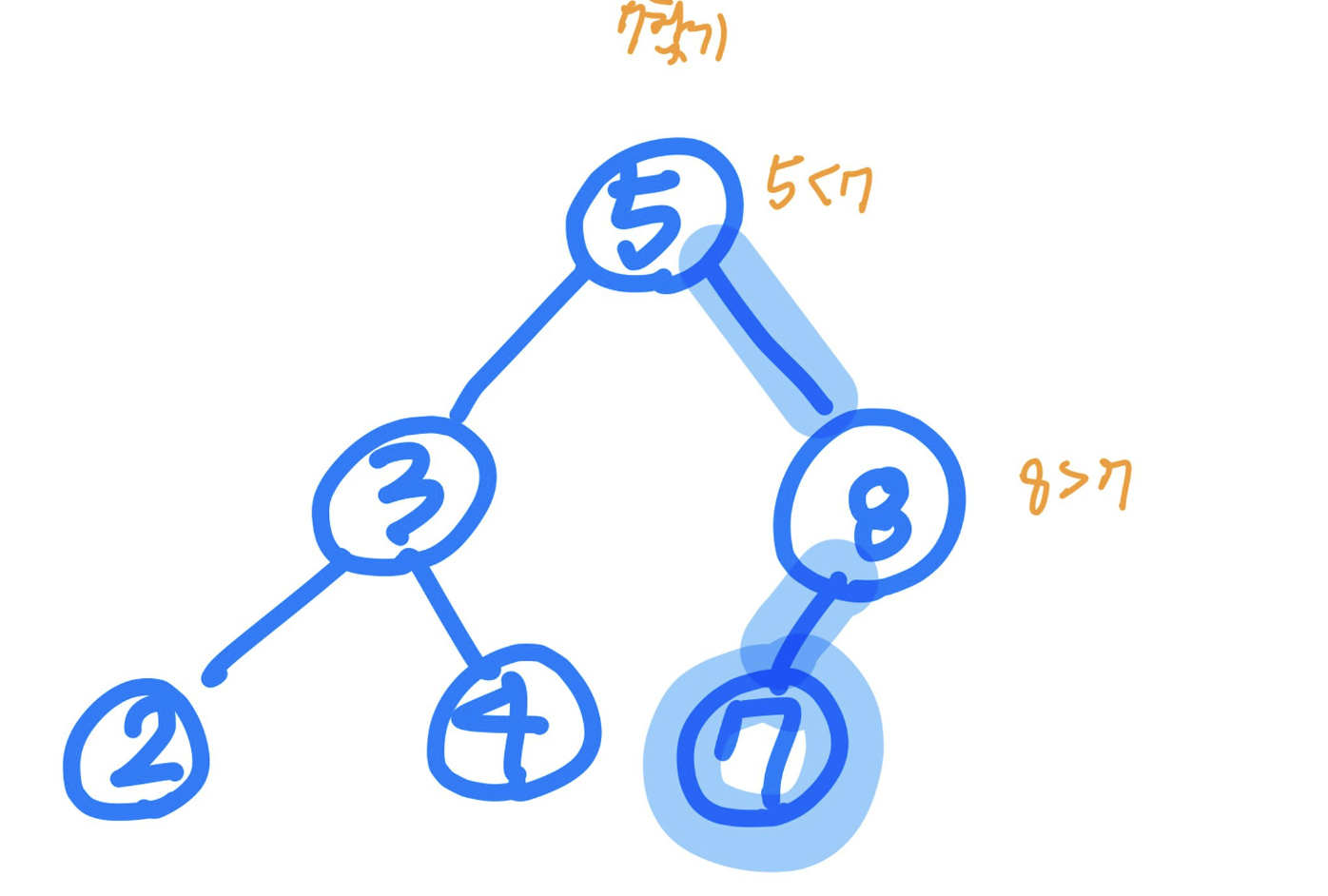
이진 탐색 트리 - 탐색

• 찾고자 하는 데이터를 루트노드부터 비교 시작
• 대소 비교를 통해 찾는 데이터가 작으면 왼쪽, 크면 오른쪽 노드로 이동
• 찾는 데이터가 없으면 null 반환
• 어떤 데이터를 찾더라도 최대 트리 높이 만큼의 탐색이 이루어짐
  

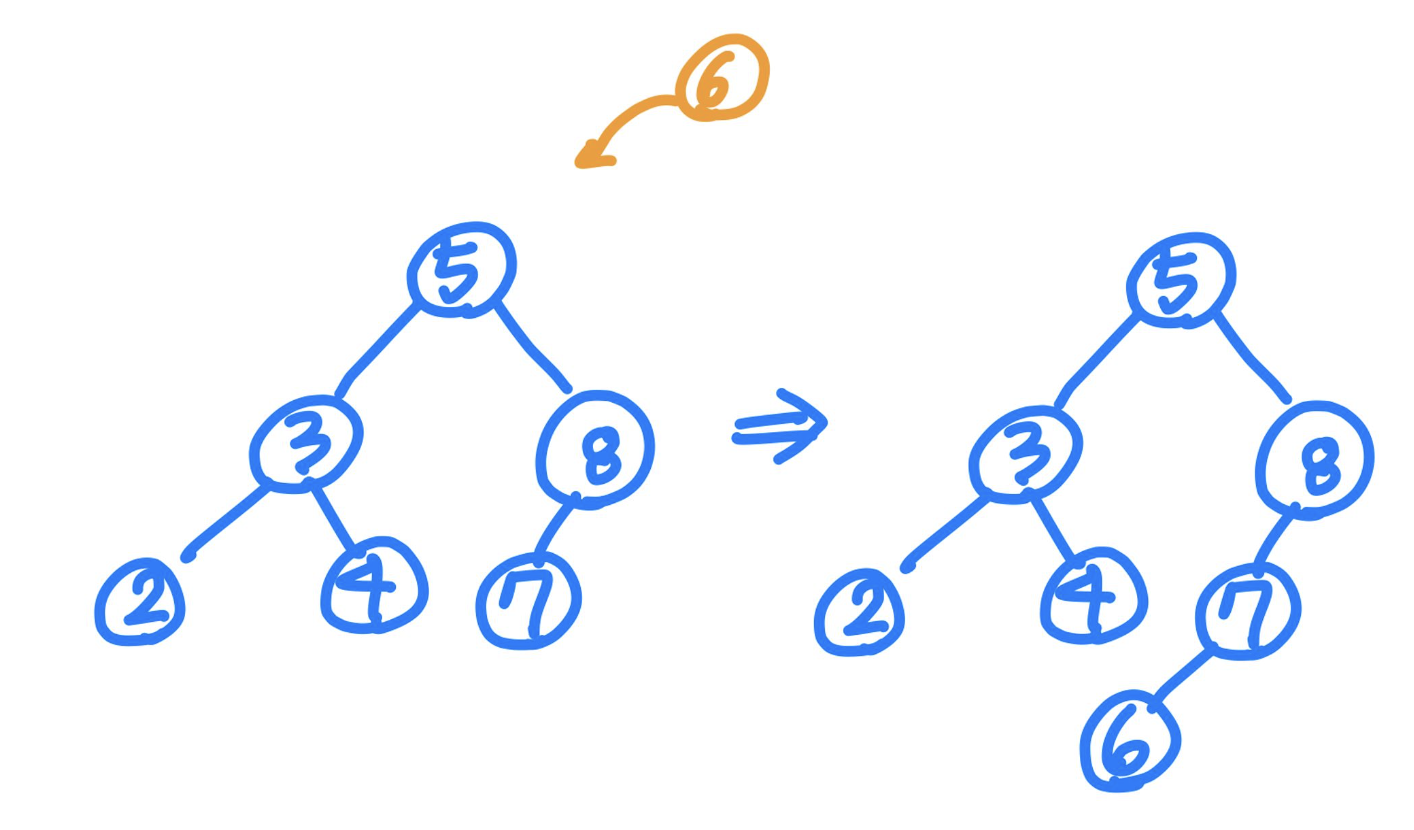
이진 탐색 트리 - 삽입

• 루트부터 비교 시작 (중복 키를 발견하면 노드 추가하지 않고 종료)
• 삽입할 키가 현재 노드의 키보다 작으면 왼쪽으로 이동
• 삽입할 키가 현재노드보다 크면 오른쪽으로 이동
• leaf노드에 도달한 후 비교하여 작으면 왼쪽, 크면 오른쪽에 삽입!

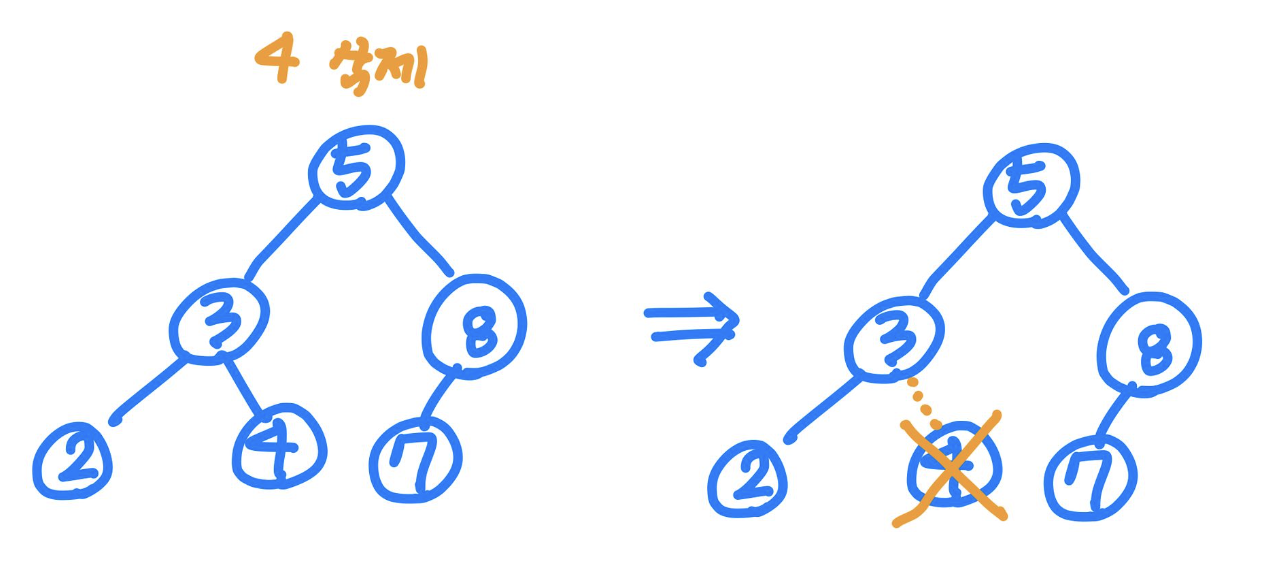
이진 탐색 트리 - 삭제 : 삭제 대상 노드가 leaf인 경우

• 삭제 대상 노드 삭제
• 부모노드의 해당 자식 링크 null로 변경
  

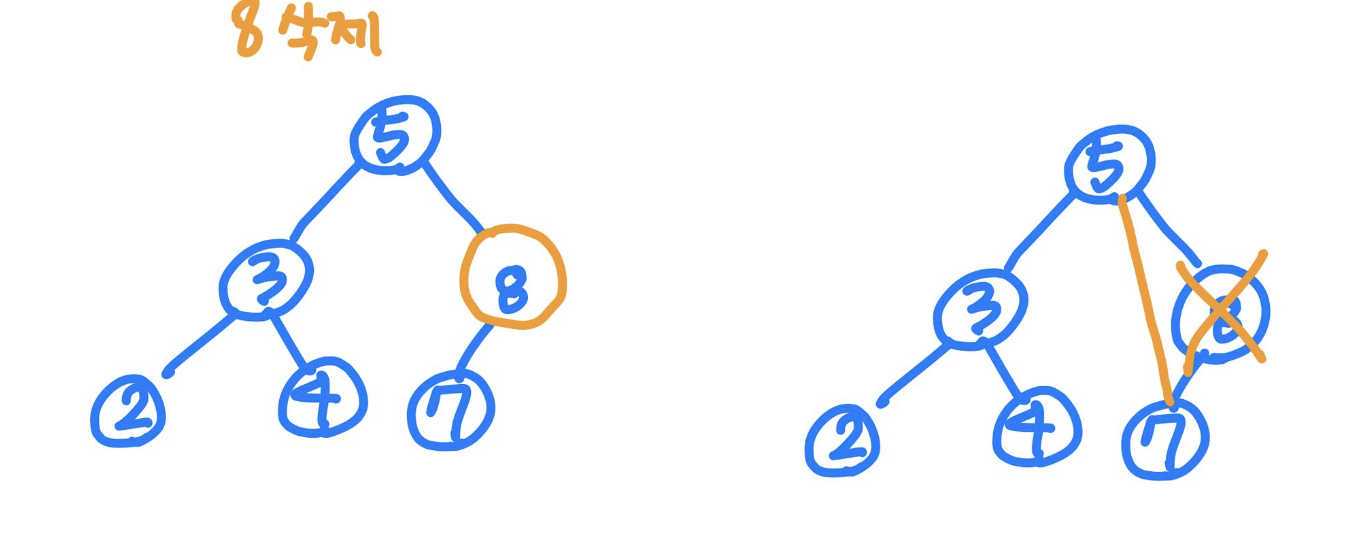
이진 탐색 트리 - 삭제 : 삭제 대상 노드에 자식 1개인 경우

• 삭제 대상노드의 자식 노드를 삭제 대상 노드의 부모노드에 연결
• 삭제 대상 노드 삭제

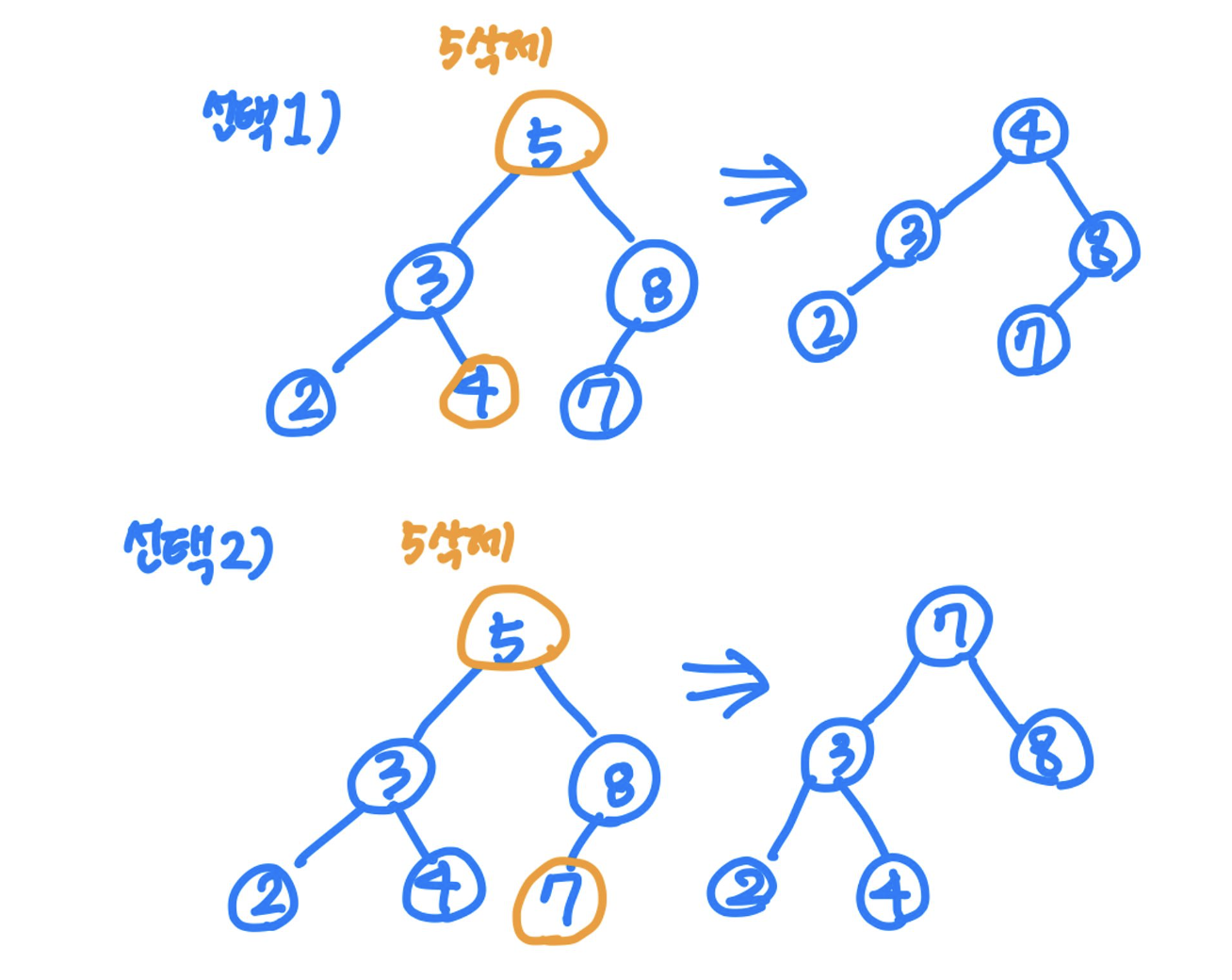
이진 탐색 트리 - 삭제 : 삭제 대상 노드에 자식 2개인 경우

1. 삭제 대상 노드의 왼쪽 서브트리에서 가장 큰 노드 선택
2. 삭제 대상 노드의 오른쪽 서브트리에서 가장 작은 노드 선택

• 1 또는 2에서 선택한 노드를 삭제 대상 노드 위치로 올림
• 위로 올리는 과정에서 다른 자식 노드들의 링크를 연결작업 진행
• 삭제 대상 노드 삭제