Logistic Regression
로지스틱리그레션은(Logistic Regression) 선형회귀(Linear Regression) 기반으로 하는 알고리즘으로 비슷하게 선형 관계를 기반으로 하는 알고리즘입니다. 다만 선형회귀 결괏값에 시그모이드함수를 취해줌으로써 분류(Classification)에 사용할 수 있습니다.
그만큼 유사하게 간결하고 효율적이라 베이스라인 모델로 많이들 사용됩니다.
특징은 선형회귀와 유사합니다.
- 분류 : Supervised learning
- 형태 : Linear Model
- 용도 : Regression
- 장점 : 간결함(베이스라인), 해석가능성(Interpretablilty), 효율성(Efficiency)
- 단점
- 피처간 낮은 상관관계(low-correlation)을 가정 (높은 independence)
- 너무 간단한 형태의 모형으로 underfitting의 위험성
- 아웃라이어(outlier)에 취약
1. Model
Logistic Regression의 모델은 Linear Regression과 마찬가지로 데이터 feature들의 선형결합으로 이루어지지만, 연산의 결과가 0과 1의 두 경우에 한정되도록 하기위해 시그모이드(sigmoid)함수에 취하게 됩니다. 시그모이드는 다음과 같이 사이의 공역을 지니는 함수이며 시그모이드 함수에 대한 자세한 설명은 다음에 다른 포스트에서 다루도록 하겠습니다.
# How Sigmoid Looks
import matplotlib.pyplot as plt
import numpy as np
def sigmoid(x):
return 1/( 1 + np.exp(-x))
x = np.linspace(-10, 10, 100)
y = sigmoid(x)
plt.plot(x, y)
plt.title('Sigmoid')
plt.xlabel('x')
plt.ylabel('sigmoid(x)')
plt.grid(True)
plt.show()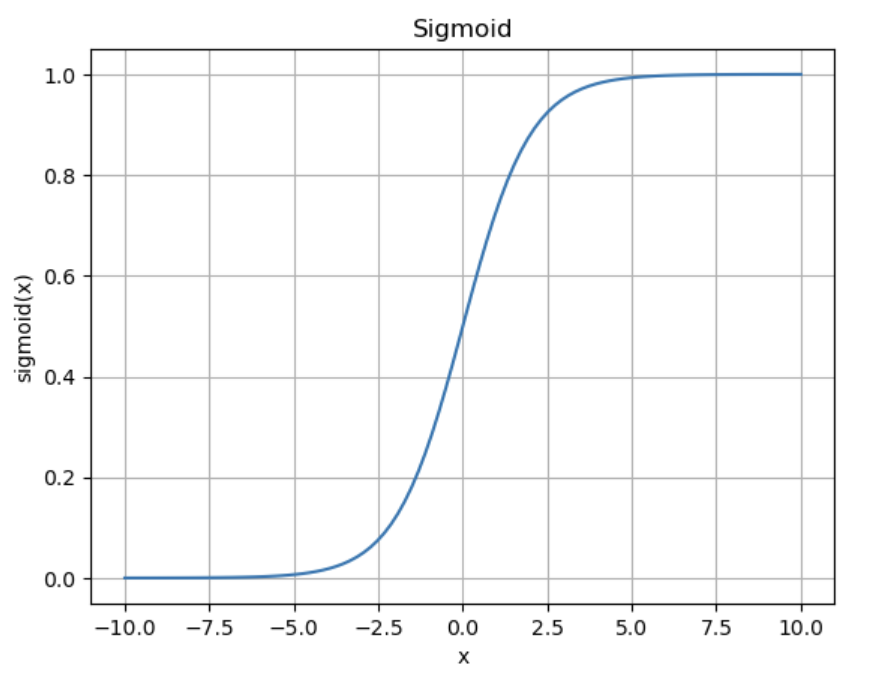
Feature간의 선형결합 수식에 시그모이드 함수를 취하면 다음과 같은 Rogistic Regression 모델의 수식을 얻을 수 있습니다.
2. Objective Function
Linear Regression에서는 MSE(Mean Square Error)을 통해서 오차의 제곱함을 최소화하는 목적함수를 정의했었다면, Logistic Regression에서는 최대우도법(Maximum Likelihood Estimation)을 통해 관측 값(데이터 샘플)이 가장 가깝게 근사하는 분포를 찾는 것을 목적함수로 합니다.
Maximum Likelihood Estimation에 대해서는 다른 포스트에서 다시 다루기로 하고 여기서는 수식만 간단하게만 짚고 넘어가도록 하겠습니다.
어떠한 데이터 샘플 의 각 데이터 요소들을 라 하고 이러한 샘플 데이터를 대표하는 가장 적절한 모집단 분포(확률분포)를 표현하는 벡터 를 알고자 할때, 각 샘플의 likelihood 값() 의 곱을 최대로 하는 를 구하는 것이 Maximum Likelihood Estimation입니다. (각 샘플은 독립사건이라고 가정)
그럼 다시 돌아와서 Logistic Regression을 살펴보자면, 특정 관측값()의 Logistic Regression의 모델 의 결과는 0~1 사이의 확률 값()으로 떨어지게 되는데 사실상 binary classification에서 결과는 0과 1 두가지 밖에 존재할 수 없으므로 확률분포는 베르누이 분포의 형태를 띄게 됩니다.
즉, 실제 결과 가 1일때 확률 값()은 이 될 것이고 가 0일때의 확률 값()은 가 될 것인데, 이를 수식으로 정리하면 다음과 같습니다.
이를 하나의 수식으로 요약하면 다음과 같이 표현할 수 있고 이것이 binary logistic regression의 확률질량함수(pmf)가 됩니다.
자, 그럼 이제 이를 최대우도법의 형태로 표현하자면 각 샘플(row)의 확률 값을 전부 곱하였을때의 결과가 최대가 되게 하는 와 을 구하는 것이 목표가 되고 아래 식이 목적함수가 됩니다.
여기서 계산의 편의를 위해 양측에 로그를 취하도록 하겠습니다. 어차피 로그함수는 단조증가함수이기때문에 결과가 최대로 나오게하는 와 는 변하지 않기 때문입니다. 그리고 이를 log-likelihood라 부릅니다. 양 변에 자연로그를 취하면 다음과 같은 형태로 표현할 수 있습니다.
이제 이러한 log-likelihood 함수를 최대화 하는 와 를 찾으면 되는데, 대부분의 optimization 방법론이 결과를 최소화하는 방식으로 설계되어 있으므로 다음과 같이 앞에 -를 붙여 Negative Log-Likelihood(NLL)을 사용하곤 합니다.
3. Optimization
그럼 목적함수를 정의하였으므로 이를 최소화할 수 있는 변수 와 를 찾으면 됩니다. 이를 위해서는 Linear Regression과 마찬가지로 경사하강법(Gradient descent)을 사용하겠습니다. 그 이유는 목적함수가 convex한 형태이기 때문에 경사하강법으로 최소값을 찾을 수 있습니다.
목적함수를 간단하게 1차 피처를 기준으로 그려보면 다음과 같이 global minimum이 존재하는 것을 확인할 수 있습니다.
import numpy as np
import matplotlib.pyplot as plt
# Define the objective function (negative log-likelihood) for logistic regression
def objective_function(theta, x, y):
# Compute the predicted probabilities
z = np.dot(x, theta)
p = 1 / (1 + np.exp(-z))
# Compute the negative log-likelihood
nll = -np.sum(y * np.log(p) + (1 - y) * np.log(1 - p))
# Return the objective function value
return nll
# Generate some sample data
x = np.array([1, 2, 3, 4, 5])
y = np.array([0, 0, 1, 1, 1])
# Define a range of values for theta
theta_range = np.linspace(-30, 30, 100)
# Compute the objective function for each value of theta
objective_values = np.zeros_like(theta_range)
for i in range(len(theta_range)):
theta = np.array(theta_range[i])
objective_values[i] = objective_function(theta, x, y)
# Plot the objective function
plt.plot(theta_range, objective_values)
plt.xlabel('theta')
plt.ylabel('Negative Log-Likelihood (NLL)')
plt.title('Objective Function')
plt.grid(True)
plt.show()
