3. 힙
힙이란, 힙의 특성(최대 힙에서는 부모 노드의 데이터가 항상 자식 노드의 데이터보다 크다)을 만족하는 거의 완전한 트리인 특수한 트리 기반의 자료구조이며, 주로 우선순위 큐를 구현할 수 있다. 거의 완전한 트리에 대해서는 있다가 이진 완전 트리와의 비교를 통해 개념을 정리할 예정.
원래 파이썬의 기본 힙 구조는 최소 힙이 디폴트이며, 최대 힙은 별도로 제공되지 않는다. 그렇지만 처음 힙을 공부할 때 접한 개념이 최대 힙이고 최소 힙의 각 노드의 데이터를 음수배한 것이 최대 힙(파이썬에서도 똑같이 구현된다)이므로 최대 힙을 기준으로 끄적끄적.
1) 힙의 개념
(1) 이진 힙과 이진 탐색 트리
둘은 형태가 상당히 유사하지만, 근본적인 차이점으로 이진 힙은 데이터의 상하 관계를 보장한다. 반대로 이진 탐색 트리는 데이터의 좌우 관계를 보장한다.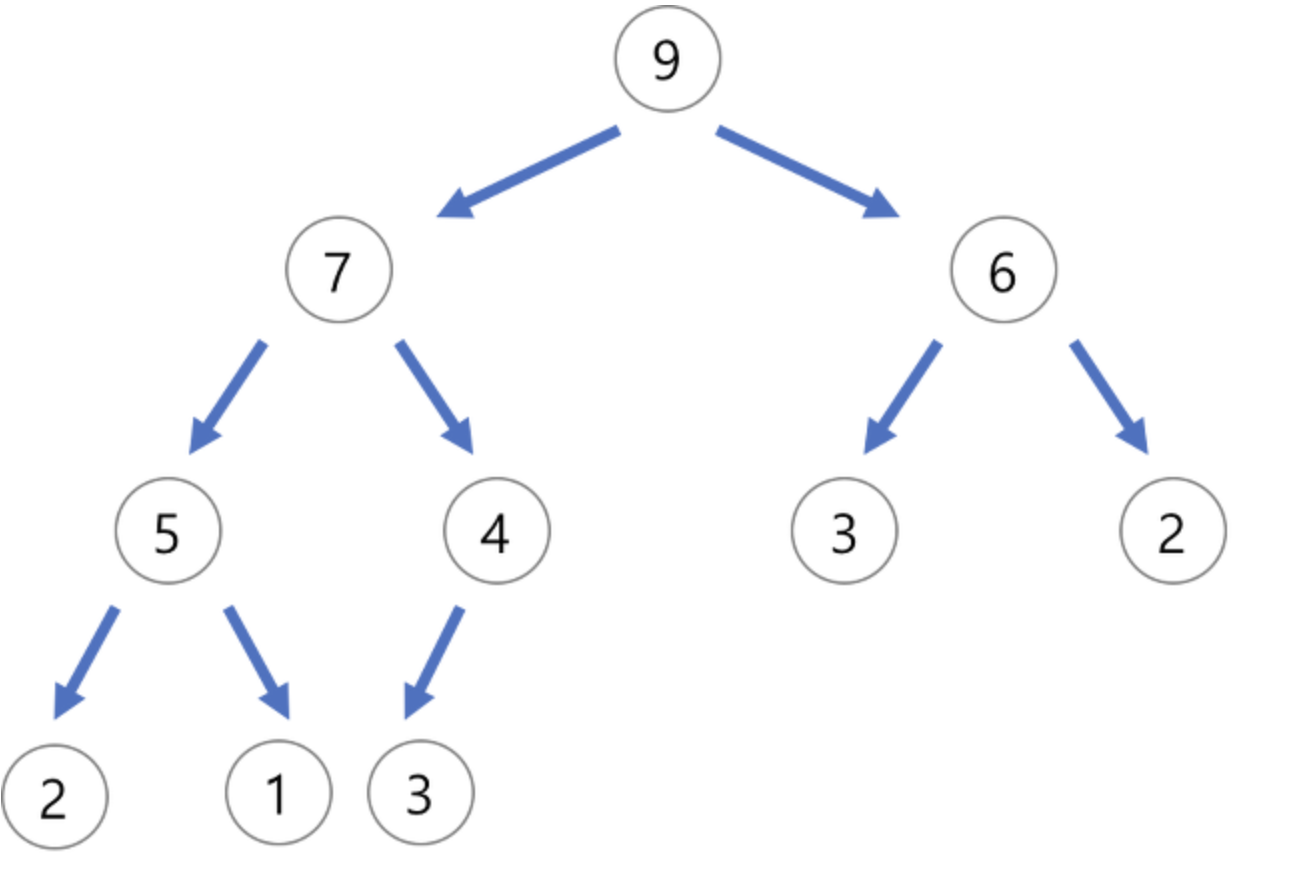 위의 그림은 이진 힙(정확히는 최대 힙)이다. 부모 노드의 데이터가 자식 노드의 데이터보다 언제나 크거나 같으며, 이 특성 덕분에 중복 데이터의 삽입이 가능하다. 또한, 힙은 맨 아래 자식 노드들을 제외하고 왼쪽 자식 노드가 오른쪽 자식 노드보다 작거나 같게 된다.
위의 그림은 이진 힙(정확히는 최대 힙)이다. 부모 노드의 데이터가 자식 노드의 데이터보다 언제나 크거나 같으며, 이 특성 덕분에 중복 데이터의 삽입이 가능하다. 또한, 힙은 맨 아래 자식 노드들을 제외하고 왼쪽 자식 노드가 오른쪽 자식 노드보다 작거나 같게 된다.
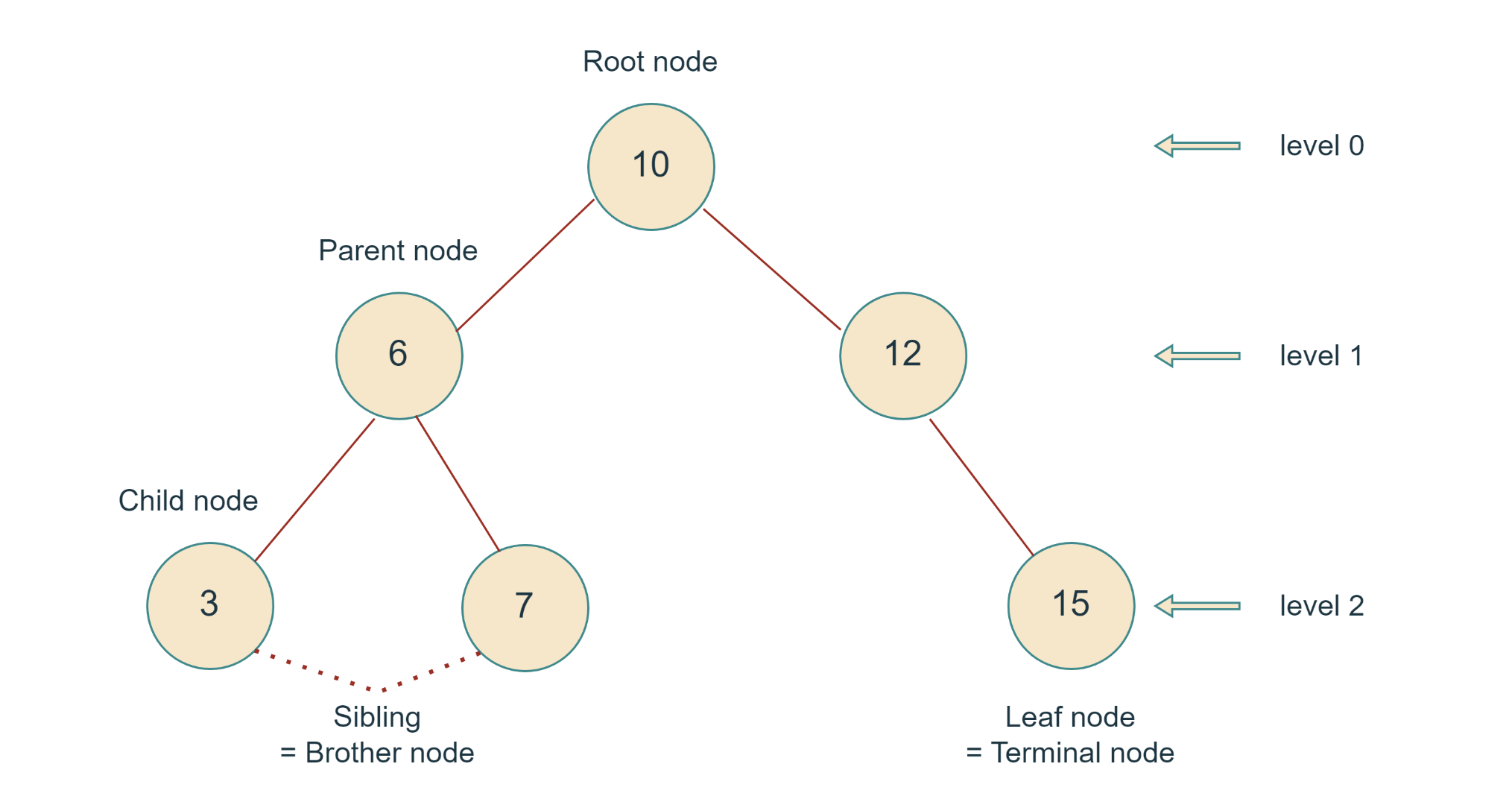 위의 그림은 이진 탐색 트리다. 노드들 간의 관계에 있어서 중요하게 볼 것은, 동일 부모를 지니는 형제 자식 노드들끼리 이루는 관계다. 언제나 왼쪽 자식 > 부모 > 오른쪽 자식 관계의 데이터를 배치받게 되며 중복 데이터가 허용되지 않는다.
위의 그림은 이진 탐색 트리다. 노드들 간의 관계에 있어서 중요하게 볼 것은, 동일 부모를 지니는 형제 자식 노드들끼리 이루는 관계다. 언제나 왼쪽 자식 > 부모 > 오른쪽 자식 관계의 데이터를 배치받게 되며 중복 데이터가 허용되지 않는다.
용도에 따라 정리하자면, 이진 힙은 최대, 최소값 산출, 이진 탐색 트리는 데이터 탐색에 특화된 형태다.
참조 링크
https://chunsubyeong.tistory.com/88
https://www.baeldung.com/cs/heap-vs-binary-search-tree
(2) 힙의 시간복잡도
- 삽입(Insertion):
O(log n)- 삭제(Deletion):
O(log n)- 최소/최대값 검색(Find minimum/maximum):
O(1)
(3) 파이썬에서의 힙
파이썬에서 최대, 최소값을 구하기 위해 제공하는 힙 자료구조는 heapq 모듈을 통해 활용할 수 있다. 파이썬에서의 힙은 최소 힙이 디폴트며, 최대 힙이 별도로 제공되지 않는다. 대신 요소의 음수배를 통해 최대 힙을 간접적으로 구현하고 최대값 산출 역시 가능해진다.
import heapq
# 임시 리스트
heap = [3, 1, 4, 1, 5, 9, 2, 6]
# 리스트를 힙으로 변환
# 언급했듯, 파이썬의 힙은 최소 힙이 디폴트
heapq.heapify(heap)
print(heap) # [1, 1, 2, 6, 5, 9, 4, 3]
# 최소 힙에 원소 추가
heapq.heappush(heap, 7)
print(heap) # [1, 1, 2, 6, 5, 9, 4, 3, 7]
# 최소 힙에서 최소값 산출
min_element = heapq.heappop(heap)
print(min_element) # 1
print(heap) # [1, 3, 2, 6, 5, 9, 4, 7]
# 최소 힙에서 가장 작은 원소를 제거하고 새로운 원소 추가
min_element = heapq.heapreplace(heap, 8)
print(min_element) # 1
print(heap) # [2, 3, 4, 6, 5, 9, 8, 7]최대 힙을 세팅하는 방법은 heapify() 메소드를 통해 힙으로 변환하는 과정에서 순차적으로 입력되는 요소들을 음수배하는 것이다.
import heapq
# 최대 힙으로 사용할 리스트
max_heap = []
# 데이터 삽입 (음수로 변환하여 최소 힙에 삽입)
heapq.heappush(max_heap, -3)
heapq.heappush(max_heap, -1)
heapq.heappush(max_heap, -4)
heapq.heappush(max_heap, -1)
heapq.heappush(max_heap, -5)
# 최대 힙에서 가장 큰 값 추출 (음수로 변환된 가장 작은 값)
max_value = -heapq.heappop(max_heap)
print(max_value) # 52) 힙의 매커니즘
앞서 말했듯이 힙은 최대값 혹은 최소값을 뽑아내는 것에 특화된 자료구조이기 때문에 산출은 빠르게 이뤄지고, 내부의 조정 과정이 이뤄져야 할 것이다. 대략적인 의사코드를 통해 매커니즘을 정리, 이해하자.
아래의 의사코드는 전부 알고리즘을 같이 공부하는 박 군의 힙 커스터마이징으로부터 차용됐으며, 이를 허락해준 박 군에게 감사의 인사를 액션빔✨
해당 당사자의 깃헙 링크
https://github.com/qkrckstjq
추후에 2회독, 혹은 시간 여유가 생기면 힙 커스터마이징 예정 업데이트
(1) 초기화
우선 최대 이진 힙을 구현하기 위해서 리스트를 사용하며, 각 노드의 위치는 리스트의 인덱스로 배정한다. 여기서 중요한 점은 리스트의 0번째 인덱스는 사용하지 않고, 루트 노드의 인덱스는 1로 배치하면서 순차적으로 자손 노드들의 인덱스를 부여할 수 있게 한다.
# 리스트를 선언하며, 인덱스 0은 사용하지 않도록 None을 산입한다.
초기화 된 리스트 = [None](2) 데이터 산입
리스트에 데이터를 산입하면서 중요한 것은 해당 데이터를 어떤 인덱스에 부여할 것인지와 기존의 인덱스에 이미 자리를 잡은 다른 데이터 노드들과 어떻게 재배치할 것인지에 대한 해결책이다.
힙의 단위 이진 트리에서 부모 노드의 인덱스(n)를 기준으로 왼쪽 자식의 노드는 2n의 인덱스를 부여하고, 오른쪽 자식의 노드는 2n + 1의 인덱스를 부여한다. 이 과정을 재귀적으로 반복하면서 지속적으로 입력되는 데이터의 인덱스를 배치시킨다.
# 부모 노드 인덱스 : n
# 왼쪽 자식 노드 인덱스 : 2n
# 오른쪽 자식 노드 인덱스 : 2n + 1
[ ... index n, ..., index 2*n, index 2*n+1 ... ]
# 반대로 말하면
# 자식 노드의 인덱스 // 2 = 직속 부모 노드의 인덱스새로운 데이터는 항상 맨 마지막의 인덱스에 산입된다. 산입 후의 별도 상향 조정 과정을 통해 힙 구조를 유지하게 된다. 이 과정을 재배치(heapify)라고 칭한다.
분류 과정은 현재 본인 위치를 기점으로, 자신의 부모 인덱스에 위치한 노드 데이터 값을 얻어와 비교한다. 최대 힙의 경우, 부모 노드의 데이터가 자식 노드의 데이터보다 커야 되므로 서로를 스왑(swap)해야 한다. 여기서 형제 노드를 고려할 필요는 없다. 어차피 부모 노드가 다른 형제 노드의 데이터 값보다 크거나 같을 것이 자명하기 때문이다.
# 자신의 인덱스가 1일 때까지
# 그리고 직속 부모 노드 데이터 > 현재 자신의 데이터
while 조건:
부모의 데이터와 비교해서 크기가 크면 스왑(2) 최대 데이터 추출
최대 데이터 추출은 곧 인덱스 1에 위치한 데이터를 검색, 추출만 하면 된다. 다만 추출 이후의 이진 구조를 유지시키기 위한 재배치 작업이 필요하다.
이를 위해서 우선 현재 리스트에서 가장 마지막 인덱스의 데이터를 루트 노드로 갖고 오는 작업으로 시작하게 된다. 그런 다음, 루트 노드로부터 자식 노드의 데이터들과 비교하면서 스왑하는 과정으로 하향 재배치가 이뤄진다.
# 인덱스 1의 데이터가 최대값
최대값 데이터 = 리스트[1]
# 재배치 작업을 위한 마지막 인덱스와 최대값의 인덱스를 스왑
리스트[1] = 리스트[-1]
# 마지막 인덱스로 보내진 최대값을 pop하며 리스트에서 없앤다.
리스트.pop()리스트에서 스왑된 최대값을 pop함으로써 해당 데이터를 리스트에서 배제하고 이진 구조 유지를 위해 현재 인덱스 1에 위치한 데이터 노드를 직속 자식 노드들과 비교하면서 하향 재배치를 수행한다.
그 전에, 잠시 자식 노드들의 인덱스 배치에 대해 고찰하자면 현재 해당 과정은 모든 자연수를 도출하기 위한 간단한 수식을 사용하고 있다. 그리고 이진 트리의 구조를 지니므로 아마 이런 식으로 도식화가 가능할 것이다.
2^1
2^2 2^3
2^4 2^5 2^6 2^8
# ...이진 구조이기 때문에 레벨에 따라 2의 n제곱 만큼의 노드 개수를 지니게 되며 그 배치는 위에서 언급했던 왼쪽 자식의 인덱스(2n)와 오른쪽 자식의 인덱스(2n + 1)를 부여하게 된다. 즉, 입력 데이터의 인덱스 배치는 왼쪽 자식이 우선이라는 것이다.
그렇기 때문에 하향 재배치에 있어서는 왼쪽 자식을 우선으로 잡되, 오른쪽 자식과의 데이터 비교 역시 포함시키며 하향의 방향을 조정하는 것이 재배치의 핵심 로직이다. 물론 이것은 필수적인 것은 아니고 수많은 구현 과정 중 일부일 것이다.
# 왼쪽 자식 값이 리스트의 마지막 인덱스에 닿을 때까지
while 조건:
# 부가 조건 : 인덱스가 리스트 범위 내인지
왼쪽 자식과 오른쪽 자식을 비교해서 스왑 대상 정하기
if 현재 데이터 >= 자식 데이터:
break
# 다음 반복을 위한 변수 업데이트