O(n)의 등장

이때까지 봐온 모든 정렬 알고리즘들은 입력된 숫자들을 비교해가며 정렬을 하였다. 하지만 비교하며 정렬하는 모든 알고리즘은 O(n log n)이라는 명확한 한계를 가지고 있다. 그렇다면 어떻게하면 정렬 알고리즘을 더욱 빠르게 작동시킬 수 있을까? 바로 비교를 하지 않으면 된다. O(n) 시간에 실행되는 정렬 알고리즘들은 비교를 하지 않고 정렬을 한다는 특징을 가지고 있다.

계수 정렬

계수 정렬은 말 그대로 x에 대해서 x보다 같거나 작은 원소의 개수를 센다. 이렇게 센 값은 나중에 x를 어디에 배치할 것인가를 결정할 때에 사용된다.

예를 들어 [2, 1, 3, 4, 8, 7, 9] 라는 배열이 있다고 가정해보자 이때 x에 대해서 같거나 작은 원소의 개수를 센다면

0 = 0
1 = 1
2 = 2
3 = 3
4 = 4
7 = 5
8 = 6
9 = 7

이 된다. 이제 다른 배열을 하나 더 만들어서 오른쪽에 있는 값을 인덱스로 하여 왼쪽에 있는 값을 넣어주면 다음과 같이 정렬된 배열이 만들어진다.

[1, 2, 3, 4, 7, 8, 9]

계수 정렬의 장점

계수 정렬의 장점은 당연히 속도다. O(n) 으로 지금까지 봤던 어떤 정렬 알고리즘보다 빠르고 간단하게 정렬한다. 또한 계수 정렬은 안정성을 가지는데 안정성은 출력되는 배열에서 값이 같은 숫자가 입력되는 배열에 있던 것과 동일한 순서로 출력된다는 것을 의미한다. 보통 이 안정성이 중요하게 여겨질 때는 정렬되는 원소에 부속 데이터(Ex: 문서, JSON 등)가 붙어다닐 때이다. 또한 다음 포스트에서 설명할 기수 정렬이 정확하게 작동하기 위해서도 계수 정렬의 이 안정성이 중요하다.

계수 정렬의 단점

계수 정렬은 빠르고 간단한 좋은 알고리즘이지만 이 알고리즘의 발목을 잡는 제약이 있다. 바로 입력되는 배열이 0 부터 k 사이의 정수라는 가정하에 정렬을 시작한다는 점이다. 이를 위해서는 배열에서 가장 큰 값이 무엇인지 알아야만 하는데 이를 알지 못한다면 계수 정렬을 사용할 수 없다.

코드

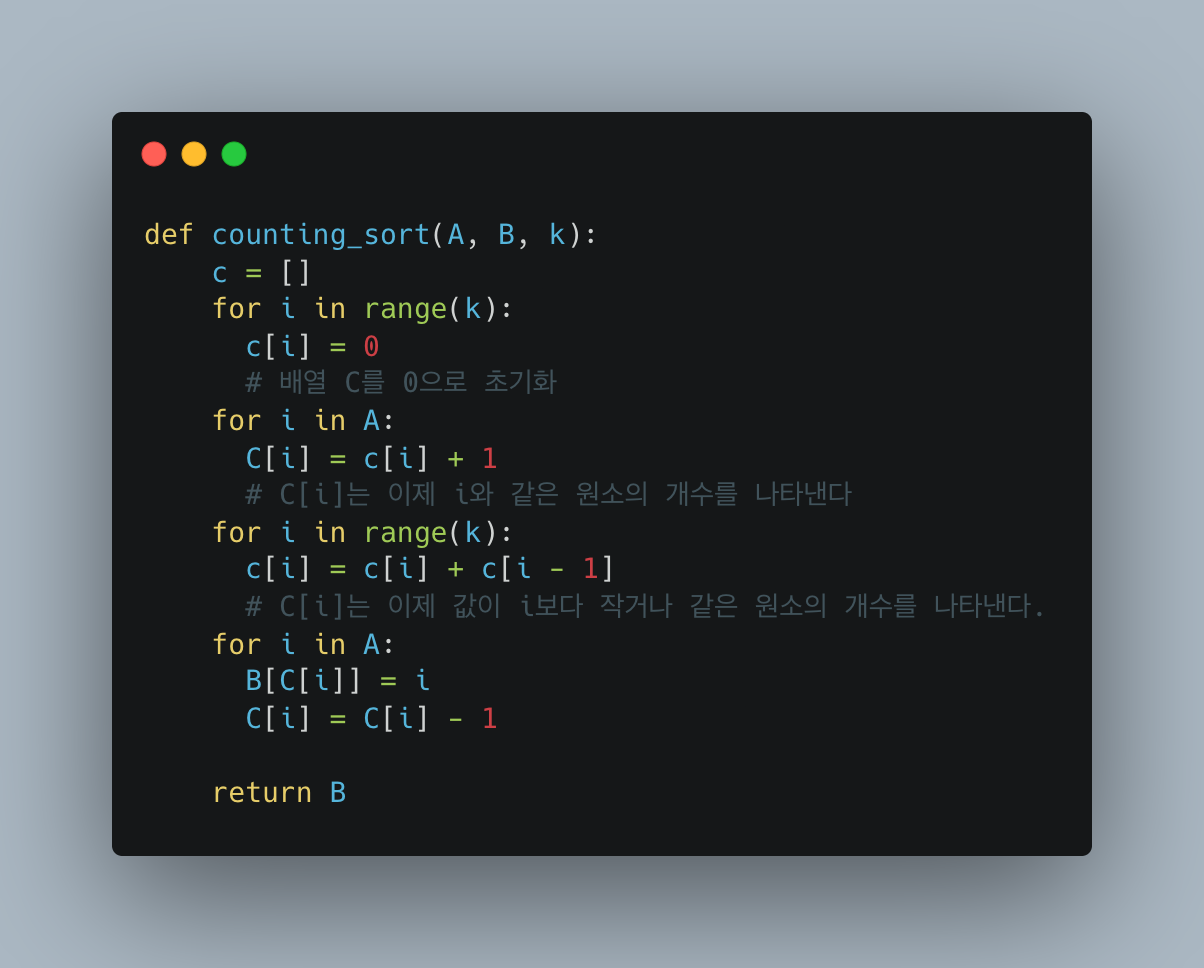
위의 코드는 배열 A에 대하여 계수 정렬을 실행한다.

수행시간

위에서 말했다시피 계수 정렬은 O(n)의 시간이 걸린다. 먼저 2-3행의 for 루프는 O(k) 시간, 7-8행의 for 루프는 O(k) 시간, 10-12행의 for 루프는 O(n) 시간이 걸린다. 따라서 총 시간은 O(k + n)이 된다. 보통의 경우는 k = O(n) 일 때 계수 정렬을 사용하고, 이 경우 수행시간은 O(n)이 된다.

결론

비교 정렬의 한계 O(n log n) 을 뛰어넘어 O(n) 이라는 경이로운 수행 시간을 달성한 컴퓨터 공학자들이 정말로 대단하다고 생각한다. 계수 정렬은 간단하고 빠른 알고리즘이다만 확실히