안녕하세요!
이번 포스팅에서는 백트래킹 알고리즘 기법과 그래프 자료구조에 대해서 정리해보겠습니다.
Backtracking
알고리즘을 풀 때, 모든 조합을 시도해서 문제의 해를 찾아내는 방법은 해를 얻을 때까지 모든 가능성을 시도합니다.
위의 알고리즘 기법은 보통 재귀 함수로 구현되며 완전 탐색의 대표적인 방법은 BFS, DFS가 있습니다.
하지만 위의 방법을 사용하면 해답이 될 가능성이 전혀 없는 조합까지도 모두 시도해봐야하기 때문에 비효율적 입니다.
재귀 함수가 시간적으로 효율적인 함수가 아닌데다가, 호출 횟수가 시간 복잡도가 되기 때문에 재귀 함수에서 시간적인 효율성을 높이려면 함수 호출 횟수를 줄이는 것이 관건입니다.
백트래킹 알고리즘 기법은 어떤 노드의 유망성을 점검한 후에 유망하지 않다고 결정되면 그 노드의 부모로 되돌아가 다음 자식 노드로 가는 방법입니다.
- 유망하다
promising
어떤 노드를 방문했을 때 그 노드를 포함한 경로가 해답이 될 수 있으면 유망하다고 한다. - 가지치기
pruning
유망하지 않은 노드가 포함되는 경로는 더 이상 고려하지 않는다. - 백트래킹
backtraking
유망하지 않은 노드의 부모로 되돌아간다.
백트래킹의 과정
- 상태 공간 트리의 깊이 우선 검색을 실시한다.
- 상태 공간 트리 : 문제 해결 과정 중간 상태를 트리로 나타낸 것
- 각 노드가 유망한지 점검한다.
- 유망하지 않다면, 그 노드의 부모 노드로 돌아가 검색을 계속한다.
- 유망하다면 검색을 계속한다.
N-Queens 문제
NxN 체스판에서 N개의 Queen 을 배치하는데 이 Queen 들이 서로 위협하지 않도록 N개의 Queen 을 배치하는 문제입니다.
Queen 은 같은 열, 같은 행, 대각선 상에 위치하면 해당 Queen 은 위협받는 것입니다.
이 N개의 Queen 을 배치하는 조합을 완전 탐색으로도 구현할 수 있지만, 시간 초과가 발생하는 문제들이 다수입니다.
이 문제를 백트래킹으로 구현한다면 시간적인 효율성을 가져갈 수 있을 것입니다.
N-Queens 구현 코드
int[] queens = new int[N+1];
void nqueens(int rowNum) {
if (rowNum > N) {
System.out.println(Arrays.toString(queens));
return;
}
for (int i = 1; i <= N; ++i) {
queens[rowNum] = i;
if (isPromising(rowNum)) nqueens(rowNum+1);
}
}
boolean isPromising(int rowNum) {
for (int k = 1; k < rowNum; ++k) {
if (queens[k] == queens[rowNum] ||
Math.abs(queens[rowNum]-queens[k]) == rowNum-k) {
return false;
}
}
return true;
}Java 언어를 사용한 간단한 코드로 구현한다면 위와 같아질 것입니다.
퀸의 제약조건 중에서 같은 행, 같은 열, 대각선에 있으면 안되기 때문에 무조건 다른 행에 N개의 퀸을 놓는다는 전제 하에 queens 배열을 1차원 배열로 선언해 해당 열에 퀸을 배치하는 것이 유망한지 체크합니다.
(N+1 로 선언한 것은 퀸을 1열부터 배치한다고 가정했기 때문입니다.)
nqueens 메소드를 처음 실행할 때는 매개변수로 1을 넣을 것입니다.
1행의 퀸을 먼저 놓고, 그 다음 행의 퀸을 넣는 순서대로 실행될 것이기 때문입니다.
nqueens 메소드의 기저 조건은 rowNum 이 N 보다 커질 때입니다.
rowNum 이 N+1 이라면 모든 퀸을 배치한 것이므로 배치된 퀸을 출력하고 return 합니다.
퀸이 모두 배치되지 않았다면 for 문을 1열부터 N열까지 반복하며 퀸을 놓을 수 있는지 확인합니다.
반복문에서 우선 해당 행의 queens 배열에 i열을 대입하고 해당 열에 퀸을 배치하는 것이 유망한지 isPromising 메소드로 확인합니다.
만약 유망하다면 해당 열에 퀸을 배치하고, 유망하지 않다면 계속 반복문을 돌면서 유망한 열을 찾아서 퀸을 배치합니다.
유망한지의 여부는 1행부터(1번 인덱스부터) 해당 행까지 queens 배열의 요소들을 확인합니다.
queens[k] == queens[rowNum] 이 해당된다면 같은 열 에 퀸을 놓은 것이므로 유망하지 않습니다.
rowNum-k == Math.abs(queens[k]-queens[rowNum]) 이 해당된다면 대각선상 에서 일치하는 것이므로 유망하지 않습니다.
그래프
그래프는 N:M 의 관계를 갖으며 정점들의 집합과 이들을 연결하는 간선들의 집합으로 구성된 자료구조입니다.
선형 자료구조나 트리 자료구조로 표현하기 어려운 다대다 관계의 원소들을 표현하기 용이합니다.
- 정점 (
Vertex) : 그래프의 구성요소로 하나의 연결점 - 간선 (
Edge) : 두 정점을 연결하는 선 - 차수 (
Degree) : 정점에 연결된 간선의 수
그래프의 유형
- 무향 그래프 (
Undirected Graph)
방향이 없는 그래프를 뜻하며, 양방향의 특성을 지닌다. - 유향 그래프 (
Directed Graph)
방향이 있는 그래프를 뜻하며, 단방향의 특성을 지닌다. - 가중치 그래프 (
Weighted Graph)
정점들 사이의 간선이 가중치를 갖는 그래프를 말한다. - 사이클 없는 방향 그래프 (
DAG, Directed Acyclic Graph)
방향 그래프들 중에서 사이클이 나타나지 않는 그래프를 말한다. - 완전 그래프
정점들에 대한 가능한 모든 간선들을 가진 그래프를 말한다. - 부분 그래프
원래 그래프에서 일부 정점이나 간선을 제외한 그래프를 말한다.
그래프 말고 트리도 그래프입니다.
그래프를 1:N 구조로 만들고 상위 계층과 하위 계층을 만들어서 계층적 구조로 만든 형태가 트리입니다.
그 외에도 그래프들의 종류는 많으니, 한 번 찾아보시는 것을 추천드립니다.
경로
경로는 어떤 정점 A에서 시작해 다른 정점 B로 끝나는 순회로 두 정점 사이를 잇는 간선들을 순서대로 나열한 것입니다.
그래프는 N:M 관계이기 때문 A에서 B로 가는 경로는 여러개일 수 있습니다.
- 단순 경로
시작 정점과 끝 정점을 제외하고 중복된 정점이 없는 경로 - 싸이클 (
Cyclic)
경로의 시작 정점과 끝 정점이 같아서 순환의 구조가 나타나는 경로
인접
두 개의 정점에 간선이 존재하면 서로 인접(Adjacent)해 있다고 합니다.
완전 그래프 는 정점들에 대한 가능한 모든 간선들을 가지고 있기 때문에 해당 그래프의 임의의 두 정점은 서로 인접해 있다고 말할 수 있습니다.
인접 행렬
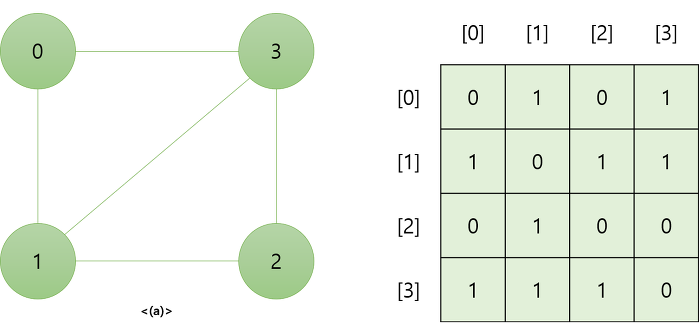
인접 행렬은 VxV 크기의 2차원 배열을 이용해 간선 정보를 저장한 배열을 이용해서 정점들 사이의 간선 정보를 저장합니다.
즉, 두 정점을 연결하는 간선의 유무를 행렬로 표현한 것입니다.
그래프에 가중치가 있는 그래프라면 해당 가중치를 나타낼 수 있는 배열 원소 타입을 사용해야 할 것이고, 가중치가 없는 그래프에서 인접 여부만 나타낸다면 인접인지 아닌지만 파악하면 되므로 boolean 으로도 충분합니다.
방향이 없는 그래프 에서 인접 행렬의 i 번째 행의 합은 i 번째 열의 합과 같고, 그것은 정점 V 의 차수를 뜻합니다.
반면 방향이 있는 그래프 에서 인접 행렬의 i 번째 행의 합은 정점 V 의 진출 차수를 뜻하고, i 번째 열의 합은 정점 V 의 진입 차수를 뜻합니다.
단점
만약 정점의 개수가 많지만, 인접된 정점들이 적을 때 배열은 굉장히 sparse 한 형태를 띄게 됩니다.
sparse 한 배열로 인접 행렬을 찾기 위해 탐색을 한다면, 인접된 정점들의 개수에 비해 탐색 계산에 대한 효율성이 떨어집니다.
인접 리스트
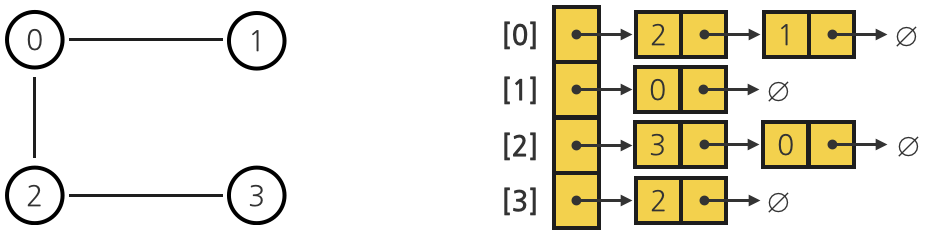
인접 리스트는 각 정점에 대한 인접 정점들을 순차적으로 표현한 리스트입니다.
하나의 정점에 대한 인접 정점들을 각각 노드로 하는 연결 리스트로 저장해 정점들을 관리합니다.
만약 인접 정점이 없는 정점이라면, 연결 리스트에는 head 만 존재할 것입니다.
방향이 없는 그래프 의 정점이 가진 연결 리스트의 size 는 해당 정점의 차수를 뜻합니다.
방향을 갖는 그래프 의 정점이 가진 연결 리스트의 size 는 해당 정점의 진출 차수입니다.
간선 리스트
간선 리스트는 두 정점에 대한 간선 그 자체를 객체로 표현해 리스트로 저장한 것입니다.
해당 간선의 시작 정점 과 끝 정점 의 정보를 저장해 리스트로 저장합니다.
마무리
오늘 백트래킹과 그래프를 공부하면서, 알고리즘의 최적화를 위해 생각해볼 것이 인상깊었습니다.
- 완전탐색을 진행할 때 백트래킹과 같이 가지를 칠 수 있는 부분이 있는지
- 중복 호출이 일어날 때 메모이제이션을 사용할 수 있는지
중복 호출이 일어날 수 있는 메소드의 로직에서 멤버 변수를 사용하지 않고 매개변수로만 로직을 실행할 때는 같은input을 받으면 동일한output을 결과로 만듭니다.
이 때 메모이제이션으로 저장해놓는다면 중복 호출 없이 시간적인 효율성을 가져갈 수 있을 것입니다. - 로직의 반복 횟수를 줄일 수 있는 아이디어
배열 돌리기와 같은 알고리즘을 풀어야할 때, 해당 배열이 몇 번이 돌아가면 제자리로 오는지와 같은 정보는 큰 입력값이 들어왔을 때 배열을 돌리는 횟수를 확연하게 줄여줄 수 있습니다.
위와 같은 부분을 알고리즘 로직을 생각해낼 때 한 번 씩 고려해본다면 효율적인 알고리즘을 구현할 수 있을 것 같습니다!
오늘 포스팅도 읽어주셔서 감사합니다 :)

