[Leet Code] Maximum Points You Can Obtain from Cards

기면지·2021년 5월 12일

Leet Code algorithm

LeetCode

목록 보기

4/20

안녕하세요 :)
오늘은 5월 2주차 4번째 알고리즘인 Maximum Points You Can Obtain from Cards 풀이를 적어보겠습니다.

문제

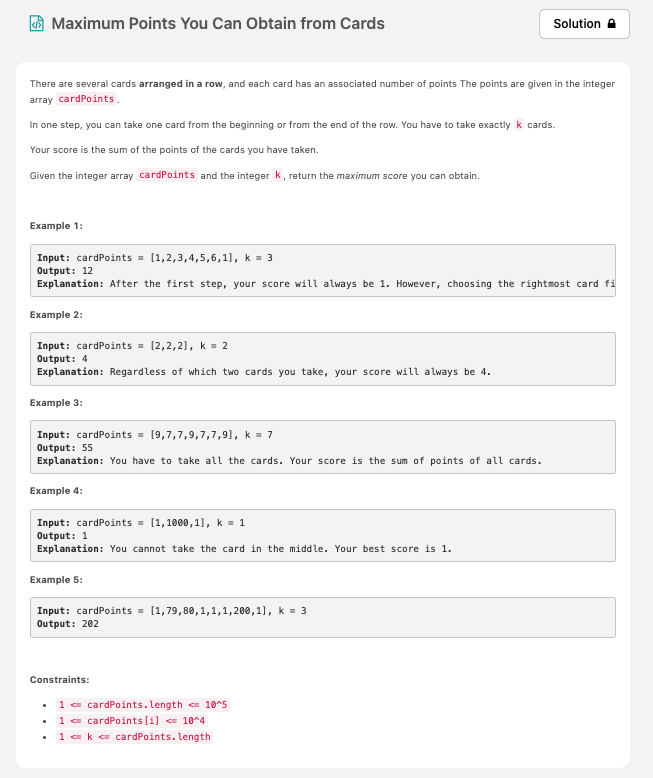
요약
주어진 cardPoints 배열에서 가장 처음 요소 또는 가장 마지막 요소를 포함하고, 연속된 위치에 있는 k 개의 수들 중 가장 큰 값을 찾아 return 하는 문제입니다.

처음 시도한 방법

이제 Leet Code를 몇 번 풀었다고 무작정 for문을 순회하는 코드는 생각하지 않았습니다. ~~(장족의 발전)~~

처음에는 무조건 처음 또는 끝에서만 시작하는 연속된 수라고 생각해서 왼쪽부터 요소들을 누적해서 저장하는 배열과 오른쪽부터 요소들을 누적해서 저장하는 배열 두 개를 만들어서 k 요소와 length-k 요소 중에 max를 return하도록 했습니다.

음.. 그런데 문제를 잘못 이해한 것을 Submit 버튼을 눌러보고 알았습니다.
잘못 도출되는 답이 있더라고요.

두번째로 시도한 방법

힌트는 아직 볼 단계가 아니라고 생각해서, 또 생각을 해봤습니다.

Time Limit를 마주치지 않기 위해서, 우선 처음과 끝으로부터의 k 번째 인덱스까지 누적 합을 구한 배열은 그대로 두었습니다.
그리고 max 를 구하는 방법을 바꾸었습니다.

그랬더니 Accept를 받았습니다!
너무 기뻤고,, 네,, 힌트를 보지 않고 푼 최초의 문제가 되었습니다.
이제부터 그 방법을 설명하겠습니다.

코드 설명

int max = 0;
int[] leftSumArr = new int[k + 1];
int[] rightSumArr = new int[k + 1];

leftSumArr[1] = cardPoints[0];
rightSumArr[1] = cardPoints[cardPoints.length - 1];

최대값을 비교할 max 변수와 왼쪽부터 누적 합을 저장하는 leftSumArr , 오른쪽부터 누적 합을 저장하는 rightSumArr 를 선언해주었습니다.

그리고 누적 합의 배열의 길이는 k+1 로 설정하고, 1부터 누적 합을 저장했습니다.
그래서, 1번 인덱스에는 cardPoints 의 처음과 끝 값이 저장됩니다.

for (int i = 1; i <= k; i++) {
    leftSumArr[i] = leftSumArr[i - 1] + cardPoints[i - 1];
    rightSumArr[i] = rightSumArr[i - 1] + cardPoints[cardPoints.length - i];
}

계속 언급했던 것처럼 누적 합이므로, 구할 인덱스의 이전 인덱스와 cardPoints 값을 더해주면 됩니다.

cardPoints 가 [1, 2, 3, 4, 5, 1] 이고 k 가 3이라면,
leftSumArr 는 [0, 1, 3, 6]이 되고
rightSumArr 는 [0, 1, 6, 10]이 됩니다.

이 다음에서, max 값을 구하는 방법이 나옵니다.

for (int i = 0; i <= k; i++) {
    max = Math.max(max, leftSumArr[i] + rightSumArr[k - i]);
}

leftSumArr 와 rightSumArr 의 값을 더해서 비교해줍니다.

위의 예시와 이어서 생각하면,
0+10 vs 1+6 vs 3+1 vs 6+0
이 되는 것입니다.

이렇게 max 값을 구하면, 모든 경우를 생각하면서도 깔끔한 코드로 구할 수 있습니다!

전체 코드

class Solution {
    public int maxScore(int[] cardPoints, int k) {
        int max = 0;
        int[] leftSumArr = new int[k + 1];
        int[] rightSumArr = new int[k + 1];

        leftSumArr[1] = cardPoints[0];
        rightSumArr[1] = cardPoints[cardPoints.length - 1];

        for (int i = 1; i <= k; i++) {
            leftSumArr[i] = leftSumArr[i - 1] + cardPoints[i - 1];
            rightSumArr[i] = rightSumArr[i - 1] + cardPoints[cardPoints.length - i];
        }

        for (int i = 0; i <= k; i++) {
            max = Math.max(max, leftSumArr[i] + rightSumArr[k - i]);
        }

        return max;
    }
}