머신러닝에 관련된 책이나 글을 보다보면 정보이론에 대해 심심치 않게 볼 수 있다.
이번에는 정보이론에 대해서 최대한 간단하게 정리해보려 한다.
정보량
핵심은 자주 발생하는 사건 보다 자주 발생하지 않는 사건에서 정보량이 더 높다는 것이다.
정보이론에서 정보량은 로 나타낼 수 있다.
결과적으로 0과 1사이의 값을 가지는 확률에 -log를 취했기 때문에 확률이 적을수록 즉, 자주 발생하지 않는 사건일수록 얻는 정보량은 커지게 된다. log의 밑은 정보의 단위를 의미하게 되며 2를 사용할 경우를 비트(bit) 혹은 섀넌이라고 부르며 자연상수일 경우 내트(nat)라고 한다.
엔트로피
엔트로피는 정보량의 기대값을 의미한다. 기대값이란 어떤 사건이 벌어졌을때 이득과 그 확률을 곱한 것을 전체 사건에 대해 합한 것이다. 정의는 다소 어렵게 되어 있지만 쉽게 생각해 평균의 의미로 볼 수 있다. 하나의 예를 들어보자.
주사위를 던졌을 때 나오는 숫자가 내 점수라고 할때 주사위를 던져 얻을 수 있는 기대값은 몇일까?
주사위를 1부터 6까지 나올 수 있는 확률은 으로 같은 것은 알 수 있다.
위에서 설명한 기대값의 정의대로 풀어서 써보면 아래와 같다.
위의 식을 조금만 바꿔보자.
이 식은 우리가 흔히 사용하는 산술평균과 같다. 따라서 기대값을 평균의 의미로 볼 수 있다는 것이다.
결과적으로 주사위를 던졌을 때 얻을 수 있는 점수로 3.5점을 기대해 볼 수 있게 된다.
그렇다면 엔트로피라고 불리는 정보량의 기대값의 식은 어떨까?
$
엔트로피는 위와 같이 나타낼 수 있다.
위에서 배운 기대값으로 식을 정리하면 다음과 같이 쓸 수 있다.
처음 엔트로피라는 단어를 접했을 때 비전공자인 나는 열역학의 엔트로피가 먼저 떠올랐다.
열역학에서의 엔트로피에서 키워드는 무질서도이다. 서로 다른 계에 대해 명확하게 구분이 되는 정도로 무질서도가 높다면 구분이 쉽게 되지 않는것으로 이해할 수 있다. 쉽게 생각해 물에 잉크를 떨어뜨리면 점점 잉크가 물전체로 퍼지며 이 현상을 무질서도가 증가했다고 한다.
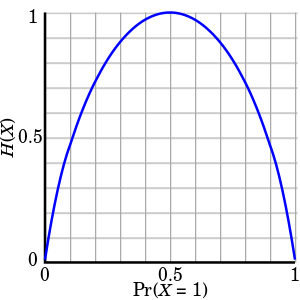
이처럼 정보이론에서의 엔트로피는 불확실성이라는 키워드를 사용한다. 두 학문에서 다른 단어로 사용하지만 그 본질은 같다고 생각한다. 불확실성이 높다는 것은 어떤 사건들이 구분이 잘 되지 않는 경우를 뜻하며 불확실성이 높으려면 여러 사건들이 일어날 확률이 균등하면 된다.
위 그래프의 x축을 동전의 앞면이 나올 확률이라고 할때 0.5의 확률을 가질때가 가장 높은 엔트로피를 가진다. 가령 동전의 형태가 변형되어 확률이 어느 한쪽으로 치우치는 순간 엔트로피는 낮아지는 것을 볼 수 있다.
크로스 엔트로피
실제 데이터 분포 와 새로운 분포 를 이용하여 구하는 엔트로피를 크로스 엔트로피라고 한다. 식은 아래와 같다.
딥러닝 모델을 학습할 때 크로스 엔트로피는 오차함수로 사용하여 엔트로피 값을 최소화 하려는 방향으로 학습하게 된다. 이 의미를 이해하기 위해 먼저 KLD에 대해 알아야 한다.
쿨백-라이블러 발산(Kullback-Leibler Divergence, KLD)
KLD는 두 확률분포의 차이를 나타낼때 사용한다. 식은 아래와 같다.
만약 P와 Q가 동일한 확률분포를 가진다면 이 값은 0이된다.
이 식을 풀어보면 아래와 같다.
KLD는 크로스 엔트로피와 매우 밀접한 관련이 있음을 알 수 있다.
크로스 엔트로피값을 낮추는 방향으로 학습을 한다는 것은
위의 식에서 실제 데이터의 분포는 변하지 않기 때문에 KLD를 낮추는 것을 의미하게 되고 KLD의 의미에 따라 두 분포의 차이를 최소화하는 방향으로 학습을 시킨다고 이해할 수 있다.