[백준] 7453번 합이 0인 네 정수 (C++)

https://www.acmicpc.net/problem/7453

이 문제는 완전탐색을 하게 될 경우 4000^4가 되어 시간 복잡도를 초과하게 된다.
그래서 문제를 풀 때 a,b / c,d 로 묶어서 시간복잡도가 초과되지 않게 해결했다.

a,b / c,d의 합을 미리 구해준 뒤, sort를 통해 정렬해준다.
그 이후, 투 포인터를 적용해서 풀었다.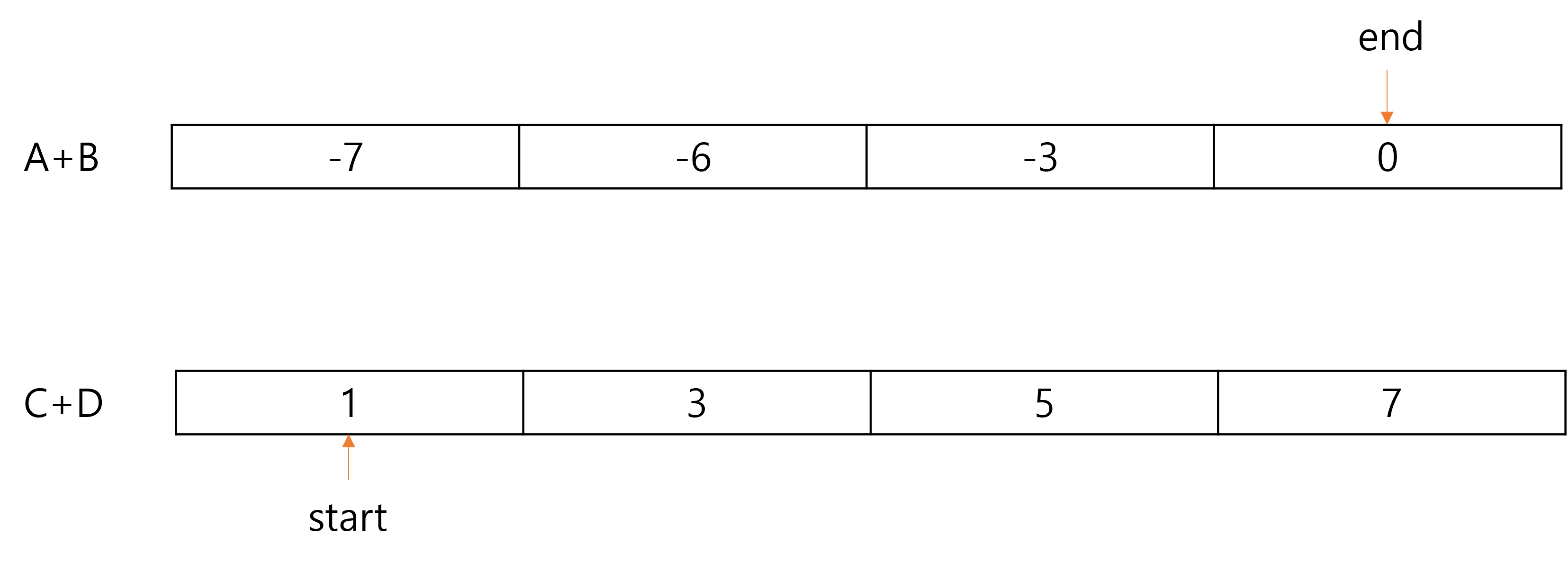
이 경우엔 3가지 상황이 있다.

1. start와 end의 합이 0보다 클 경우

-> 이 경우는 end의 인덱스를 -1 해준다.

2. start와 end의 합이 0보다 작을 경우

-> 이 경우는 start의 인덱스를 +1 해준다.

3. start와 end의 합이 0일 경우

-> 결과 값을 1 더해준다.

하지만, 이렇게 하면 중복된 값의 처리가 불가능해진다.

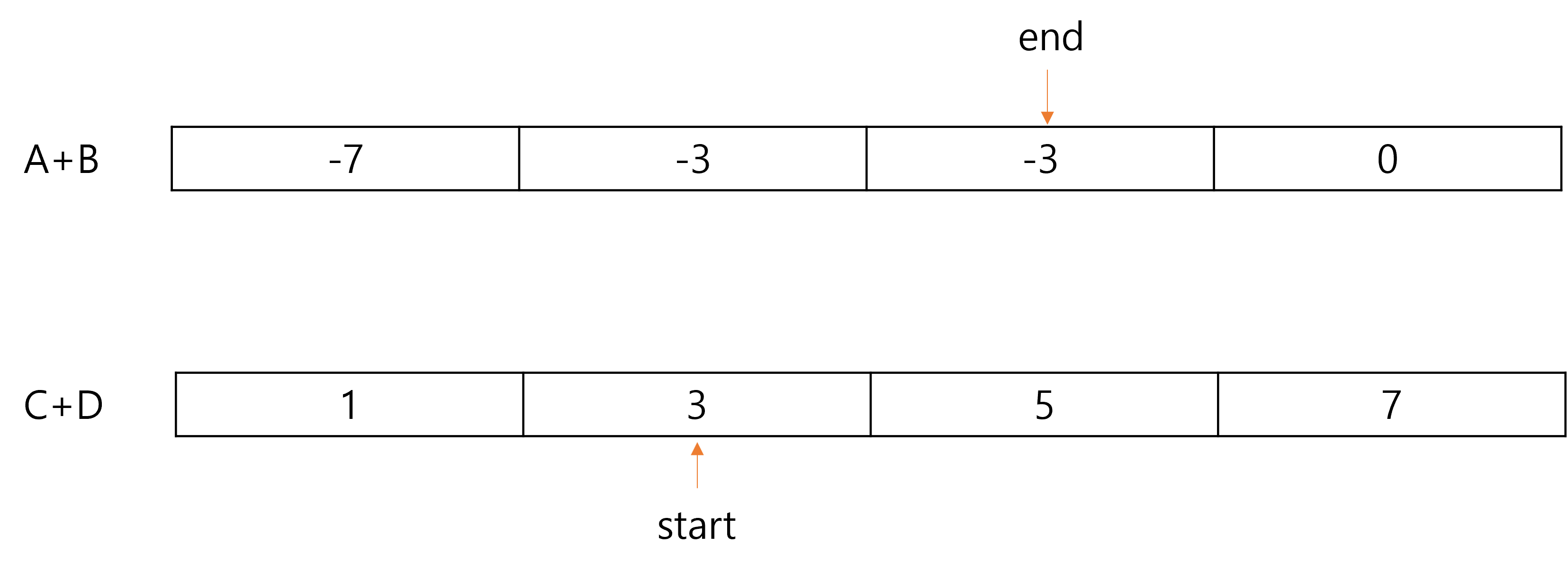
아래와 같은 상황에서 3과 -3이 만났으니 결과 값을 하나 더해주는데 어느 인덱스를 바꿔줘야 하는지 고민을 하다가 upper_bound, lower_bound를 사용했다.

즉, 합이 0이 나오게 될 경우
결과 값은 (upper_bound 인덱스 - start 인덱스) * (end 인덱스 - lower_bound 인덱스 + 1) 값을 더해주면 된다.
이와 같은 방법으로 중복을 처리해주니 문제가 해결됐다.

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

vector<long long> sum1;
vector<long long> sum2;
int n;
long long a[4001];
long long b[4001];
long long c[4001];
long long d[4001];

int main() {
	cin.tie(0); cout.tie(0);
	ios_base::sync_with_stdio(false);
	cin >> n;
	for (int i = 0; i < n; i++) {
		cin >> a[i]; cin >> b[i];
		cin >> c[i]; cin >> d[i];
	}
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			sum1.push_back(a[i] + b[j]);
		}
	}
	long long ret = 0;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			sum2.push_back(c[i] + d[j]);
		}
	}

	sort(sum1.begin(), sum1.end());
	sort(sum2.begin(), sum2.end());
	long long s = 0; long long e = sum2.size() - 1;
	while (s < sum1.size() && e >= 0) {
		long long sum = sum1[s] + sum2[e];
		if (sum == 0) {
			long long u = upper_bound(sum1.begin(), sum1.end(), sum1[s]) - sum1.begin();
			long long l = lower_bound(sum2.begin(), sum2.end(), sum2[e]) - sum2.begin();
			ret += (u - s) * (e - l + 1);
			s = u;
			e = l - 1;
		}
		else if (sum > 0) e--;
		else s++;
	}


	cout << ret;
}