🎯문제
https://www.acmicpc.net/problem/1655

백준이가 동생에게 수를 외치는 상황마다 중앙값을 말해야 하는 문제이다.
🏳️접근
그렇다면 백준이가 외치는 수를 정렬된 배열로 가지고 있고, 그 중에서 중앙 값을 구해야 한다.
시간 제한이 굉장히 짧기 때문에, 일반적인 Arrays.sort() 메서드를 이용하지는 못할 것이라고 생각했고, heap구조를 이용해야겠다고 생각했다.
하지만 heap자료구조인 우선순위 큐 클래스를 이용한다고 해도, 매번 절반을 뺐다가 넣었다가 하지는 못할 것이라고 생각해서, 직접 heapSort를 구현하고, heapSort 내부에 로직을 추가하는 것으로 해결할 수 있을 것이라고 생각했다.
하지만 Heap을 만든다고 하여도, 계층 형태에서의 크기 비교는 보장하지만, 같은 depth에 있는 값들의 순서까지 보장하지는 않았다.
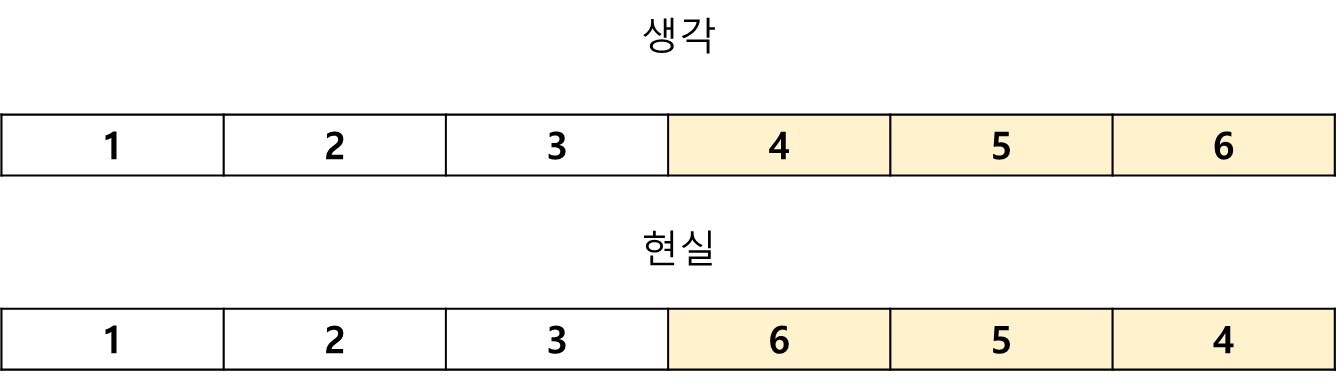
그래서 각 depth를 로그 함수로 구한 이후, 해당 depth의 끝까지 정렬을 하면 되지 않을까? 생각을 했다.
대략 아래와 같은 식으로 풀면 정렬된 Heap을 가질 수 있다고 생각했다.
private static int log2(int depth){
return (int) (Math.log(depth) / Math.log(2));
}
private static void heapify(int k){
...
int log2 = log2(k);
int currentDepth = (int)(Math.pow(2,log2));
int maxDepth = Math.min((int)(Math.pow(2,log2+1))-1, top);
Arrays.sort(heap, currentDepth, maxDepth);
...
}
하지만 결국 매번 정렬이 들어가게 되었고 주어진 시간 제한을 통과하지 못할 것이라고 생각하고 포기했다...
💯해답
다른 분들의 풀이 방법을 확인하니 2개의 우선순위 큐를 활용해서 중앙 값을 구하는 것을 확인했다.
그 방법은 하나의 정렬된 배열을 두 개의 우선순위 큐를 통해 구현을 하고, minHeap과 maxHeap으로 만들고, root가 중앙을 가리키게 해놓는 방식으로 중앙 값을 구현하는 것을 확인했다.

위와 같은 형태로 구현을 했다. Heap의 특성상 root를 제외한 나머지 값들의 명확한 순서를 보장하지는 않지만, 문제에서 필요한 것은 중앙 값이기 때문에 그 부분은 중요하지 않은 것 같다.
사람들이 사용한 로직은 아래와 같다.
- 두 Heap의 Size가 같다면, MaxHeap에 새로운 값을 추가한다.
- Heap의 Size가 다르다면, MinHeap에 새로운 값을 추가한다.
- 1,2 과정을 진행 후, 두 Heap의 root를 비교하고, 정렬에 맞지 않다면(MaxHeap의 root가 MinHeap의 root보다 크다면) 둘을 swap한다.
🖥️코드
다른 분들의 풀이 로직을 확인하고 코드를 작성하였다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.PriorityQueue;
class Main {
static StringBuilder sb = new StringBuilder();
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
PriorityQueue<Integer> minHeap = new PriorityQueue<>();
PriorityQueue<Integer> maxHeap = new PriorityQueue<>((x, y) -> y - x);
for (int i = 0; i < n; i++) {
int k = Integer.parseInt(br.readLine());
if (maxHeap.size() == minHeap.size())
maxHeap.add(k);
else
minHeap.add(k);
if (!minHeap.isEmpty() && minHeap.peek() < maxHeap.peek()) {
int min = minHeap.poll();
int max = maxHeap.poll();
minHeap.add(max);
maxHeap.add(min);
}
sb.append(maxHeap.peek()).append("\n");
}
System.out.println(sb);
}
}중앙 값을 구할 때, 두개의 우선순위 큐를 활용해서 구할 수 있다는 사실을 새로 알 수 있었다.
📚참고 자료
https://nyang-in.tistory.com/268
https://nyang-in.tistory.com/155
https://gh402.tistory.com/32
https://dragon-h.tistory.com/6
