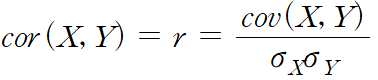1. Vector/Matrix
1.1 Vector(벡터)
https://youtu.be/ArgTeYVuJUo
벡터는 숫자 자료를 '배열'한 것. 그럼 배열은? 리스트의 자료 구조(Data Structure)의 형태
알고리즘에서는 데이터를 분석하기 위해 데이터가 정렬된 벡터 형태를 필요로 한다.
예) 집 값 분석 [크기, 가격] != [가격, 크기] (여기서는 2차원(=숫자가 두 줄로 배열). 벡터임) 각 위치에 따라 나타내는 의미가 다르기 때문에 순서가 중요하다.
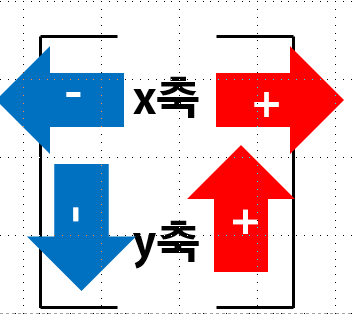
2차원 벡터: 원점에서 뻗어나가는 화살표(크기 + 방향)라 생각하면 이해하기 쉽다. 벡터의 좌표는 한 쌍의 숫자. 기본적으로 벡터의 머리가 꼬리(원점)로부터 얼마나 떨어져 있느냐를 의미한다.
x축에 따라 움직인다. y축에 나란히 움직인다.
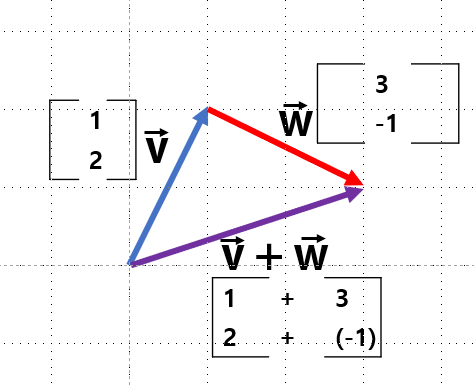
삼각형법: 좌표계 위의 벡터의 덧셈
스칼라: 크기만 있고 방향은 없음. 벡터의 내적, 단일 숫자. 실수, 정수 모두 가능
상수배: 곱해주는 수: 스칼라, 상수배, 스칼라배 각 항에 그 스칼라를 곱해라.
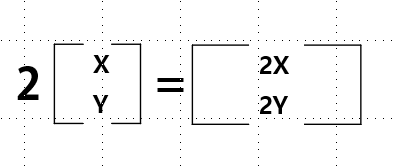
벡터의 길이(length)는 벡터의 차원수와 동일하다
데이터 사이언스에서는 벡터를 왜 배워야 하나? : 시각적으로 데이터를 이해할 수 있도록 도움을 주거나 그 반대의 경우를 위해서(?), 모든 데이터는 행, 열 vector로 다 나타낼 수 있다.
1.1.1 벡터의 크기(Magnitude, Norm, Length)
벡터의 Norm, Magnitude는 단순한 길이(선). 그렇기에 피타고라스 정리(직각 삼각형의 밑변을 구하는 것)로도 길이를 구할 수 있다.
벡터의 크기를 표현 할 때 ||를 사용. 즉, 벡터의 크기는 '모든 원소의 제곱을 더한 후 루트'
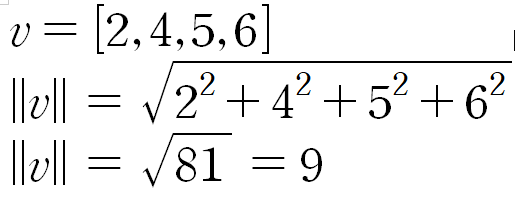
벡터의 특징

1.1.2 벡터의 내적(Dot Product)
두 벡터의 내적은 각 구성요소를 곱한 뒤 합한 값과 같다.
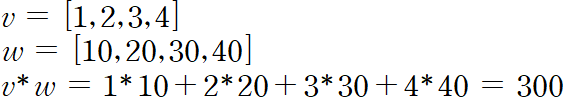
내적의 교환법칙: a b = b a
내적의 분배법칙: a (b+c) = a b + a * c
벡터의 내적을 위해서는 두 벡터의 길이가 반드시 같아야 한다.
1.2 Matrix(행렬)
매트릭스란 행과 열을 통해 배치된 숫자들. 매트릭스를 표현하는 변수는 일반적으로 대문자를 사용한다. X, Y, Z
Dimensionality,매트릭스의 행과 열의 개수를 차원(Dimension, 차원수 등)이라 표현한다. (행-열)(가로로 긋는 갯수-세로로 긋는 갯수)
행렬의 곱
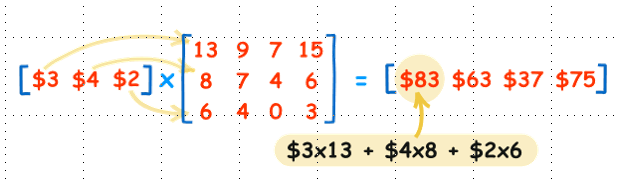
Regression (Section 2에서 배움): 회귀모형
Dimensionality Reduction(PCA, SVD 등): 사이즈가 큰 데이터셋을 사이즈가 작은 부분으로 나누는 작업. 보통은 시각화를 위해서 하거나 다른 모델에 적용시키기 위해서 사용한다.
4차원을 표현하더라도 우리는 이해하기 어려움. 15차원은?? 그렇기에 차원을 줄여서 이해할 수 있도록 '시각화'하기 위해 사용한다.
딥러닝: CNN(Section 4에서 배움): Convolving은 필터, 커널을 통해 이미지를 축소, 그 결과물을 분석에 사용하는 방법. 필터를 통해서 수정된 이미지는 특수한 부분이 강조되어 이미지 분석에 사용될 수 있다. 완전히 선형대수를 기반으로 함.
1.2.1 Transpose(전치)
행과 열을 바꾸는 것을 의미한다. 보통은 T나 '을 사용하여 표현한다.대각선 부분의 구성요소를 고정시키고 이를 기준으로 나머지 요소를 뒤집는다고 생각하면 좋다.
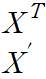
1.2.2 Square matrix(정사각 매트릭스)
정방 매트릭스라고도 불리며 아주 기초적인 매트릭스다. 형과 열의 개수가 동일한 매트릭스.
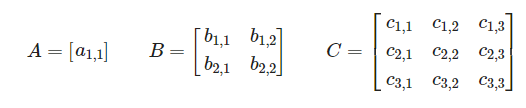
Diagonal(대각) 대각선에만 값이 있고 나머지는 0
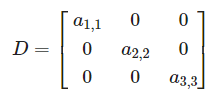
Upper Triangular(상삼각) 대각선 위에만 값이 있고 나머지는 0
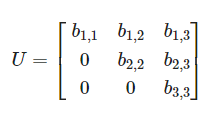
Lower Triangular(하삼각) 상삼각과 반대로 대각선 아래에만 값이 있다.

Identity(단위 매트릭스) 대각 매트릭스 중 모든 값이 1인 경우. 어떤 정사각 매트릭스에 단위 행렬을 곱하면 그 결과값은 원본 정사각 매트릭스로 나온다. 반대로 어떤 매트릭스에 A를 곱했을 때 단위 매트릭스가 나오게하는 매트릭스 A를 역행렬(Inverse)이라 부른다.
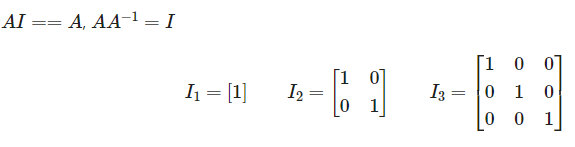
Symmetric(대칭) 대각선을 기준으로 위 아래의 값이 대칭인 경우
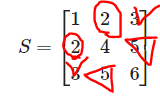
1.2.3 Determinant(행렬식)
모든 정사각 매트릭스가 가지는 속성으로 det(a) 혹은 |A|로 표현. (매트릭스 A에 대해 ||A||는 A의 행렬식(||)을 절대값(||)으로 나타내라는 의미)
정사각 행렬에 스칼라를 대응시키는 함수의 하나. 2*2는 직접 계산할 수 있겠지만

1.2.4 Inverse(역행렬)
행렬 * 역행렬 = 1(단위 매트릭스)
매트릭스의 곱은 있지만 나눗셈은 없다. 대신 그 행렬의 역행렬을 곱해준다.
행렬식이 0인 경우: 특이(Singular) 매트릭스라고 부르기도 한다. 2개의 행 혹은 열이 선형 관계를 이루고 있을 때 발생한다.
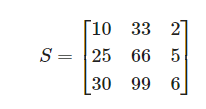
2. Linear Algebra +
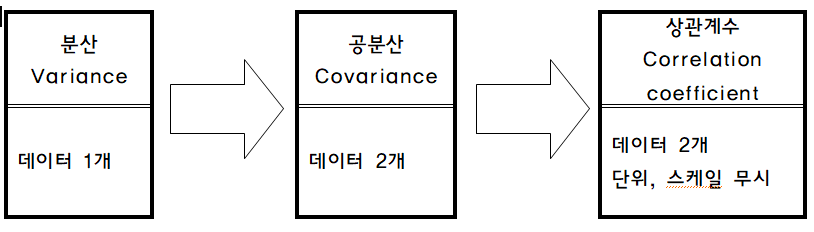
2.1. Variance(분산)
분산은 데이터가 얼마나 퍼져있는지를 측정하는 방법 중 하나. 각 값들의 평균으로부터 차이의 제곱 평균.
2.2 Standard Deviation(표준 편차)
분산의 제곱근(루트를 씌운다.) 분산을 구할 때에 제곱 값들을 활용했다. 그래서 평균에 비해 그 스케일(수의 크기)이 커지는 문제가 있다. 표준 편차는 이러한 문제를 해결하기 위해 제곱된 스케일을 낮춰주는 방법. 이러한 이유로 표준 편차를 많이 활용한다.
2.3 Covariance(공분산)
1개의 변수 값이 바뀔 때에 다른 변수가 어떤 연관성을 가지고 변화하는 지를 알아내는 것. 2개의 확률 변수의 선형 관계를 나타내는 값. 즉, 두 변수 사이의 연관성을 나타내준다.
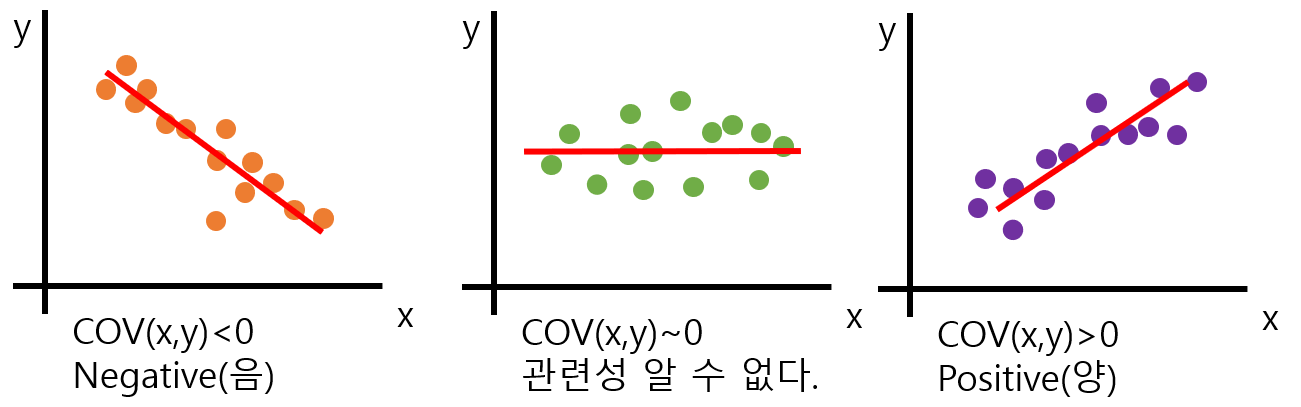
큰 값의 공분산은 두 변수 사이가 큰 연관성을 나타내고 있다고 볼 수 있다. 하지만, 변수들이 서로 다른 스케일을 가지고 있다면 공분산은 실제의 연관성에 관계없이 영향을 받게 된다. 바꾸어 말하자면, 두 변수의 연관성이 적더라도 큰 스케일을 가진다면 큰 값이 나오게 된다는 의미.
2.3.1 Variance-covariance Matrix(분산-공분산 매트릭스)
분산-공분산 매트릭스를 통해 2차원 이상에서의 데이터의 분포를 확인 가능하다.
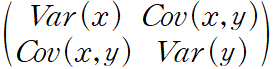
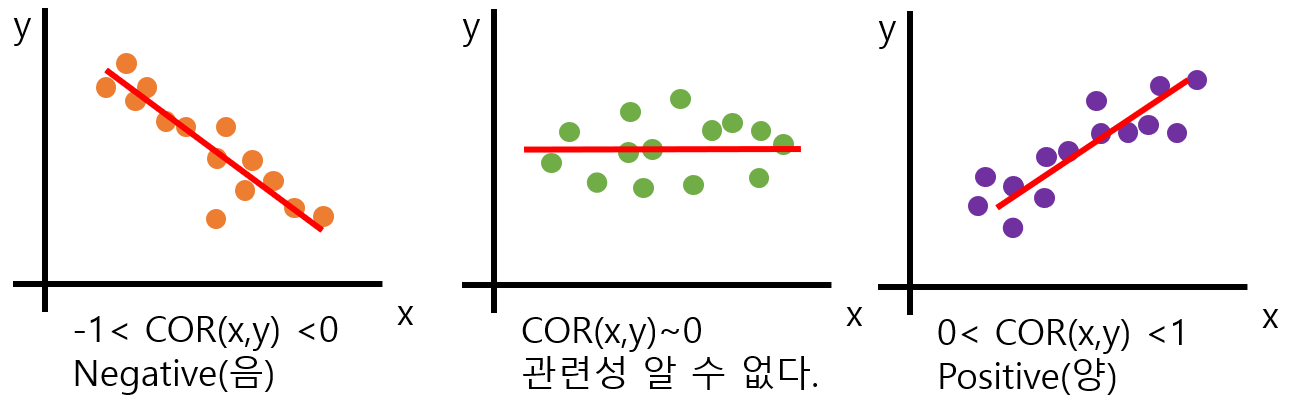
2.3.2 Correlation coefficient(상관계수)
분산에서 스케일에 의한 문제를 해결하기 위해 표준 편차를 사용했던 것처럼 공분산의 스케일을 조정해줄 수 있다.
공분산을 두 변수의 표준편차로 각각 나누어 주면 해결 가능! 그 결과 값을 상관계수라고 부른다.
-1(Negative, 음) <= 상관계수 <= 1(Positive, 양)
상관계수는 대체로 공분산에 비해 더 좋은 지표로 활용된다. 그 이유는 상관계수의 범위가 -1 ~ +1까지의 범위가 정해져 있기 때문에. 또 공분산은 스케일, 단위의 영향을 받지만 상관계수는 받지 아니한다. 즉 상관계수는 데이터의 평균이나 분산 등에 영향을 받지 않는다.
2.4 Orthogonality(수직성)
벡터나 매트릭스가 서로 수직으로 있는 상태를 말한다.
아래 그림을 보자. 좌표상에 있는 거의 모든 벡터는 다른 벡터와 (아주 작게라도) 상관이 있다. 하지만 수직의 관계에 있는 벡터는 전혀 상관관계가 없다.
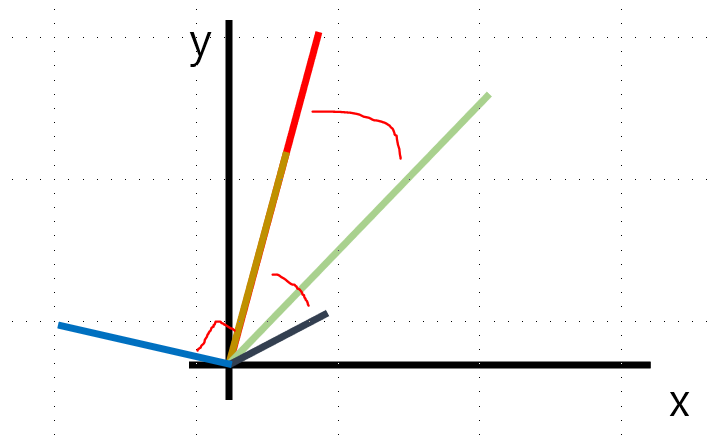
임의의 두 벡터의 내적 값이 0이라면 서로 수직인 상태다.
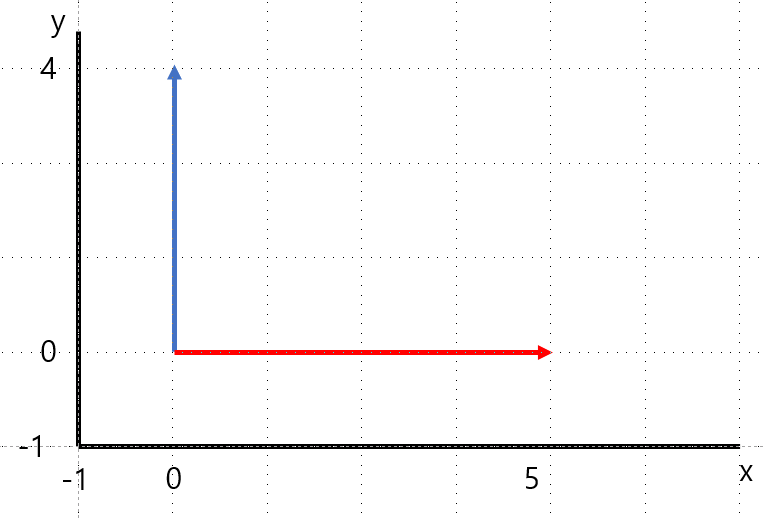
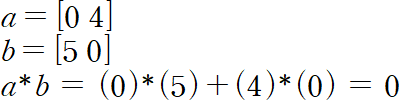
2.5 Unit Vectors(단위 벡터)
단위 길이(1)를 가지는 모든 벡터
왜 중요하냐면 모든 벡터(혹은 매트릭스)는 단위 벡터의 선형 조합(스칼라곱, 벡터합)으로 표기되기 때문. 아래와 같이 표현 가능
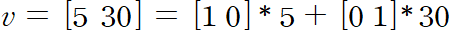
2.6 Span
주어진 두 벡터의 합 혹은 차와 같은 조합으로 만들 수 있는 모든 가능한 벡터의 집합
2.6.1 선형 관계의 벡터(Linearly dependent Vector)
두 벡터가 같은 선상에 있는 경우 이 벡터들은 선형 관계에 있다고 표현한다.
그렇기에 이 두 벡터의 조합을 통해서 선 외부의 새로운 벡터를 생성할 수 없다.
즉, 이미 올려져 있는 선으로 벡터의 span이 제한된다.
2.6.2 선형 관계가 없는 벡터(Linearly independect Vectors)
같은 선에 없는 벡터들은 선형적으로 독립되어 있다고 말한다.
주어진 공간의 모든 벡터 조합을 통해 만들어 낼 수 있다.
2.7 Basis
벡터 공간 V의 basis는 V라는 공간을 채울 수 있는 선형 관계에 있지 않은 벡터들의 모음(span의 반대 개념)
Orthogonal Basis: Basis에 추가로 Orthogonal(직교) 조건이 붇는 서로 수직인 벡터들
Orthonormal Basis: Orthogonal + Normalized 길이가 서로 1인 벡터들
2.8 Rank
매트릭스의 Rank는 매트릭스의 행 또는 열을 이루고 있는 벡터들로 만들 수 있는 span의 차원
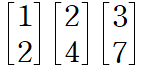
위의 그림에서는 Vector는 3이지만, Rank는 2가 나온다. [1, 2]*2는 [2, 4]가 나온다.
Data에서의 의미: 벡터끼리 선형관계가 있다는 것은 "두 데이터가 가지고 있는 의미는 동일하다" 그러나 무수히 많은 데이터들을 살펴볼 때 단위, 스케일 등만 달라서 마치 다른 데이터로 보일 수 있다.
그럴 때에는?: 분석 방법을 수정하거나, 데이터를 다시 수집해야 한다.
알아내는 법은?: 직접 계산을 해보거나, numpy.linalg.matrix-rank 함수 활용해본다.
2.9 Linear Projection
선에 투영시키는 것.
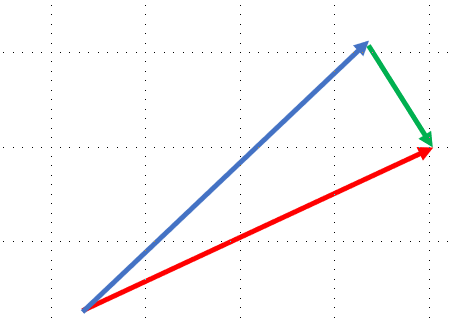
파란색 선을 빨간색 선으로 투영시킨다.(초록과 빨강은 직교)
필요한 이유?: 기존의 파란 선을 표현하기 위해서는 x, y축 2 개의 feature가 필요하다. 하지만 projection을 하면 기존 파란 선을 표현하기 위해 x축, 1 개의 feature만 필요하게 된다.
단점: 대신 초록 선 만큼의 loss가 일어나게 된다.
장점: data를 저장하기 위한 메모리가 줄어든다.(메모리 사용이 줄어드는 건 좋은 일!)