자료구조 & 알고리즘
1.그리디 알고리즘 & 구현 1

문제를 해결할 때 값이 k로 나누어 떨어지면 나눗셈을, 그렇지 않으면 -1을 수행하여 최소한의 횟수로 1에 도달하게 구현하였다.
2.그리디 & 구현 2

정렬을 한후 낮은 공포도의 모험가부터 공포도와 배열의 원소개수를 비교를 통해 배열을 형성할지, 말지를 통해 결과적인 횟수를 구할 수 있었다.
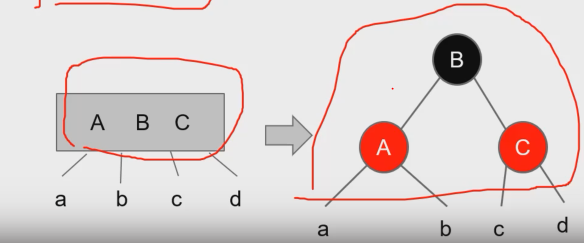
3.탐색트리I
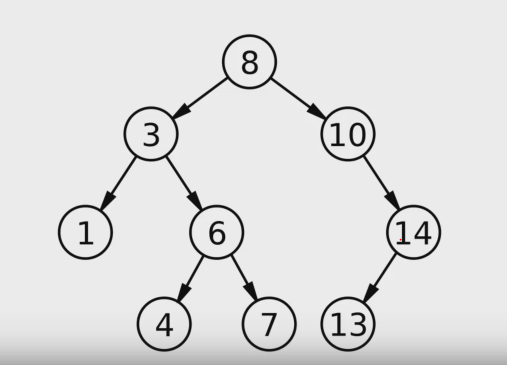
내가 어떤 하고싶은 것이 있을 때 효율적으로 처리해주는 것수학의 '집합'개념 이용집합에 대한 연산membership query \- 어떤 원소가 집합의 원소인지 판단하는것insertion \- 생성자deletion \- 빼다가 전부빼면 공집합, 소멸자배열O(N)
4.B-Tree
대용량 데이터는 HDD등에 저장됨Seek time : 헤드를 원하는 데이터가 섹터로 이동하는데 걸리는 시간운이 좋으면 현재 헤드 밑에 원하는 섹터운이 나쁘면 현재 헤드 바로 앞에 원하는 섹터rpm : 분당 회전 속도:7200rpm ~=0.01sec데이터는 블럭 단위로
5.해시 테이블

탐색을 지원하는 집합을 구현하는 방법O(log n)보다 빨리 풀 수 있는 방법 : 해시테이블 O(n)1~n 사이의 수 k 개가 원소인 집합 구현 시N이 무지 크다면? 메모리를 엄청 낭비하게 된다.원소가 저장될 자리가 원소의 값에 의해 바로 o(1) 로 결정되는 자료 구
6.그리디 알고리즘

그리디 알고리즘매 단계마다, 각 단계에서 최선이라고 볼 수 있는 선택을 하는 것전체적인 입장을 보지 않고 순간 최선을 취한다.알고리즘이 매우 간단한 대신, 구한 답이 정답이라는 보장은 없다.정답을 알려면 증명이 필요하다.기본형태 \- C : 후보들의 집합 \- S
7.분할 상환 기법
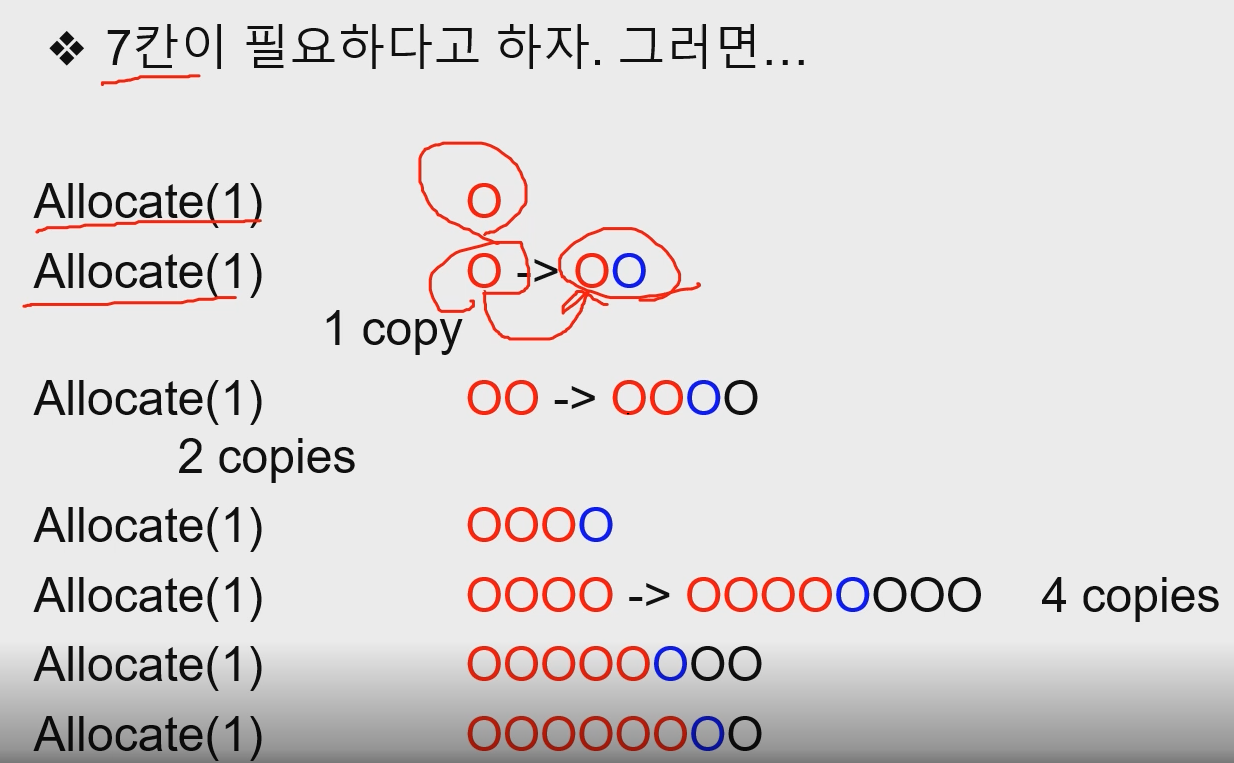
분할상환 기법알고리즘의 시간복잡도를 측정하는 방법 \- 지금까지의 최악의 경우를 고려하고, 이때의 시간/공간 비용을 고려함 \-어떤 연산은 다른 연산에 비해 시간이 많이 소요된다.어떻게 측정할 것인가 \- 상한 : 최악의 경우시간 \* 연산의 횟수 \-필요한 연
8.그래프 알고리즘I
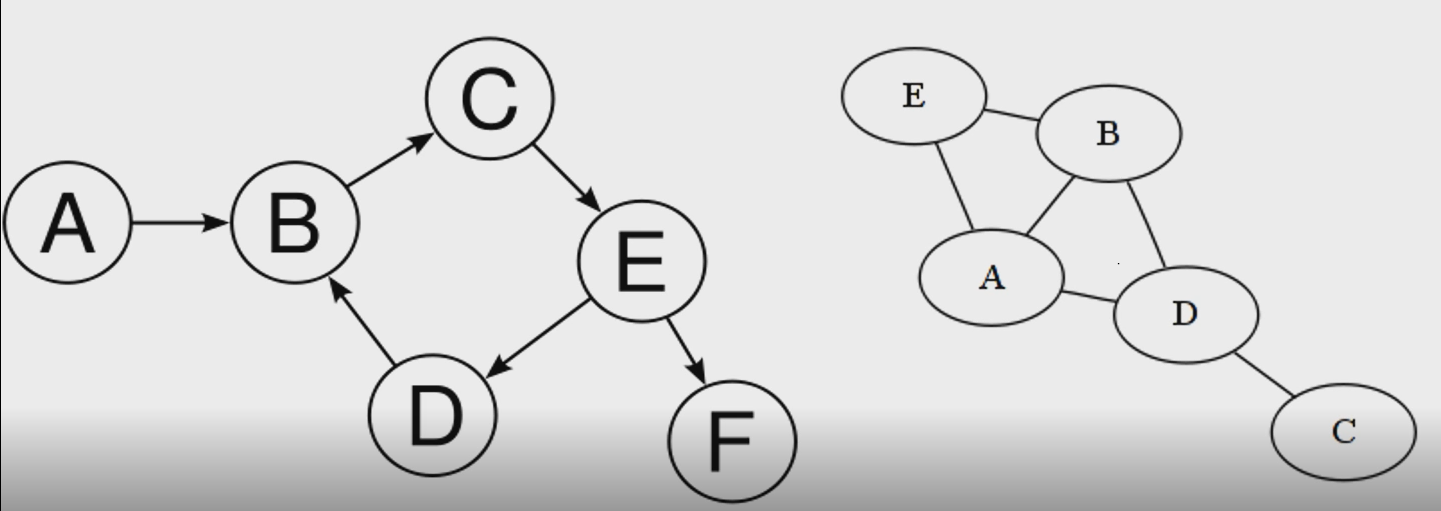
그래프V : 노드의 집합E : 에지의 집합E는 VxV 의 부분집합(노드와 노드만을 이을 수 있다.유향 그래프 VS 무향 그래프에지의 방향이 있으면 유향 그래프, 없으면 무향 그래프(순서에 의미가 있다.)무향 그래프는 양방향 유향 그래프로 생각할 수 있다.가중 그래프(w
9.그래프 알고리즘 II
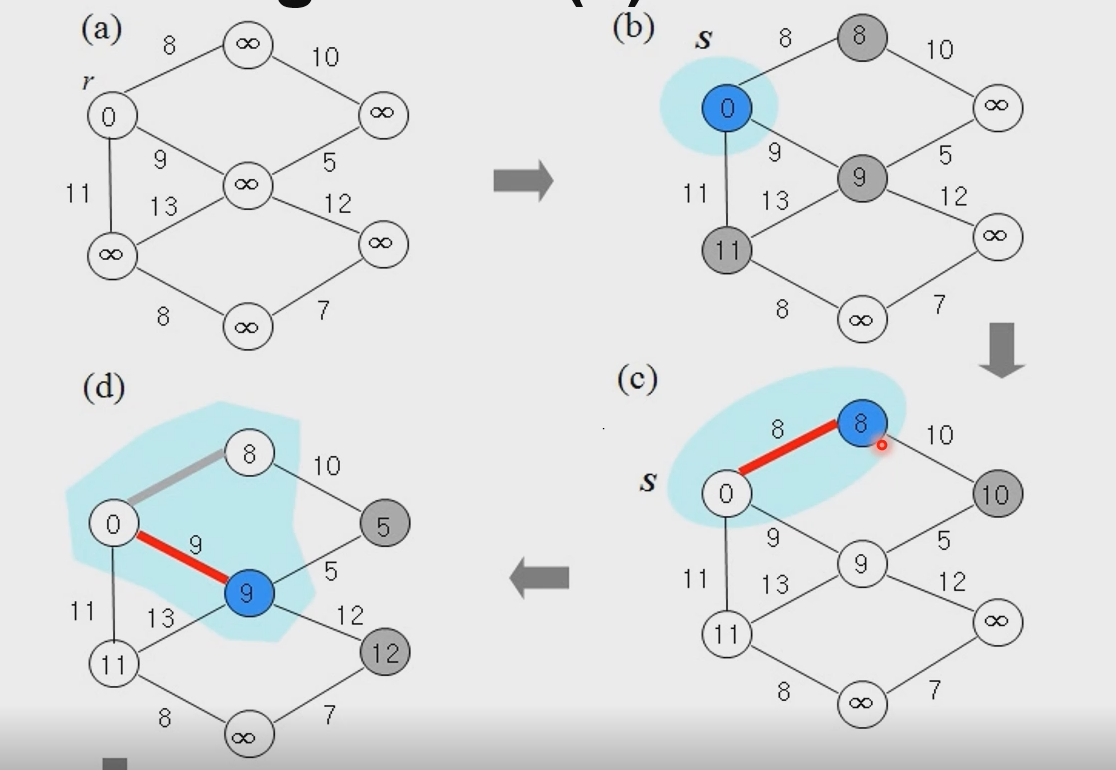
최소신장 트리신장트리 : 그래프 g의 노드 v를 모두 포함하는 e에 속하는 에지를 사용하여 만든 트리최소 신장 트리 : 가중 그래프 g 의 신장트리 중에서 트리에 속한 가중치의 합이 가장 작은 신장 트리신장 트리를 만드는 방법\-Prim's algorithm \-Kr
10.최단경로 & 다익스트라
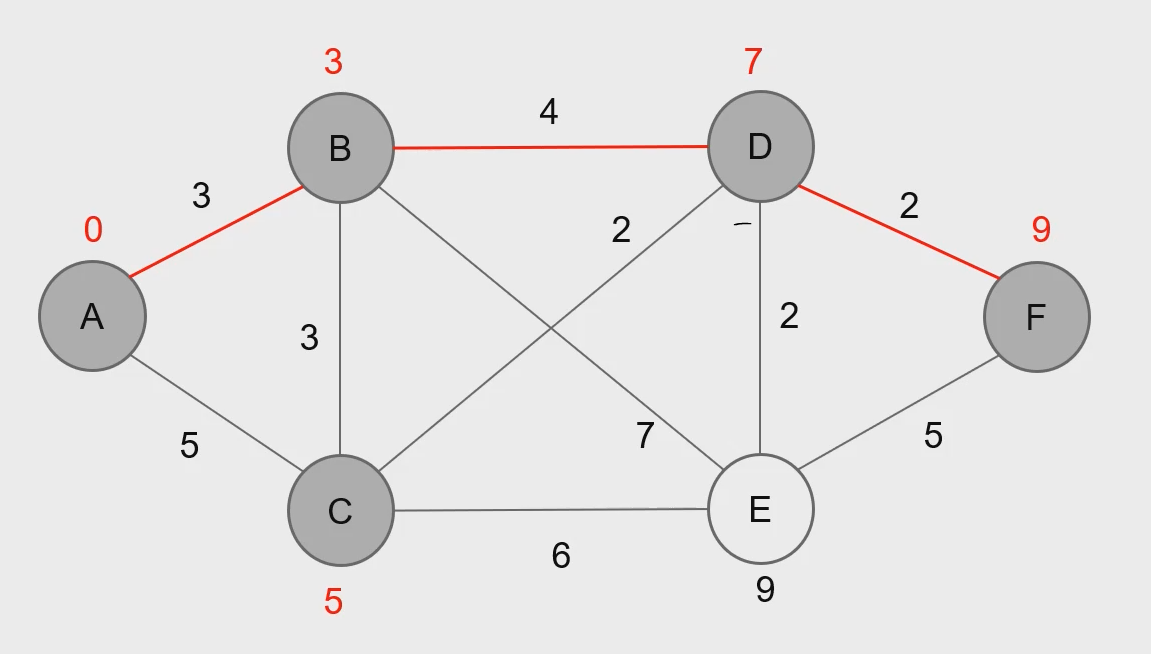
최단 경로문제의 정의 \- 입력 : G = (V,E,W), 시작 노드, 도착 노드 \- 출력 : 시작 노드부터 도착 노드까지의 최단 경로 \- 경로는 시작 노드부터 에지를 타고 계속 연결되어 도착노드까지 이르는 에지들의 집합 \- 경로의 가중치는 포함된 에지의
11.Bellman-Ford & Floyd-Warshall Algorithm

Bellman-Ford algorithm음의 가중치를 갖는 에지가 있을 때 사용하는 알고리즘 \- 다익스트라 알고리즘은 어ㅣㄷ에서 음의 가중치를 갖는 에지가 없다고 가정할까?왜 모든 에지에 같은 가중치를 더해줘서 음의 가중치인 에지를 없애면 안되는 걸까?경로마다 포함