Loss function
SVM - Hingle loss
xi = image, yi = label
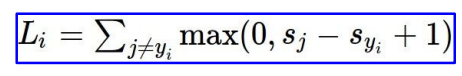
s_j = 잘못된 레이블의 스코어
s_yi = 제대로된 레이블의 스코어
각 로스들을 더해주고 클래스 개수로 나눠줌
Q) j = y_i 인 경우도 포함하여 모든 경우를 더해주면 무슨 일이 일어나는가
A) 각 결과값에 1이 더해질 것 → 평균값도 1만큼 증가
Q) 합 대신에 평균값 구하면 오때?
A) 큰 의미 없다.
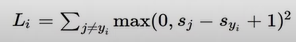
Q) 제곱한거 쓰면 어때?
A) non-linaer하기 때문에 차이가 생김
Q) max / min?
A) 무한대 / 0
Q) 일반적으로 W를 매우 작은 수로 초기화 → 처음에 score는 0에 가까운 값이 나옴.
이때 로스값은?
A) 2 (class 개수 -1 )
→ 최초 학습 시작할 때 로스값이 이 규칙에 맞는지 확인하면 학습이 제대로 시작되었는지를 확인할 수 있음.
Code

수식
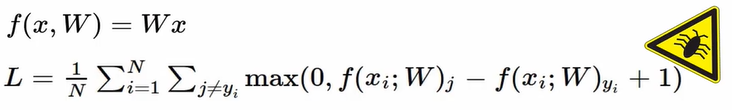
→ 버그 有
→ 로스를 0으로 만드는 Weight 파라미터값을 발견했다고 가정. 이 값이 유니크할까?
→ 유니크한 Weight 값을 만들기 위해서 “Weight Regularization”
Weight Regularization
w값이 얼마나 괜찮은가를 측정!
regularization loss: 테스트 셋쪽에 최대한 일반화하려고 노력 ←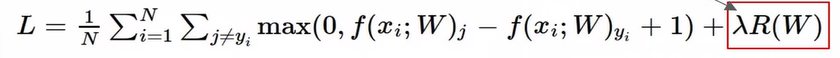
-------------------------------------------------
→ data loss : 학습용 데이터들에 최대한 최적화 하려고 노력이게 들어가게 되면 training 에러(training set 정확도 감소)는 더 커질 것/
But 결과물인 test dataset에 대한 정확도는 커짐!
Softmax Classifier
= multinomial Logistic Regression
제대로 된 클래스에 대한 로그의 확률을 최대화
= 정확한 클래스의 -로그 확률을 최소화 하자!

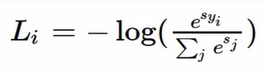
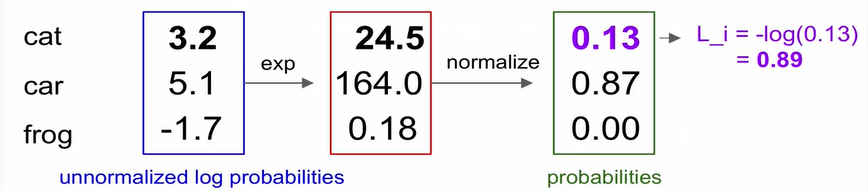
Q) min/max?
A) 0/ 무한대
Softmax vs SVM
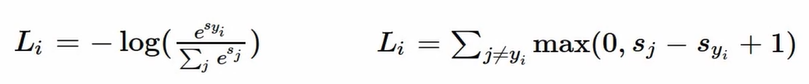
Q) 데이터의 스코어를 살짝씩 변형시켰을 때, 로스가 어떻게 바뀌는가?
A) - SVM) 로스값 불변 Softmax) 모든 인자값 고려하기 때문에 변화
→ SVM은 좀 둔간함. Softmax 민감해서 값 변화에 반응
Optimization
loss를 minimize 하는 weight 값을 찾아가는 과정!
산 속에서 호수를 찾기와 같음 → 경사를 따라 내려가자!
Gradient!
직접 계산해서 그래디언트 구함 = numerical gradient
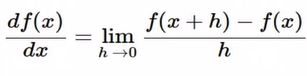
- 정확한 값X, 근사치!
- 계산속도 매우 느려영!
- 코드 작성은 쉬움~
Analytic gradient
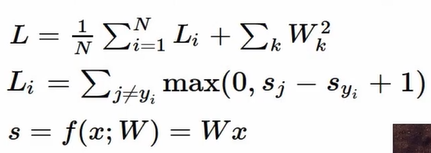
- loss는 기본적으로 weight function, 그냥 미분만 하면 ok
- 미분 통해서 구함!
- 정확하고
- 빠르다
- 코드 작성하게 되면 에러 발생 가능성 높아짐
→ 실제로는 언제나 analytic을 사용하되, 정확한지 확인하기 위해서 numerical을 사용!
Gradient Descent
음의 그래디언트 방향으로 움직이면서 최적화
실질적으로는 모두 탐색안하고 mini-batch! 일부만 활용해서 효율적으로 계산함
일반적으로 미니 배치 사이즈는 32/64/128
이 사이즈는 CPU, GPU에 적합한 사이즈로 하면 됨
running rate는 보통 높은 값 → 감소 시키면서 찾음
- feature 추출) 컬러 히스토그램 / HOG,SIFT/ Bag of Words
- 딥러닝에서는 피쳐 추출(사람이 인위적으로 해줬음) 안함. 알아서 함수 값 추출.

