[DL] 비전공자가 설명하는 CNN(Convolution Neural Networks) 개념

PhilAI·2023년 8월 25일

비전공자가 쉽게 알려주는 딥러닝 개념 👩‍🏫

목록 보기

2/2

📌 CNN이란?

CNN은 Convolution Neural Networks의 약자로 컴퓨터 비전 분야에서 이미지나 영상 데이터를 처리할 때 많이 이용됩니다. 모델을 이해할 때 해당 모델이 왜 생겨났는지에 대한 배경을 알아둔다면 모델을 이해하기 쉽습니다. 그렇다면 CNN을 왜 사용하게 된걸까요? 이건 MLP가 가진 한계점 때문입니다!

MLP(다층 퍼셉트론)은 이미지와 같은 2D 구조의 데이터를 평평하게 펼쳐서 처리할 수는 있지만, 이로 인해 이미지의 공간 구조와 지역적 정보가 손실될 수 있습니다. 이로 인해 이미지 내의 패턴, 텍스처, 공간적인 관계 등의 중요한 정보가 무시되며, 이로 인해 MLP를 사용한 학습은 이미지 처리 작업에 비효율적일 수 있습니다.

CNN은 이러한 문제를 극복하기 위해 등장한 모델입니다. CNN은 이미지를 input 그대로 받아서 공간적/지역적 정보를 보존하면서 특성의 계층을 구축하는데 중점을 둡니다. 이는 주로 두 가지 개념인 "합성곱 연산"과 "풀링"을 활용하여 이루어집니다.(뒤에서 상세하게 설명할께요 😀) CNN의 핵심 아이디어는 이미지를 작은 부분들로 나누어 보는 것이며, 이렇게 작은 부분을 통해 이미지의 지역적인 패턴과 특징을 감지하고 학습합니다. 이를 통해 이미지의 한 픽셀과 그 주변 픽셀들 간의 연관성을 살리고 이미지 내의 구조를 이해하는 데에 도움을 줍니다.

CNN 큰그림 이해하기

이해를 돕기 위해 간단한 예시로 다시 설명해보겠습니다!

이미지가 고양이인지 고양이가 아닌지를 감지하는 분류 모델을 구축한다고 가정해봅시다. 고양이와 다른동물(ex. 개, 곰, 사슴)/사물을 구분하기 위해서는 고양이라는 것을 특정할 수 있는 정보가 필요합니다. 이 경우에 눈,코,귀를 보면 고양이인지를 특정할 수 있다고 생각해봅시다.

하지만 세개의 정보는 전체 이미지에서 비교적 작은 부분을 차지 합니다. 따라서 전체 이미지를 다 보는 것보다 특정 부분을 잘라 중요 정보를 가지고 있는 지를 판별하는 것이 더 효율적일 것 입니다. 이를 해주는 것이 "CNN"입니다.

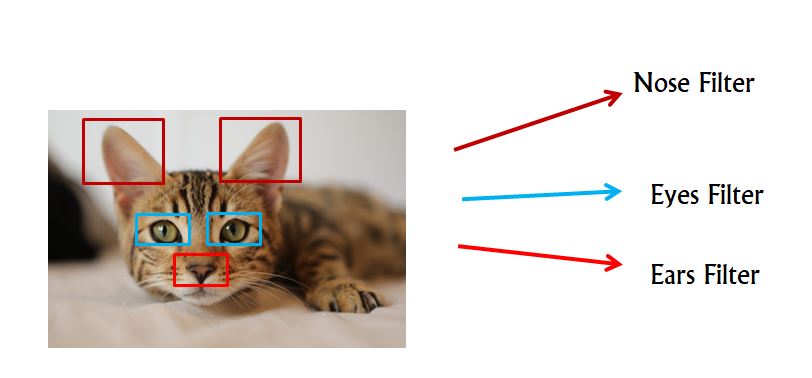
📌 CNN 작동원리

1️⃣ Convolution 이해하기

CNN은 Covolution Neutral Networks 약자이며 한국어로는 "합성곱 신경망"이라고 불립니다. 이때 Convolution/합성곱은 무슨 의미 일까요?

"convolution(합성곱)"은 신호 및 이미지 처리 뿐만 아니라 다양한 분야에서 사용되는 개념입니다만 CNN에서의 "convolution(합성곱)"은 이미지 처리와 패턴 인식을 위해 사용되는 기본 연산 중 하나입니다.

Convolution은 filter(kernel, feature detector)를 이미지와 겹쳐서 계산하는 작업을 말합니다. 이 때 filter는 이미지의 작은 부분에 적용되며, 각 부분에서 필터의 가중치와 이미지의 해당 부분의 값을 곱한 후 모두 더하여 결과를 얻어냅니다.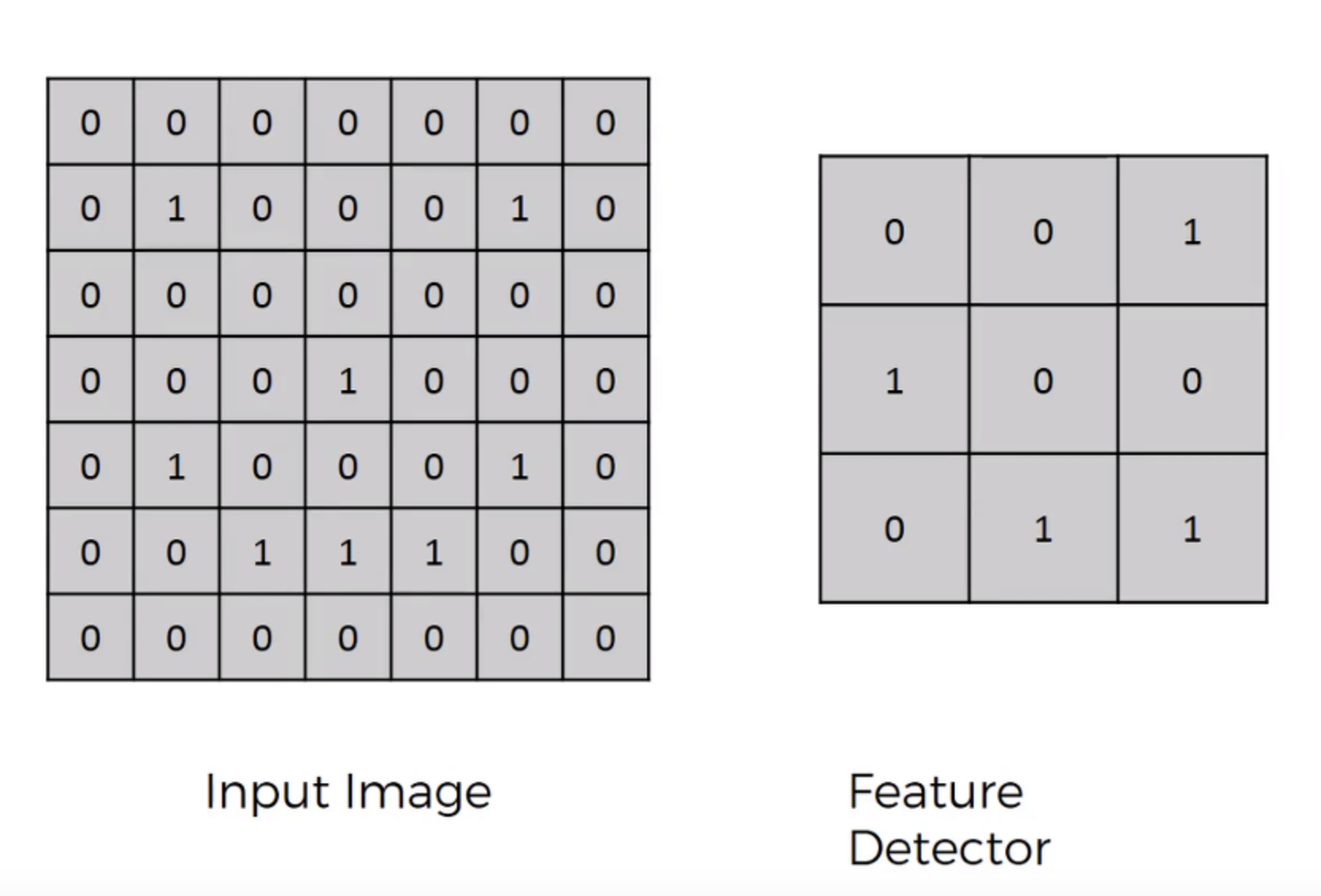

input 이미지과 feature detector이 주어졌습니다.(컴퓨터는 저희가 보는 이미지는 픽셀별로 변환하여 봅니다!) feature dectector은 input 이미지의 모든 영역을 훓으면서 주요 정보를 뽑게 됩니다. 주요 정보를 뽑은 결과값은 feature map으로 만들어 지게 됩니다.

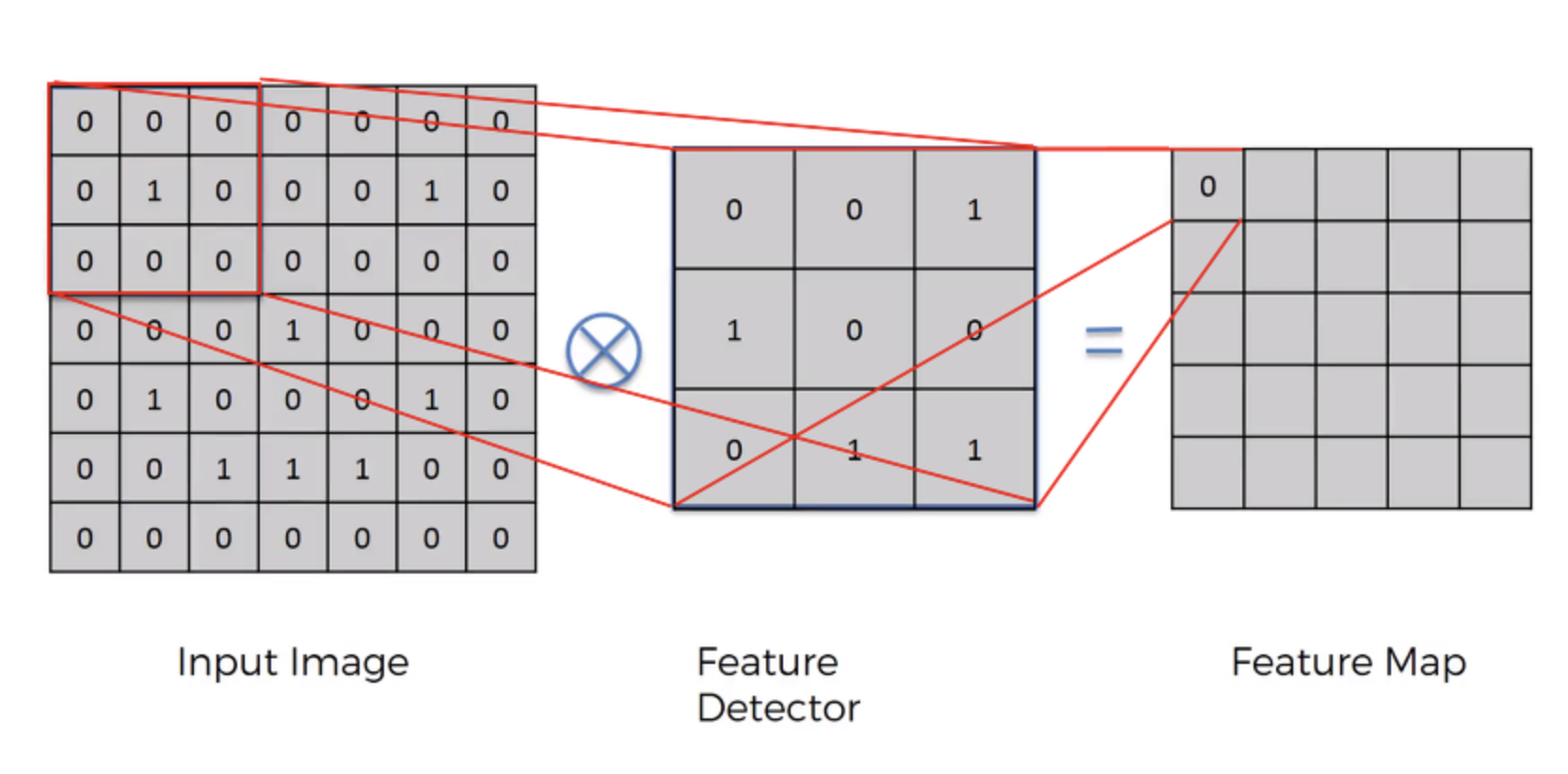
7x7 크기의 input 이미지에서 3x3 크기의 filter를 겹쳐서 움직이면서 연산을 수행하므로 (7-3+1) x (7-3+1) = 5x5 크기의 출력 이미지가 생성됩니다. 이때 출력 이미지의 크기가 입력 이미지보다 작아지는 현상이 발생합니다

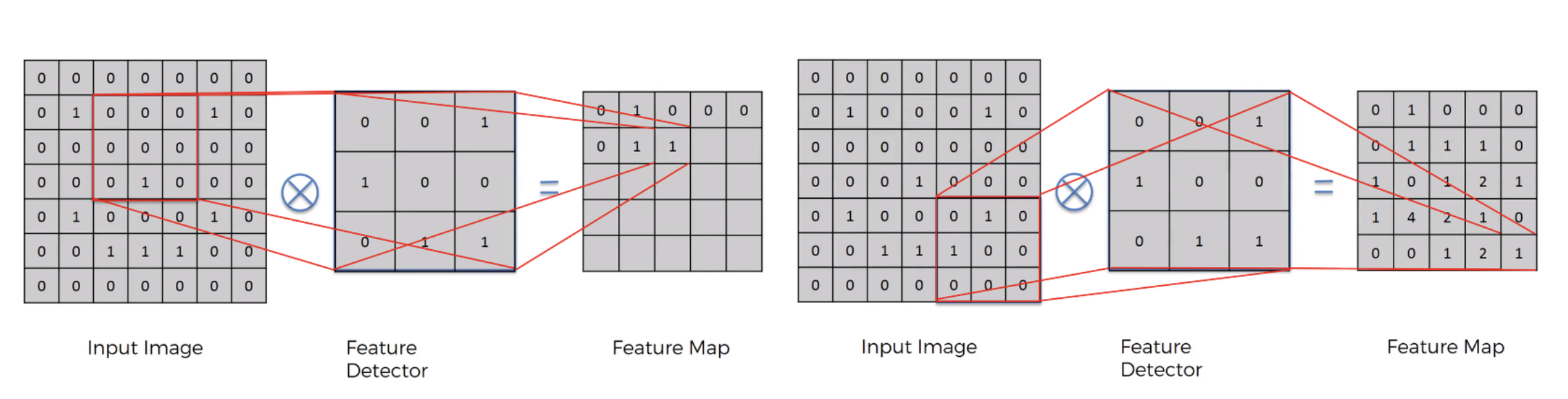
이미지가 작아진다는 것은 비교를 하는데 걸리는 속도가 빨라진 반면 데이터의 크기를 줄이면서 일부 미세한 디테일은 무시될 수 있습니다. 여기서 질문! 그러면 정보가 날아가면 고양이인지 판별못하는거 아닌가요?

결론적으로 말하면 정보 손실이 있어도 판별할 수 있다 입니다. 저희는 input 이미지의 모든 픽셀이 고양이 사진의 픽셀과 같은지를 판단하는 것이 아닌 input 이미지가 고양이의 특징을 가지고 있는지를 비교해야 합니다. 따라서 feature map에서 고양이의 귀/눈/코와 같은 패턴을 가졌는지를 확인하면 됩니다!

2️⃣ Stride

위에 예시에서는 필터를 오른쪽으로 한칸씩 옮겼습니다. 하지만 무조건 한칸씩 옮겨야 하는 것은 아닙니다. 여기서 나오는 개념이 "stride"입니다. 쉽게 말하면 stride는 filter가 얼마나 움직이는 것인가 입니다.
- Stride = 1

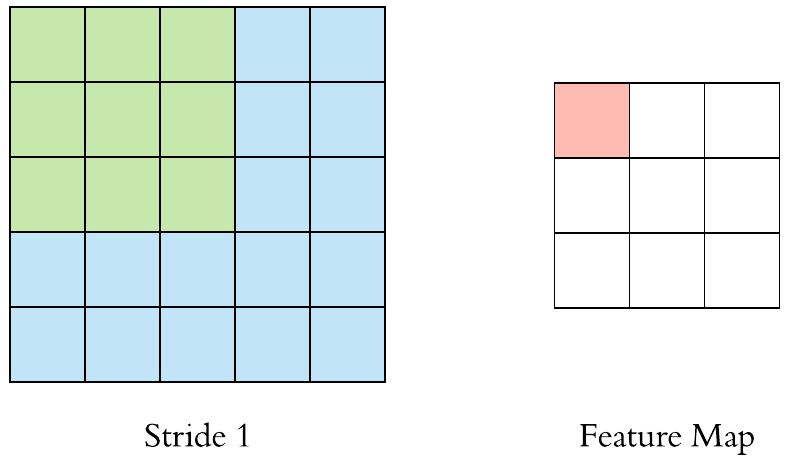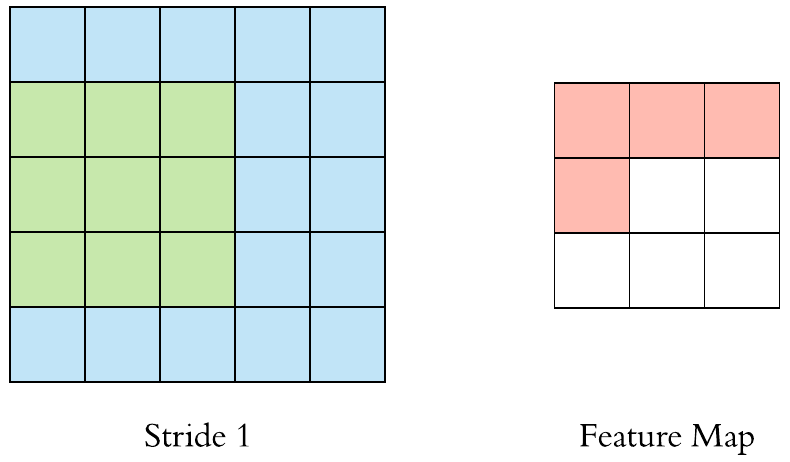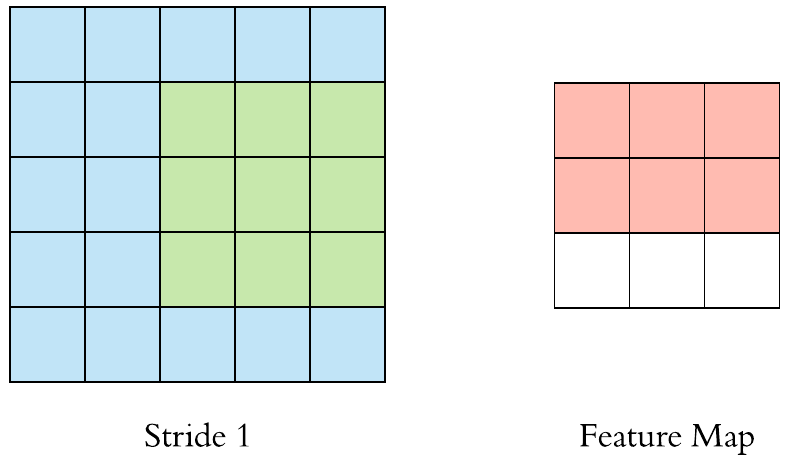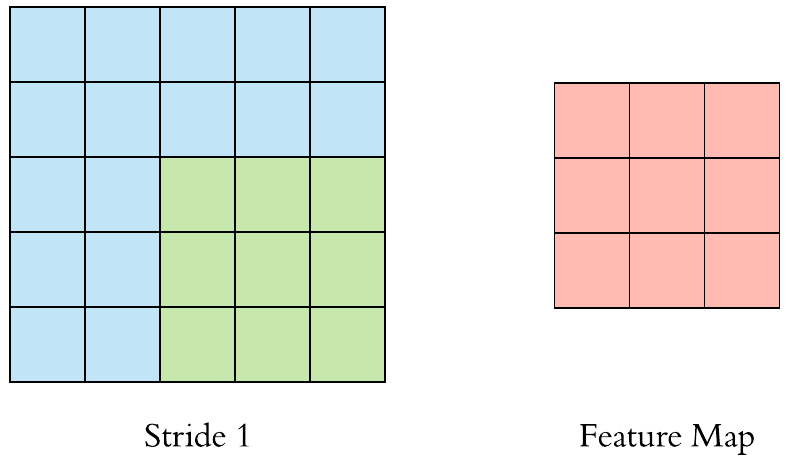
- Stride = 2

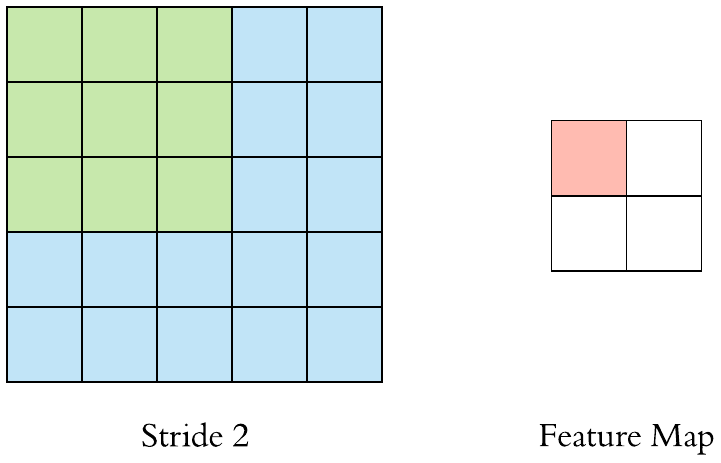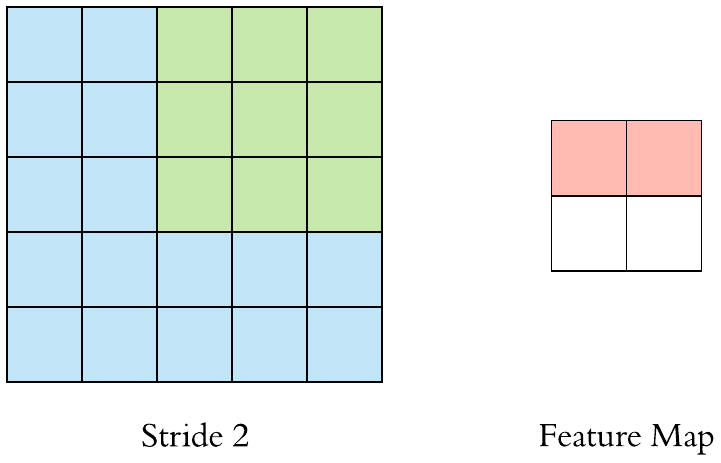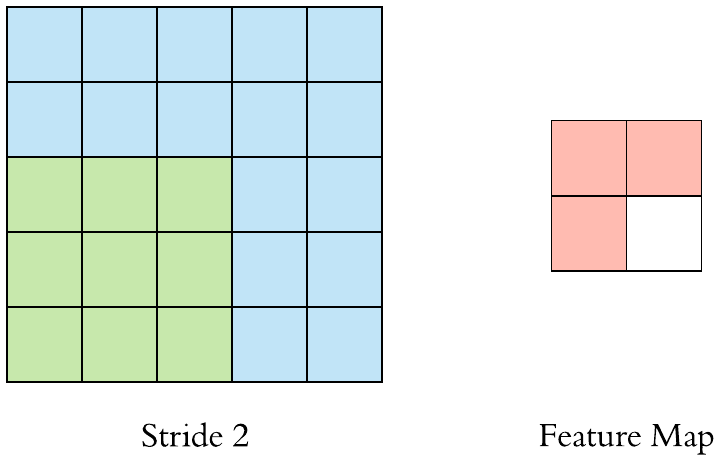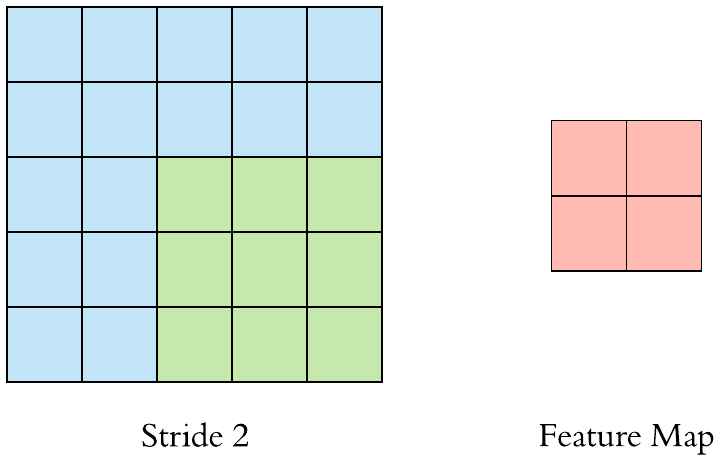
stride를 키우면 공간적인 feature 특성을 손실할 가능성이 높지만 불필요한 특성을 제거하는 효과와 Convolution 연산 속도를 향상시킵니다.

3️⃣ Padding

위에서 말했듯이 convolution을 반복하면 출력 사이즈가 줄어든다는 것을 확인했습니다. 이렇게 하다보면 가장자리 부분의 값은 합성곱을 하지 못하게 됩니다. 합성곱을 하지 못한다는 것은 가장자리의 정보를 잃어버린다는 것을 의미합니다.

이를 막기 위해서 "padding"이라는 개념이 들어오게 됩니다. 패딩 옷처럼 원래 몸보다 몸집을 키운다고 생각하시면 쉽습니다🧐 가장 많이 쓰는게 "zero padding"입니다. 0로 구성된 테두리를 이미지 가장자리에 감싸 준다고 생각하면 됩니다.

padding, stride 인해 output size가 달라지게 됩니다. output사이즈를 구하는 공식은 아래와 같으니 알아두시면 편할거에요 🙌
$(I - K + 2P)/S + 1)$ x $(I - K + 2P)/S + 1)$

I x I = 입력 사이즈

K x K = 필터 사이즈

P = 패딩 크기

S = strid 크기

📌 CNN 구조 알아보기

Convolution 작동원리에 대해 대략 감을 잡았다면 CNN 전체 구조에 대해 알아보도록 하겠습니다. 전체 구조는 아래의 그림과 같습니다!

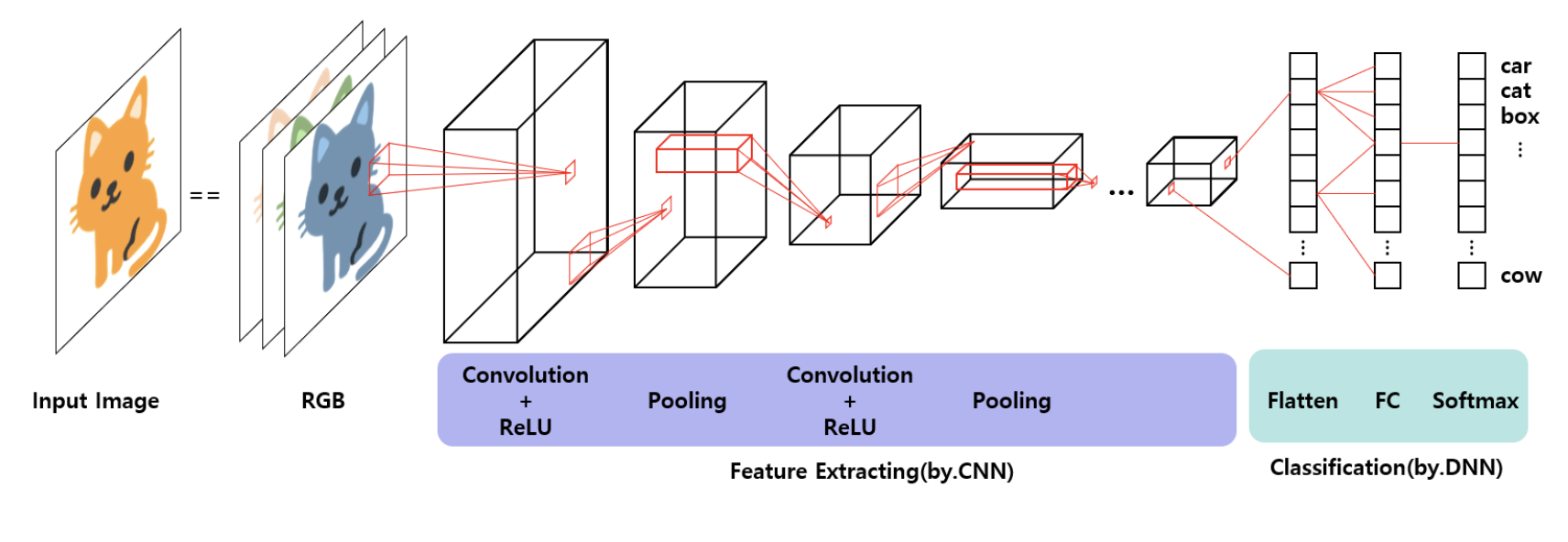
1️⃣ Convolution Layer: Convolution + ReLU

앞서 설명한 convolution과 활성화 함수 함께 사용한 것은 "convolution layer"라고 합니다. 주로 ReLU(Rectified Linear Activation) 함수가 사용됩니다.

convolution은 이해했는데 활성화 함수는 왜 쓸까?가 궁금할 겁니다🧐
선형함수(linear function)인 convolution에 비선형성을 추가하기 위해 사용하는 것입니다. (활성화 함수엔 대해서 별도의 글을 쓰도록 할께요!)

2️⃣ Pooling Layer

이전 단계의 합성곱(Convolution) 과정을 통해 다양한 특징 맵(feature map)이 생성되는데, 이러한 많은 특징 맵들을 그대로 다음 계층으로 넘겨주게 되면 매우 많은 계산이 필요해질 뿐만 아니라 모델의 파라미터 수도 급증하게 됩니다.

이를 위해 "풀링 레이어"개념이 들어오게 됩니다. 간략히 말하면, 풀링 레이어는 이미지에서 중요한 정보를 유지하면서 이미지 크기를 줄이는 역할을 합니다.
이렇게 해서 계산량을 줄이고 모델이 더 빠르고 효율적으로 작동하게 도와줍니다. 특히 이미지가 약간 움직여도 중요한 부분을 잘 인식할 수 있게 도와줍니다. 이렇게 함으로써 모델은 이미지의 특징을 더 정확하게 학습하고 분류하게 됩니다.

Pooling에는 대표적으로 두가지 방법으로 Max pooling과 Average pooling이 있습니다.

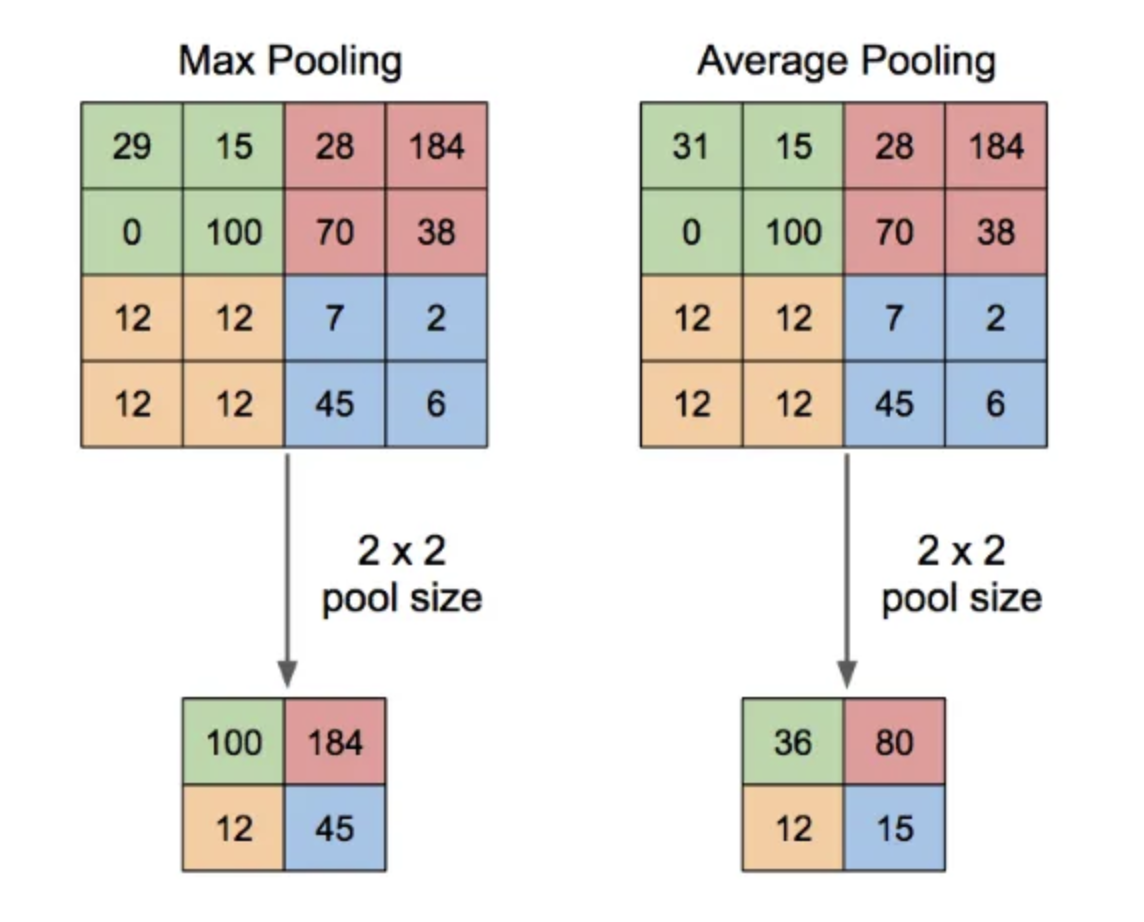
	Max Pooling	Average Pooling
장점	- 강한 특징을 감지할 수 있음	- 부드럽게 특징을 인식하고 노이즈를 줄임
	- 중요한 정보를 보존하며 불변성 유지	- 특징 분포의 평균을 계산하여 일반적인 특징 추출
단점	- 작은 변화에 민감할 수 있음	- 강한 특징을 놓칠 수 있음
	- 계산량이 더 많을 수 있음 (ReLU와 함께 사용 시)	- 모델이 세부 정보를 잃을 수 있음

"Convolution+Relu+Pooling"단계를 지나면서 input이미지는 점점 고차원으로 압축되어 계층적 특징을 잡아나가는 구조를 가지고 있습니다. 계층적 특징이란 아래의 그림처럼 점 -> 선 -> 물체 인식하는 것을 의미합니다.

3️⃣ Flatten

Flatten은 2차원 또는 다차원의 특징 맵(feature map)을 1차원 벡터로 변환하는 작업을 말합니다. 쉽게 말해 각 세로줄을 일렬로 줄 세우는 겁니다.

Flatten을 통해 1차원으로 변환된 데이터는 이미지의 공간적인 구조보다는 특징이나 패턴을 나타내는 데이터로써 활용됩니다. 특히 풀링 레이어에서 얻어낸 작은 크기의 특징 맵들은 이미지의 지역적인 정보보다는 주요 특징이나 패턴을 표현하는데 중점을 둡니다. 이러한 작은 특징 맵들을 1차원 벡터로 펼쳐서 완전 연결 레이어로 넘겨주는 것은 이러한 특징과 패턴을 모델이 더 잘 이해하고 활용할 수 있도록 도와주는 역할을 합니다.

정리하면, Flatten을 통해 얻어진 1차원 데이터는 이미지의 공간적인 구조보다는 주요 특징과 패턴을 표현하는 데이터로 변환된 것이며, 완전 연결 레이어에서 이러한 정보를 활용하여 모델이 패턴을 학습하고 판별하는 데 도움을 줍니다.

4️⃣ FC: Fully-Connected Layers(Dense Layers)

Fully-Connected Layers 또는 Dense Layers는 Convolutional Neural Network (CNN)의 마지막 부분에 있는 레이어입니다. 이 레이어는 이미지나 다른 입력 데이터의 추출된 특징을 기반으로 최종적인 결정을 내리는 역할을 합니다.

참고

PhilAI

철학과가 도전하는 Big Data, AI

이전 포스트