[자료구조] Array

📌 배열 (Array)

• Java에서 사이즈 구하기

int[] arr = { 1, 2, 3, 4, 5, 6, 7 };
int n = arr.length; // 7

배열 회전 프로그램

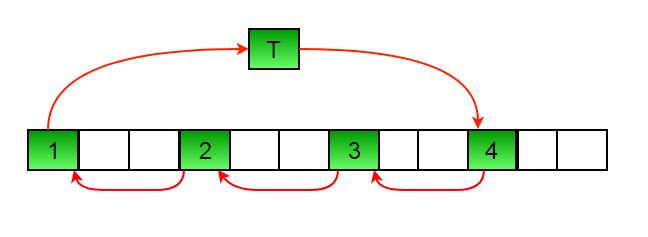
temp를 활용해서 첫번째 인덱스 값을 저장 후
arr[0]~arr[n-1]을 각각 arr[1]~arr[n]의 값을 주고, arr[n]에 temp를 넣어준다.

public static void leftRotatebyOne(int[] arr) {
    int n = arr.length; // 배열의 길이를 구함
    int temp = arr[0];  // 배열의 첫 번째 요소를 temp에 저장
    for(int i = 0; i < n - 1; i++) {
        arr[i] = arr[i+1]; // 배열의 요소들을 왼쪽으로 한 칸씩 이동
    }
    arr[n-1] = temp; // 마지막 요소에 temp 값을 대입
}

저글링 알고리즘

이 함수를 활용해 원하는 회전 수 만큼 for문을 돌려 구현이 가능

최대공약수 gcd를 이용해 집합을 나누어 여러 요소를 한꺼번에 이동시키는 것

위 그림처럼 배열이 아래와 같다면

arr[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}

1,2,3을 뒤로 옮길 때, 인덱스를 3개씩 묶고 회전시키는 방법이다.

a) arr [] -> { 4 2 3 7 5 6 10 8 9 1 11 12}

b) arr [] -> {4 5 3 7 8 6 10 11 9 1 2 12}

c) arr [] -> {4 5 6 7 8 9 10 11 12 1 2 3 }

public class JugglingAlgorithm {
  public static void leftRotate(int[] arr, int d) {
      int n = arr.length;
      int gcd = gcd(d, n); // 회전 횟수와 배열의 길이의 최대공약수를 구함

      for (int i = 0; i < gcd; i++) {
          int temp = arr[i];
          int j = i;
   
          while (true) {
              int k = j + d;

              if (k >= n) { // 배열의 범위를 넘어서면
                  k = k - n; // n만큼 빼서 배열의 처음으로 돌아옴
              }
              if (k == i) { // 시작점으로 돌아오면 종료
                  break;
              }
              arr[j] = arr[k];
              j = k; 
          }
          arr[j] = temp; // 마지막 요소에 temp 값을 대입
      }
  }

  // 최대공약수 계산
  private static int gcd(int a, int b) {
      if (b == 0) {
          return a;
      } else {
          return gcd(b, a % b);
      }
  }
}

역전 알고리즘

회전시키는 수에 대해 구간을 나누어 reverse로 구현하는 방법

d = 2이면

1,2 / 3,4,5,6,7로 구간을 나눈다.

첫번째 구간 reverse -> 2,1

두번째 구간 reverse -> 7,6,5,4,3

합치기 -> 2,1,7,6,5,4,3

합친 배열을 reverse -> 3,4,5,6,7,1,2

1 . Swap을 통한 Reverse:

public void reverseArr(int[] arr, int start, int end) {
  while (start < end) {
      int temp = arr[start]; // 두 값을 교환하기 위한 임시 변수
      arr[start] = arr[end];
      arr[end] = temp;

      start++; // 시작점을 오른쪽으로
      end--;   // 끝점을 왼쪽으로 이동
  }
}

2. 구간을 d로 나누었을 때 역전 알고리즘 구현:

public void rotateLeft(int[] arr, int d, int n) {
    reverseArr(arr, 0, d - 1);  // d 구간까지 reverse
    reverseArr(arr, d, n - 1);  // 나머지 구간 reverse
    reverseArr(arr, 0, n - 1);  // 전체 구간 reverse
}

📌 배열의 특정 최대 합 구하기

예시) arr[i]가 있을 때, i*arr[i]의 Sum이 가장 클 때 그 값을 출력하기

(회전하면서 최대값을 찾아야한다.)

Input: arr[] = {1, 20, 2, 10}
Output: 72

2번 회전했을 때 아래와 같이 최대값이 나오게 된다.
{2, 10, 1, 20}
20*3 + 1*2 + 10*1 + 2*0 = 72

Input: arr[] = {10, 1, 2, 3, 4, 5, 6, 7, 8, 9};
Output: 330

9번 회전했을 때 아래와 같이 최대값이 나오게 된다.
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
0*1 + 1*2 + 2*3 ... 9*10 = 330

접근 방법

arr[i]의 전체 합과 i*arr[i]의 전체 합을 저장할 변수 선언

최종 가장 큰 sum 값을 저장할 변수 선언

배열을 회전시키면서 i*arr[i]의 합의 값을 저장하고, 가장 큰 값을 저장해서 출력하면 된다.

해결법

회전 없이 i*arr[i]의 sum을 저장한 값
R0 = 0*arr[0] + 1*arr[1] +...+ (n-1)*arr[n-1]


1번 회전하고 i*arr[i]의 sum을 저장한 값
R1 = 0*arr[n-1] + 1*arr[0] +...+ (n-1)*arr[n-2]

이 두개를 빼면?
R1 - R0 = arr[0] + arr[1] + ... + arr[n-2] - (n-1)*arr[n-1]

2번 회전하고 i*arr[i]의 sum을 저장한 값
R2 = 0*arr[n-2] + 1*arr[n-1] +...+ (n?1)*arr[n-3]

1번 회전한 값과 빼면?
R2 - R1 = arr[0] + arr[1] + ... + arr[n-3] - (n-1)*arr[n-2] + arr[n-1]


여기서 규칙을 찾을 수 있음.

Rj - Rj-1 = arrSum - n * arr[n-j]

이를 활용해서 몇번 회전했을 때 최대값이 나오는 지 구할 수 있다.

코드

public static int maxSum(int[] arr) {
    int n = arr.length;
    int arrSum = 0;  
    int currVal = 0;

    // 배열의 전체 합과 i*arr[i] 값을 초기화
    for (int i = 0; i < n; i++) {
        arrSum += arr[i];
        currVal += i * arr[i];
    }

    int maxVal = currVal; // 최대값 초기화

    // 배열을 회전시키며 최대값 계산
    for (int j = 1; j < n; j++) {
        currVal = currVal + arrSum - n * arr[n-j];
        if (currVal > maxVal) {
            maxVal = currVal;
        }
    }
    return maxVal; // 최대값 반환
}

📌 특정 배열을 arr[i] = i로 재배열 하기

예시) 주어진 배열에서 arr[i] = i이 가능한 것만 재배열 시키기

Input : arr = {-1, -1, 6, 1, 9, 3, 2, -1, 4, -1}
Output : [-1, 1, 2, 3, 4, -1, 6, -1, -1, 9]

Input : arr = {19, 7, 0, 3, 18, 15, 12, 6, 1, 8,
              11, 10, 9, 5, 13, 16, 2, 14, 17, 4}
Output : [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 
         11, 12, 13, 14, 15, 16, 17, 18, 19]

arr[i] = i가 없으면 -1로 채운다.

접근 방법

arr[i]가 -1이 아니고, arr[i]이 i가 아닐 때가 우선 조건

해당 arr[i] 값을 저장(x)해두고, 이 값이 x일 때 arr[x]를 탐색

arr[x] 값을 저장(y)해두고, arr[x]가 -1이 아니면서 arr[x]가 x가 아닌 동안을 탐색

arr[x]를 x값으로 저장해주고, 기존의 x를 y로 수정

코드

public static void rearrange(int[] arr) {
    int n = arr.length;

    for (int i = 0; i < n; i++) {
        // arr[i]가 -1이 아니고 arr[i]가 i가 아니면
        if (arr[i] != -1 && arr[i] != i) {
            int x = arr[i]; // 현재 요소의 값 저장
            
            // x의 위치에 따라 재배열
            while (arr[x] != -1 && arr[x] != x) {
                int y = arr[x];
                arr[x] = x;
                x = y;
            }
            
            arr[x] = x; // x 위치에 x 값을 저장
            
            // arr[i]가 i 위치에 없으면 -1로 설정
            if (arr[i] != i) {
                arr[i] = -1;
            }
        }
    }
}