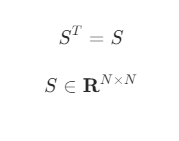[수학] 넘파이로 공부하는 선형대수 - 데이터와 행렬

데이터 사이언스 스쿨 수학편을 바탕으로 공부한 내용입니다.

---

선형대수

데이터의 유형

선형대수에서 다루는 데이터는 개수나 형태에 따라 크게 스칼라(scalar), 벡터(vector), 행렬(matrix), 텐서(tensor) 유형으로 나뉜다.

• 스칼라는 단 하나의 숫자로 이루어진 데이터를 나타냅니다.
• 벡터는 여러 숫자로 이루어진 데이터 레코드, 즉 데이터의 한 행을 나타냅니다.
• 행렬은 이러한 벡터, 즉 데이터 레코드가 여럿인 데이터 집합으로 구성됩니다.
• 텐서는 같은 크기의 여러 행렬이 모여 있는 데이터 구조로 생각할 수 있습니다.

예제에 사용할 데이터 : iris

from sklearn.datasets import load_iris  

iris = load_iris()  # 데이터 로드
iris.data[0, :]  # 첫 번째 꽃의 데이터

스칼라

스칼라는 하나의 숫자만으로 이루어진 데이터를 말한다.

스칼라는 보통 x와 같이 알파벳 소문자로 표기하며 실수(real number)인 숫자 중의 하나이므로 실수 집합 R의 원소라는 의미에서 다음처럼 표기한다.

$x ∈ R$

벡터

벡터는 여러 개의 숫자가 특정한 순서대로 모여 있는 것을 말한다.

예를 들어 붓꽃의 종을 알아내기 위해 붓꽃의 크기를 측정할 때, 꽃받침의 길이 x1뿐 아니라 꽃받침의 폭 x2, 꽃잎의 길이 x3, 꽃잎의 폭 x4라는 4개의 숫자를 측정할 수도 있다. 이런 데이터 묶음을 선형대수에서는 벡터라고 부른다.

붓꽃의 크기 벡터는 4개의 데이터 (x1,x2,x3,x4)가 하나로 묶여 있는데 이를 선형대수 기호로는 다음처럼 하나의 문자 x로 표기한다.

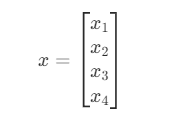
하나의 벡터를 이루는 데이터의 개수가 n개이면 이 벡터를 n-차원 벡터(n-dimensional vector)라고 하며 다음처럼 표기한다.

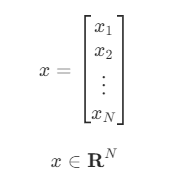
위에서 예로 든 붓꽃의 크기 벡터 x는 실수 4개로 이루어져 있으므로 4차원 벡터라고 하고 다음처럼 표기한다.

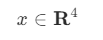
아래 첨자를 가진 알파벳 소문자 기호는 스칼라일 수도 있고 벡터일 수도 있다. 두 경우는 문맥에 따라 구별해야 한다. 책에 따라서는 벡터와 스칼라와 구별하기 위해 볼드체 벡터 기호 x나 화살표 벡터 기호 $\vec{x}$ 를 사용하기도 한다.

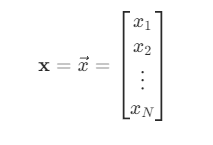
특징 벡터

데이터 벡터가 예측 문제에서 입력 데이터로 사용되면 특징 벡터(feature vector) 라고 한다.

넘파이를 사용한 벡터 표현

벡터의 차원은 원소 개수를 뜻한다. 배열은 원소 개수가 몇 개이든 한 줄로 나타낼 수 있다면 1차원 배열(1-dimensional array)이라고 한다.

원소를 가로와 세로가 있는 여러 줄의 직사각형 형태로 나타낼 수 있으면 2차원 배열(2-dimensional array)이라고 한다.`

# 2차원 배열
x1 = np.array([[5.1], [3.5], [1.4], [0.2]])
x1

array([[5.1],
       [3.5],
       [1.4],
       [0.2]])

# 넘파이는 1차원 배열 객체도 대부분 벡터로 인정한다
x1 = np.array([5.1, 3.5, 1.4, 0.2])
x1

array([5.1, 3.5, 1.4, 0.2])

사이킷런 패키지에서 벡터를 요구하는 경우에는 반드시 열의 개수가 1개인 2차원 배열 객체를 넣어야 한다.

연습 문제

숫자 이미지를 입력받아 어떤 숫자인지 분류하는 문제를 생각해보자. 이미지는 원래 2차원 데이터이지만 예측 문제에서는 보통 1차원 벡터로 변환하여 사용한다.

from sklearn.datasets import load_digits 

digits = load_digits()  # 데이터 로드
samples = [0, 10, 20, 30, 1, 11, 21, 31]  # 선택된 이미지 번호
d = []
for i in range(8):
    d.append(digits.images[samples[i]])

plt.figure(figsize=(8, 2))
for i in range(8):
    plt.subplot(1, 8, i + 1)
    plt.imshow(d[i], interpolation='nearest', cmap=plt.cm.bone_r)
    plt.grid(False); plt.xticks([]); plt.yticks([])
    plt.title("image {}".format(i + 1))
plt.suptitle("숫자 0과 1 이미지")
plt.tight_layout()
plt.show()

2차원 이미지를 64-크기의 1차원 벡터로 펼치면 다음과 같다.

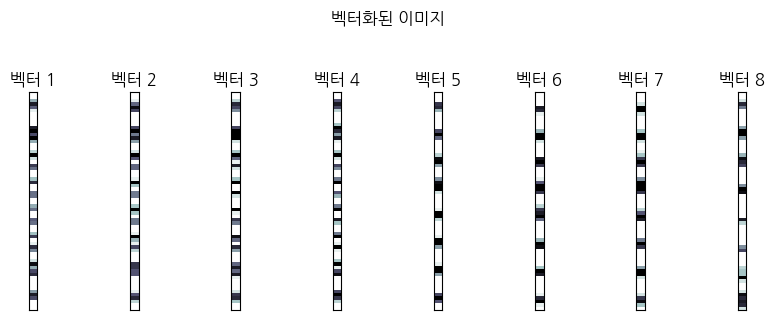
행렬

행렬은 복수의 차원을 가지는 데이터 레코드가 다시 여러 개 있는 경우의 데이터를 합쳐서 표기한 것이다.

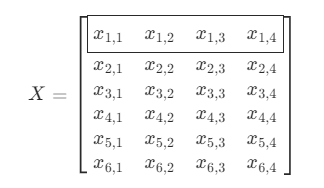
데이터를 행렬로 묶어서 표시할 때는 붓꽃 하나에 대한 데이터 레코드, 즉 하나의 벡터가 열이 아닌 행(row)으로 표시한다.

붓꽃의 예에서는 하나의 데이터 레코드가 4차원 데이터였다는 점을 기억하자.

하나의 데이터 레코드를 단독으로 벡터로 나타낼 때는 하나의 열(column) 로 나타내고 복수의 데이터 레코드 집합을 행렬로 나타낼 때는 하나의 데이터 레코드가 하나의 행(row) 으로 표기하는 것은 얼핏 보기에는 일관성이 없어 보지만 추후 다른 연산을 할 때 이런 모양이 필요하기 때문이다.

스칼라와 벡터도 수학적으로는 행렬에 속한다. 스칼라는 열과 행의 수가 각각 1인 행렬이고 벡터는 열의 수가 1인 행렬이다. 그래서 스칼라나 벡터의 크기를 표시할 때 다음처럼 쓸 수도 있다.

• 스칼라

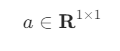
• 벡터
  

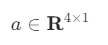
• 행렬
  

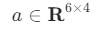
A = np.array([[11,12,13],[21,22,23]])
A

array([[11, 12, 13],
       [21, 22, 23]])

텐서

텐서는 같은 크기의 행렬이 여러 개 같이 묶여 있는 것을 말한다.

예를 들어 다음 컬러 이미지는 2차원의 행렬처럼 보이지만 사실 빨강, 초록, 파랑의 밝기를 나타내는 3가지의 이미지가 겹친 것이다.

컬러 이미지에서는 각각의 색을 나타내는 행렬을 채널(channel)이라고 한다.

예제 이미지는 크기가 768 x 1024이고 3개의 채널이 있으므로 768 x 1024 x 3 크기의 3차원 텐서다.

from scipy import misc  

img_rgb = misc.face()  
img_rgb.shape  

plt.subplot(221)
plt.imshow(img_rgb, cmap=plt.cm.gray)  # 컬러 이미지 출력
plt.axis("off")
plt.title("RGB 컬러 이미지")

plt.subplot(222)
plt.imshow(img_rgb[:, :, 0], cmap=plt.cm.gray)  # red 채널 출력
plt.axis("off")
plt.title("Red 채널")

plt.subplot(223)
plt.imshow(img_rgb[:, :, 1], cmap=plt.cm.gray)  # green 채널 출력
plt.axis("off")
plt.title("Green 채널")

plt.subplot(224)
plt.imshow(img_rgb[:, :, 2], cmap=plt.cm.gray)  # blue 채널 출력
plt.axis("off")
plt.title("Blue 채널")

plt.show()

전치 연산

전치(transpose) 연산은 행렬에서 가장 기본이 되는 연산으로 행렬의 행과 열을 바꾸는 연산을 말한다.

전치 연산은 벡터나 행렬에 T라는 위첨자(superscript)를 붙여서 표기한다.

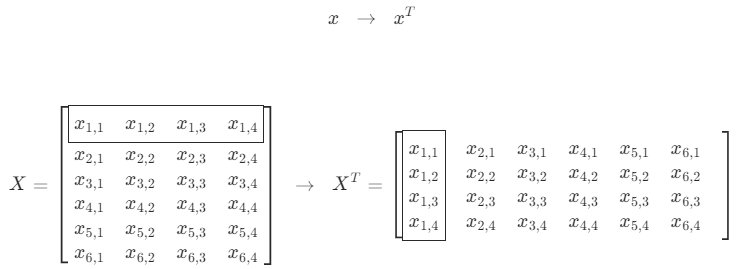
전치 연산으로 만든 행렬을 원래 행렬에 대한 전치행렬이라고 한다.

(열)벡터 x에 대해 전치 연산을 적용하여 만든 xT는 행의 수가 1인 행렬이므로 행 벡터(row vector) 라고 한다.

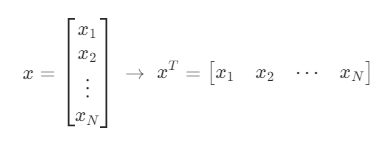
# NumPy에서는 ndarray 객체의 T라는 속성을 이용하여 전치 행렬을 구한다

print('A\n{}\n'.format(A))
print('A.T\n{}'.format(A.T))

A
[[11 12 13]
 [21 22 23]]

A.T
[[11 21]
 [12 22]
 [13 23]]

x1 = iris.data[0,:]
x1

array([5.1, 3.5, 1.4, 0.2])

#  1차원 ndarray는 전치 연산이 정의되지 않는다.
x1.T

array([5.1, 3.5, 1.4, 0.2])

연습 문제

NumPy를 사용해서 붓꽃 데이터 X의 전치행렬 XT을 구한다.

X = iris.data
print(X.shape)
X[:30]

(150, 4)
array([[5.1, 3.5, 1.4, 0.2],
       [4.9, 3. , 1.4, 0.2],
       [4.7, 3.2, 1.3, 0.2],
       [4.6, 3.1, 1.5, 0.2],
       [5. , 3.6, 1.4, 0.2],
       [5.4, 3.9, 1.7, 0.4],
       [4.6, 3.4, 1.4, 0.3],
       [5. , 3.4, 1.5, 0.2],
       [4.4, 2.9, 1.4, 0.2],
       [4.9, 3.1, 1.5, 0.1],
       [5.4, 3.7, 1.5, 0.2],
       [4.8, 3.4, 1.6, 0.2],
       [4.8, 3. , 1.4, 0.1],
       [4.3, 3. , 1.1, 0.1],
       [5.8, 4. , 1.2, 0.2],
       [5.7, 4.4, 1.5, 0.4],
       [5.4, 3.9, 1.3, 0.4],
       [5.1, 3.5, 1.4, 0.3],
       [5.7, 3.8, 1.7, 0.3],
       [5.1, 3.8, 1.5, 0.3],
       [5.4, 3.4, 1.7, 0.2],
       [5.1, 3.7, 1.5, 0.4],
       [4.6, 3.6, 1. , 0.2],
       [5.1, 3.3, 1.7, 0.5],
       [4.8, 3.4, 1.9, 0.2],
       [5. , 3. , 1.6, 0.2],
       [5. , 3.4, 1.6, 0.4],
       [5.2, 3.5, 1.5, 0.2],
       [5.2, 3.4, 1.4, 0.2],
       [4.7, 3.2, 1.6, 0.2]])

print(X.T.shape)
X.T[:1]

(4, 150)
array([[5.1, 4.9, 4.7, 4.6, 5. , 5.4, 4.6, 5. , 4.4, 4.9, 5.4, 4.8, 4.8,
        4.3, 5.8, 5.7, 5.4, 5.1, 5.7, 5.1, 5.4, 5.1, 4.6, 5.1, 4.8, 5. ,
        5. , 5.2, 5.2, 4.7, 4.8, 5.4, 5.2, 5.5, 4.9, 5. , 5.5, 4.9, 4.4,
        5.1, 5. , 4.5, 4.4, 5. , 5.1, 4.8, 5.1, 4.6, 5.3, 5. , 7. , 6.4,
        6.9, 5.5, 6.5, 5.7, 6.3, 4.9, 6.6, 5.2, 5. , 5.9, 6. , 6.1, 5.6,
        6.7, 5.6, 5.8, 6.2, 5.6, 5.9, 6.1, 6.3, 6.1, 6.4, 6.6, 6.8, 6.7,
        6. , 5.7, 5.5, 5.5, 5.8, 6. , 5.4, 6. , 6.7, 6.3, 5.6, 5.5, 5.5,
        6.1, 5.8, 5. , 5.6, 5.7, 5.7, 6.2, 5.1, 5.7, 6.3, 5.8, 7.1, 6.3,
        6.5, 7.6, 4.9, 7.3, 6.7, 7.2, 6.5, 6.4, 6.8, 5.7, 5.8, 6.4, 6.5,
        7.7, 7.7, 6. , 6.9, 5.6, 7.7, 6.3, 6.7, 7.2, 6.2, 6.1, 6.4, 7.2,
        7.4, 7.9, 6.4, 6.3, 6.1, 7.7, 6.3, 6.4, 6. , 6.9, 6.7, 6.9, 5.8,
        6.8, 6.7, 6.7, 6.3, 6.5, 6.2, 5.9]])

NumPy를 사용해서 위 전치행렬을 다시 전치한 행렬 (XT)T을 구한다. 이 행렬과 원래 행렬 X을 비교한다.

print(X.T.T.shape)
X.T.T[:30]

(150, 4)
array([[5.1, 3.5, 1.4, 0.2],
       [4.9, 3. , 1.4, 0.2],
       [4.7, 3.2, 1.3, 0.2],
       [4.6, 3.1, 1.5, 0.2],
       [5. , 3.6, 1.4, 0.2],
       [5.4, 3.9, 1.7, 0.4],
       [4.6, 3.4, 1.4, 0.3],
       [5. , 3.4, 1.5, 0.2],
       [4.4, 2.9, 1.4, 0.2],
       [4.9, 3.1, 1.5, 0.1],
       [5.4, 3.7, 1.5, 0.2],
       [4.8, 3.4, 1.6, 0.2],
       [4.8, 3. , 1.4, 0.1],
       [4.3, 3. , 1.1, 0.1],
       [5.8, 4. , 1.2, 0.2],
       [5.7, 4.4, 1.5, 0.4],
       [5.4, 3.9, 1.3, 0.4],
       [5.1, 3.5, 1.4, 0.3],
       [5.7, 3.8, 1.7, 0.3],
       [5.1, 3.8, 1.5, 0.3],
       [5.4, 3.4, 1.7, 0.2],
       [5.1, 3.7, 1.5, 0.4],
       [4.6, 3.6, 1. , 0.2],
       [5.1, 3.3, 1.7, 0.5],
       [4.8, 3.4, 1.9, 0.2],
       [5. , 3. , 1.6, 0.2],
       [5. , 3.4, 1.6, 0.4],
       [5.2, 3.5, 1.5, 0.2],
       [5.2, 3.4, 1.4, 0.2],
       [4.7, 3.2, 1.6, 0.2]])

행렬의 행 표기법과 열 표기법

행렬을 복수의 열 벡터 ci, 또는 복수의 행 벡터 rTj을 합친(concatenated) 형태로 표기할 수도 있다.

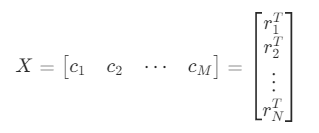
위 식에서 행렬과 벡터의 크기는 다음과 같다.

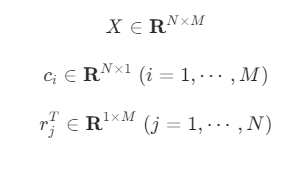
모든 벡터는 기본적으로 열벡터이므로 $r_i$를 전치 연산하여 $r_i^T$ 라고 행을 표현한 점에 주의한다.

특수한 벡터와 행렬

영벡터

모든 원소가 0인 N차원 벡터는 영벡터(zeros-vector) 라고 하며 다음처럼 표기한다.

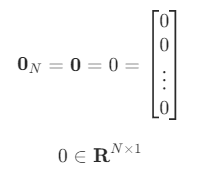
np.zeros((3,1))

array([[0.],
       [0.],
       [0.]])

일벡터

모든 원소가 0인 N
차원 벡터는 영벡터(zeros-vector) 라고 하며 다음처럼 표기한다.

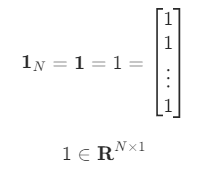
np.ones((3,1))

array([[1.],
       [1.],
       [1.]])

정방행렬

행의 개수와 열의 개수가 같은 행렬을 정방행렬(square matrix) 이라고 한다.

대각행렬

행렬에서 행과 열이 같은 위치를 주 대각(main diagonal) 또는 간단히 대각(diagonal) 이라고 한다.

대각 위치에 있지 않은 것들은 비대각(off-diagonal) 이라고 한다. 모든 비대각 요소가 0인 행렬을 대각행렬(diagonal matrix) 이라고 한다.

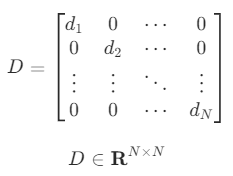
대각행렬이 되려면 비대각성분이 0이기만 하면 되고 대각성분은 0이든 아니든 상관없다.

또한 반드시 정방행렬일 필요도 없다

위의 행렬도 대각행렬이라고 할 수 있다.

np.diag([1,2,3])

array([[1, 0, 0],
       [0, 2, 0],
       [0, 0, 3]])

항등행렬

대각행렬 중에서도 모든 대각성분의 값이 1인 대각행렬을 항등행렬(identity matrix) 이라고 한다.

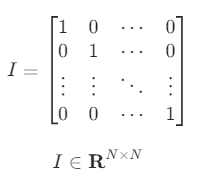
np.identity(3)

array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

      
np.eye(4)

array([[1., 0., 0., 0.],
       [0., 1., 0., 0.],
       [0., 0., 1., 0.],
       [0., 0., 0., 1.]])
       

대칭행렬

전치행렬과 원래의 행렬이 같으면 대칭행렬(symmetric matrix) 이라고 한다

정방행렬만 대칭행렬이 될 수 있다.