
📒 다익스트라(Dijkstra)가 뭔데?
📌 차례
- 정의
- 알고리즘의 이해(1) - 내가 알고리즘을 이해한 흐름
- 알고리즘의 이해(2) - 다익스트라(Dijkstra) 알고리즘
- 필요한 자료구조
- 핵심 알고리즘
📌 정의
가중치가 "양수"인 그래프에서의 "출발지"가 정해져있을 때, 해당 출발지에서 다른 모든 도착지들까지의 최단거리
여기서 "최단거리"라는 뜻은 특정 출발지에서 다른 도착지까지 가는 경로에 있는 모든 가중치의 합이 최소인 것을 의미한다.
📌 알고리즘의 이해(1) - 내가 알고리즘을 이해한 흐름
저는 예시를 먼저 보고 혼자 생각하는 시간을 가져보았어요.
제가 생각하는 스타일은,
먼저 이 문제가 일반적인 시험문제라고 생각하고 접근합니다.(전혀 컴퓨터에 대한 고려는 하지 않아요.🧠)
문제를 머리로 해결하면, 그 다음에 다시 한 번 복기해보면서 그때 제가 머리에서 어떤 생각의 흐름이 지나왔는지 되새겨봅니다!
이후 컴퓨터에 맞게 생각을 바꾼다기 보다, 그냥 일반화시킬 수 있는 규칙을 생성한다는 느낌으로 접근을 해보았습니다!
먼저 예시를 보여드릴게요!
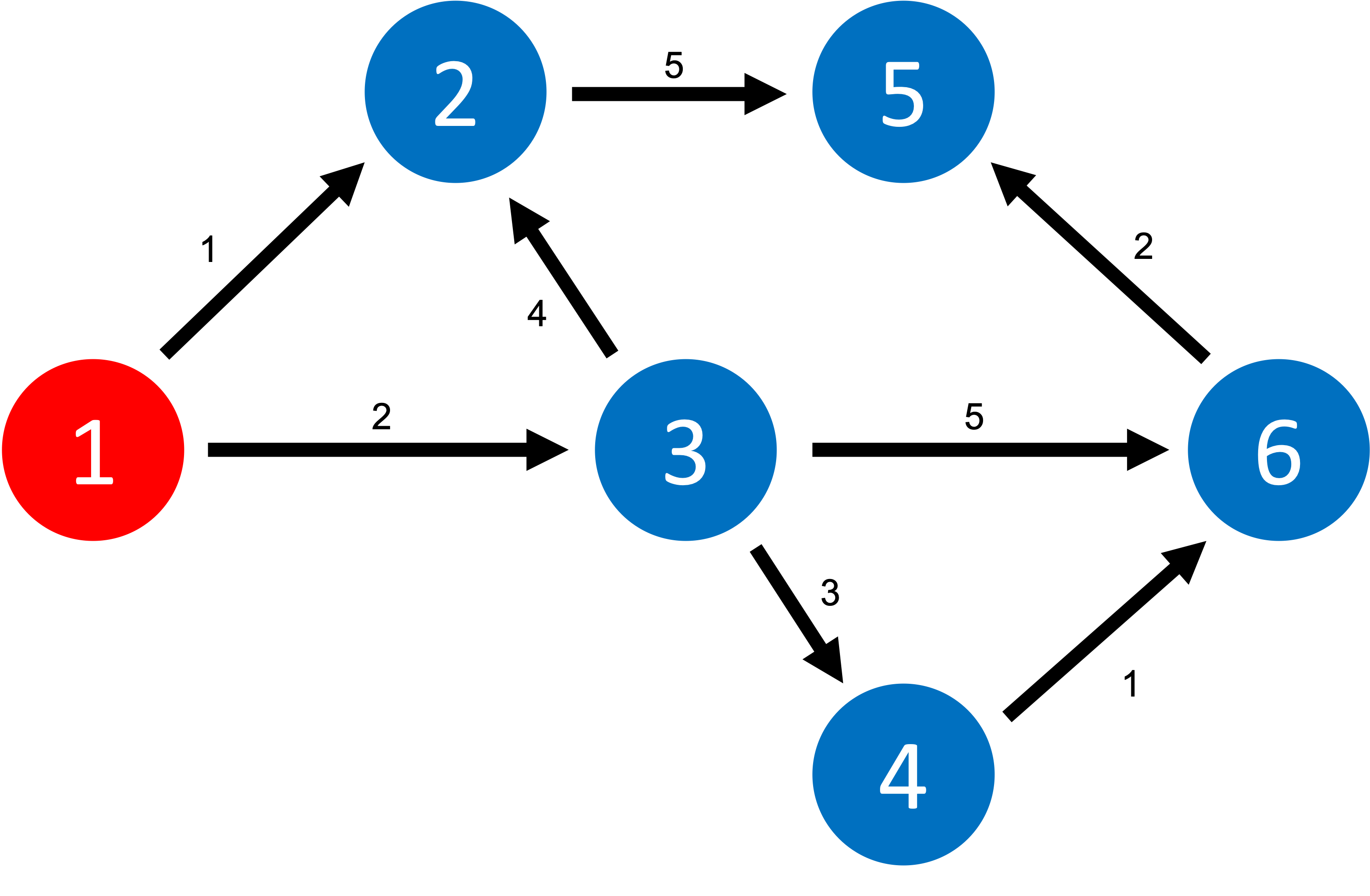
위의 그림을 보시고 먼저 문제를 푼다 생각하고 1번 출발지에서 각각의 도착지로 갈 때, 최솟값을 구해봅시다.✍️
같이 해볼까요??
우선 저는 가장 가중치가 작은, 가중치가 1인 1에서 2로가는 것을 먼저 선택했어요.
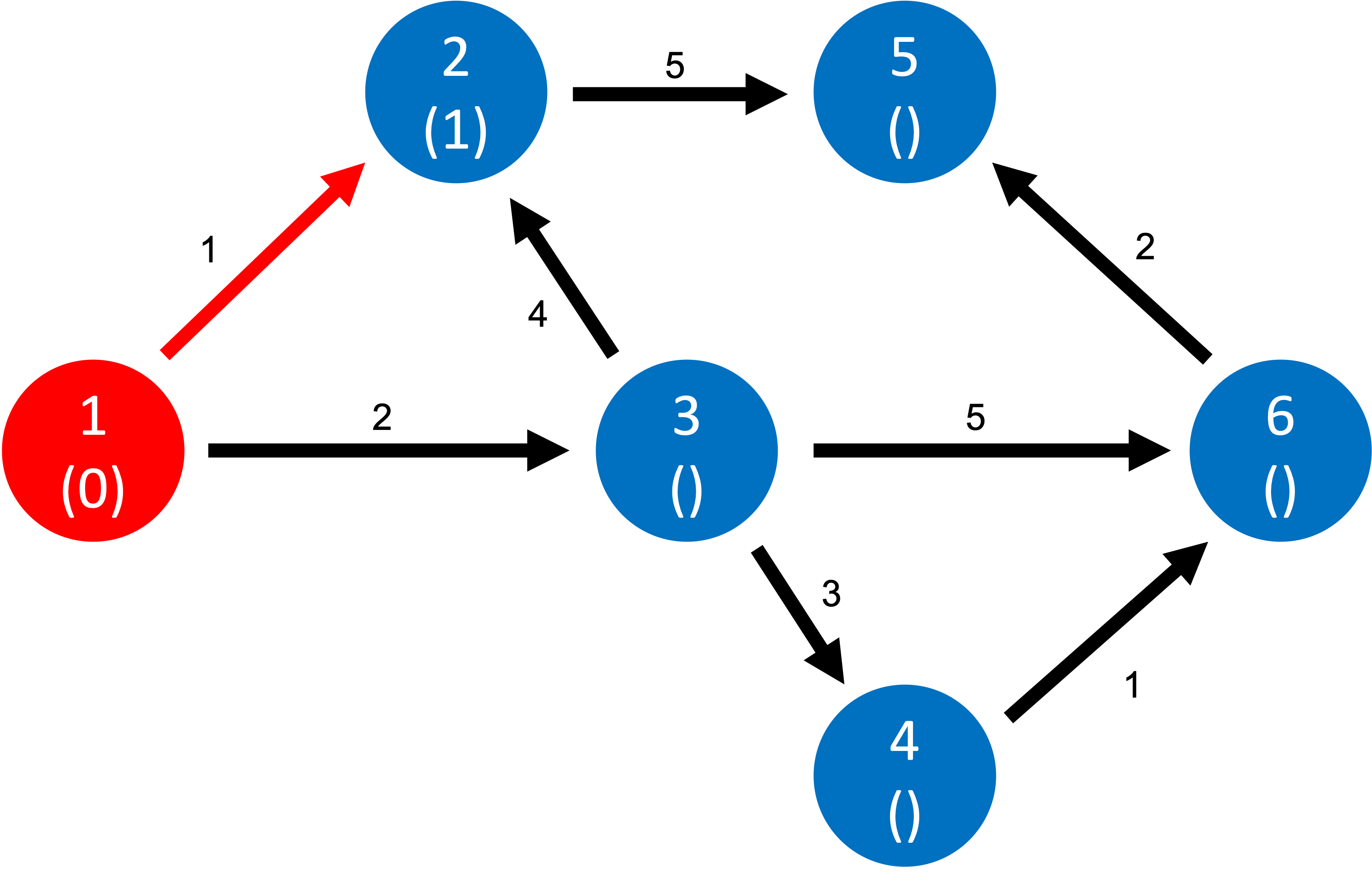
다음으로 가중치가 작은, 가중치가 2인 1에서 3으로 가는 것을 선택했습니다!
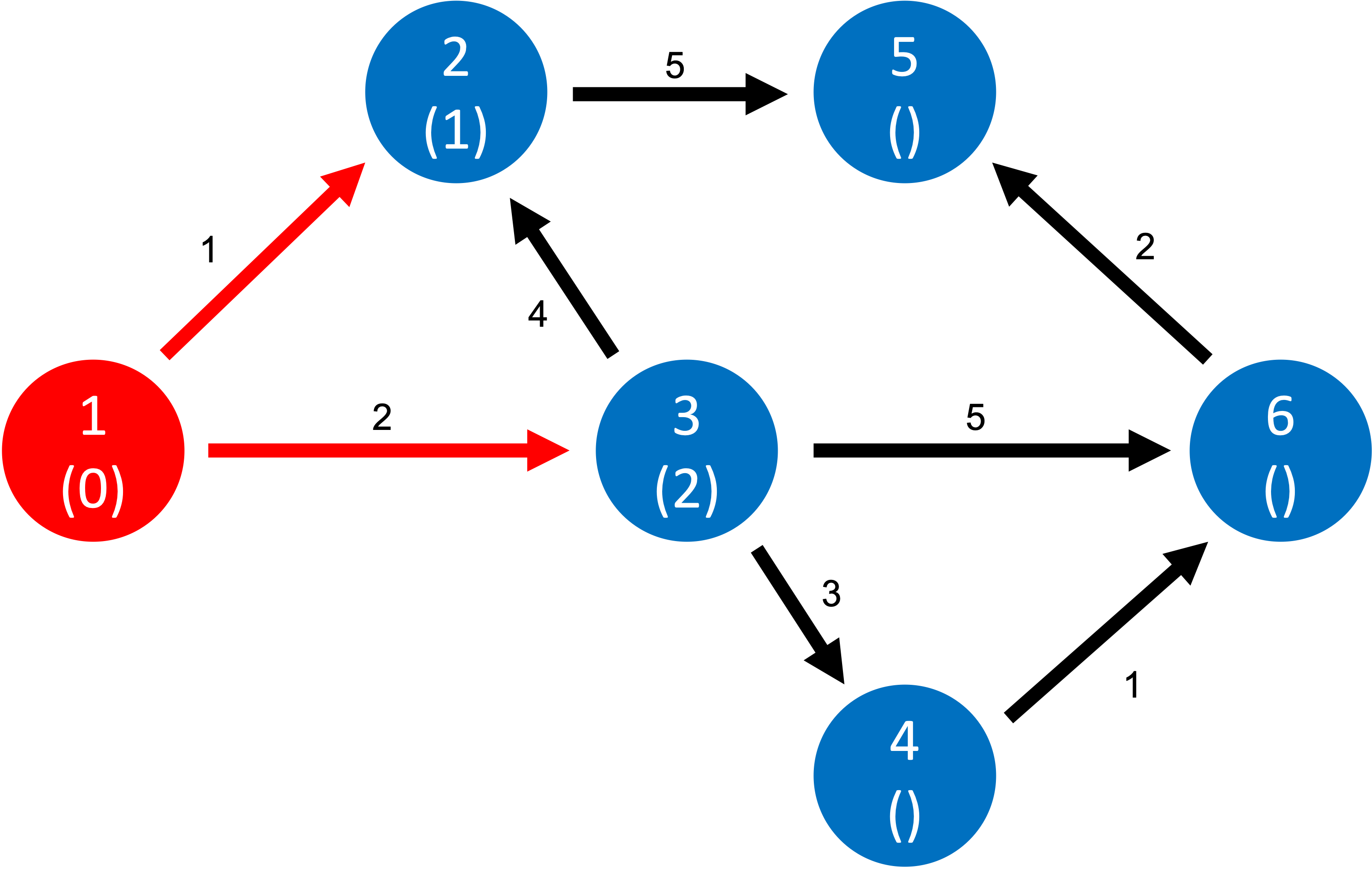
이렇게 처음 두개의 목적지를 가보면서 하나의 전략을 세웠는데요, 제가 생각한 전략은 가중치가 작은 간선들부터 차례대로 해보는 것이었습니다. (물론 이게 다익스트라는 전혀 아니죠😅)
이 전략으로 진행하다 보면, [ 2 > 3 > 4 > 6 > 5 ] 이 순서로 목적지를 도착하게 되는데요, 이 때의 5번 목적지를 가는 경로는 [ 1 > 3 > 4 > 6 > 5 ] 번이 됩니다. 가중치를 모두 더하면 8 ( = 2 + 3 + 1 + 2 )인걸 알수 있죠.
그치만 여러분들이 풀어보셔서 아시겠지만 5번 목적지의 최단거리는 6이죠. 1번에서 2번, 2번에서 5번으로 가면되니까요.
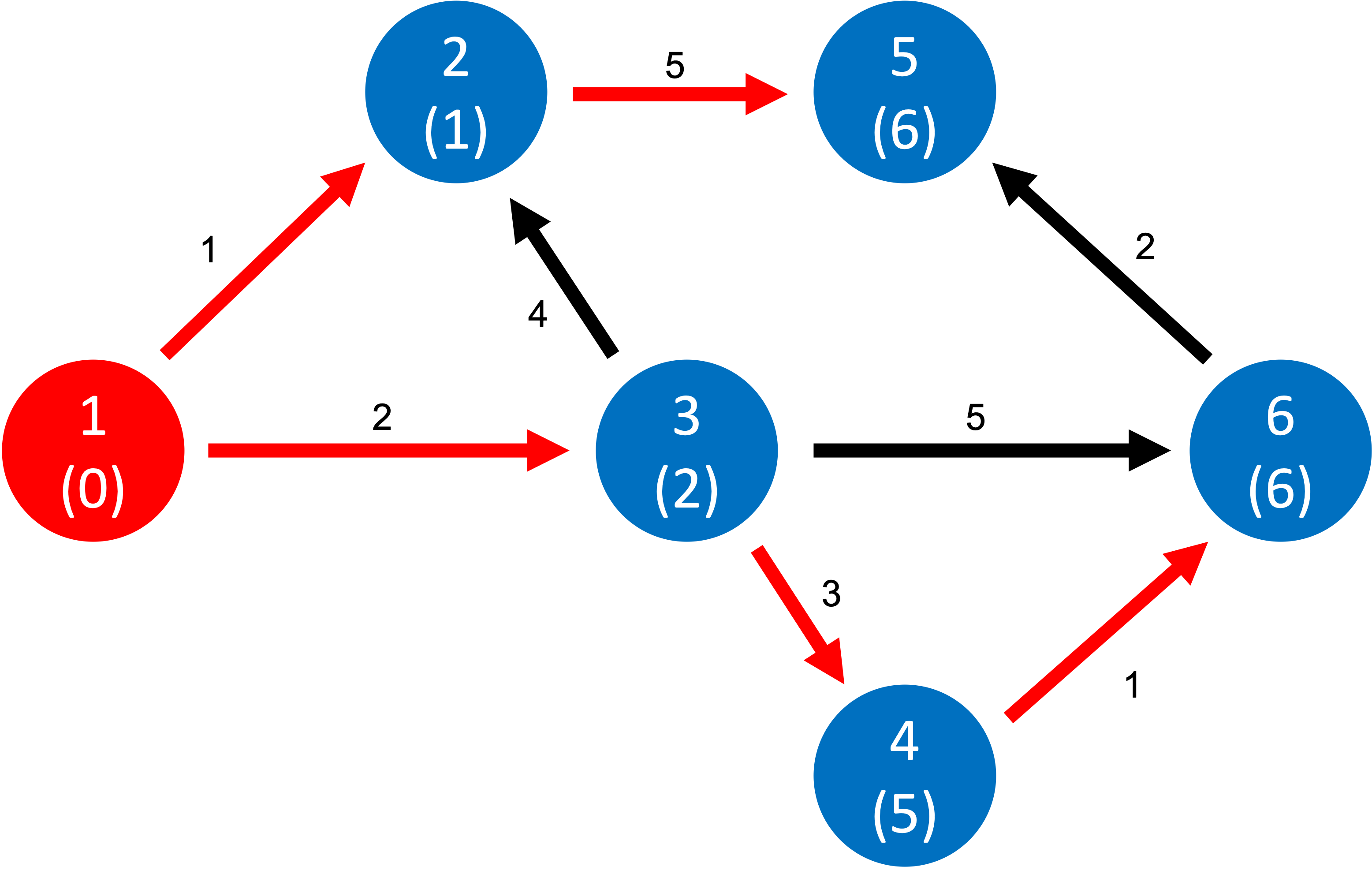
그래서 전략을 바꿔야 했습니다.
어떤게 좋을까요? (진짜로 한번 고민해보시는걸 추천합니다! 제가 고민해서 생각해보니까 절대로 잊어버리지 않아요!!)
📌 알고리즘의 이해(2) - 다익스트라(Dijkstra) 알고리즘
위에서 한번 고민해 보셨죠?? 🧐
이제 고민해보신게 맞는지 확인해봅시다!
< 다익스트라 알고리즘 >
- 모든 노드(NODE)* 중에서 현재 최단거리값이 가장 작은 노드를 선택합니다.(현재노드)
- 현재노드에서 방문할 수 있는 모든 노드를 찾습니다.
- 현재 노드에 최단거리값에 가중치를 더한 값과, 기존에 방문 가능한 노드에 저장되어있는 최단거리값을 비교합니다.
- 현재 노드에 최단거리값에 가중치를 더한 값이 더 작다면! 방문 가능한 노드에 저장되어있는 최단거리를 갱신합니다.
[ 반복 .......]
*NODE : 출발지, 도착지 등 방문하는 지점.
이해하기 좀 쉽지않네요. 그죠? 그래서 아까 예시와 함께 보겠습니다!
우선, 1번을 보시면 모든 노드중에서 최단거리값이 가장 작은 노드를 선택하는 것인데요. 현재 다른 모든 노드의 최단거리값은 채워져있지 않고, 빨간색 1번 노드만 0인 것을 알 수 있습니다. 그래서 현재노드는 1번(빨강노드)입니다.
그리고 2번을 보시면 현재노드에서 방문할 수 있는 모든 노드를 찾는다고 되어있습니다. 이전 예시에서 현재 노드는 빨강색이겠죠! 그리고 방문가능한 노드는 화살표가 가리키는 2,3번이 있을 겁니다.
그럼 3,4번 항목에 해당하는 (현재 노드 최단거리 + 가중치) 와 (방문 가능 노드의 최단거리) 를 비교해 봅시다.
현재 방문 가능 노드인 2,3번 노드에 아무것도 없으니까 당연히 (현재 노드 최단거리 + 가중치) 로 갱신을 해줘야 합니다.
처음은 쉽게 끝냈네요. 그쵸?
그러면 이제 한번 탐색을 끝낸 1번(빨간색)말고, 그 다음으로 최단거리값이 작은 것을 선택해 봅시다!
2번이 최단거리값이 1으로 3번의 2보다 작은것을 알 수 있습니다. 그러면 현재노드는 2번인 상태로 다시 위의 과정을 반복해봅시다. 2번에서는 방문가능한 노드가 5번 밖에 없네요. 그러면 5번은 갱신하여 6이 됩니다.
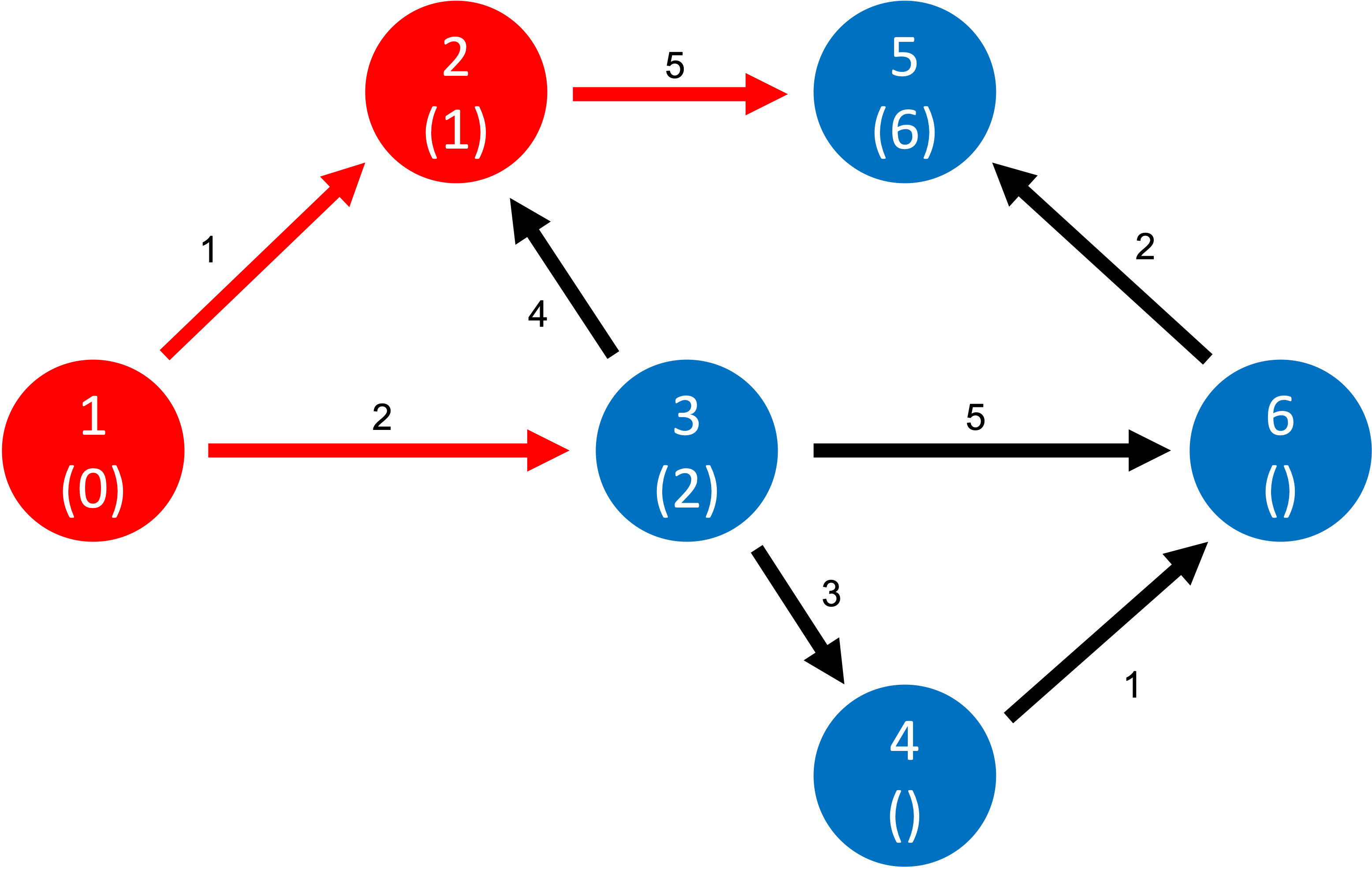
그럼 현재 1,2번 노드를 방문해서 빨간색으로 칠해놓겠습니다. 다음으로 최단거리값이 작은 노드는 무엇일까요?
맞습니다! 3번 노드가 가장 작죠.
3번 노드를 한번 봅시다. 3번노드는 2,4,6번노드를 방문할 수 있네요.
먼저 2번노드를 볼게요.
3번노드에서 2번노드로 가는 최단거리는 (3번까지최단거리 + 3번에서 2번사이의 가중치) = (2 + 4) = 6 이 됩니다!
그런데 2번노드는 현재 가지고있는 최단거리가 있으면서 1이네요.
그러면 갱신하지 않습니다.
이렇게 진행을 하면 다음과 같아지고, 다음에 오게되는 현재노드는 4번 노드가 되겠네요.
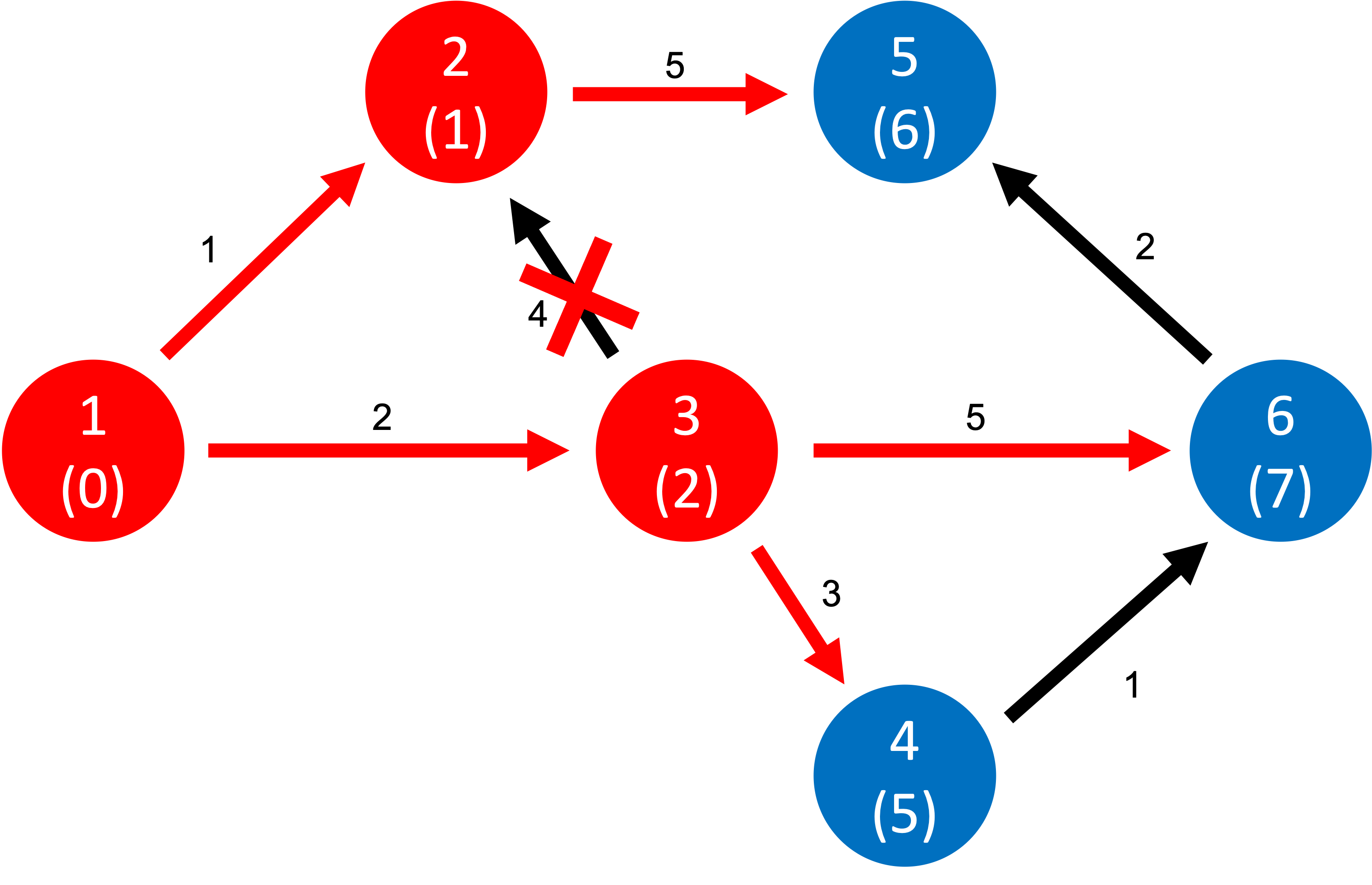
4번노드에서는 6번노드를 방문할 수 있고요, (6번의 현재 최단거리값)보다 (4번의 최단거리값 + 4번에서 6번사이의 가중치) 가 작으니 갱신하게 됩니다!
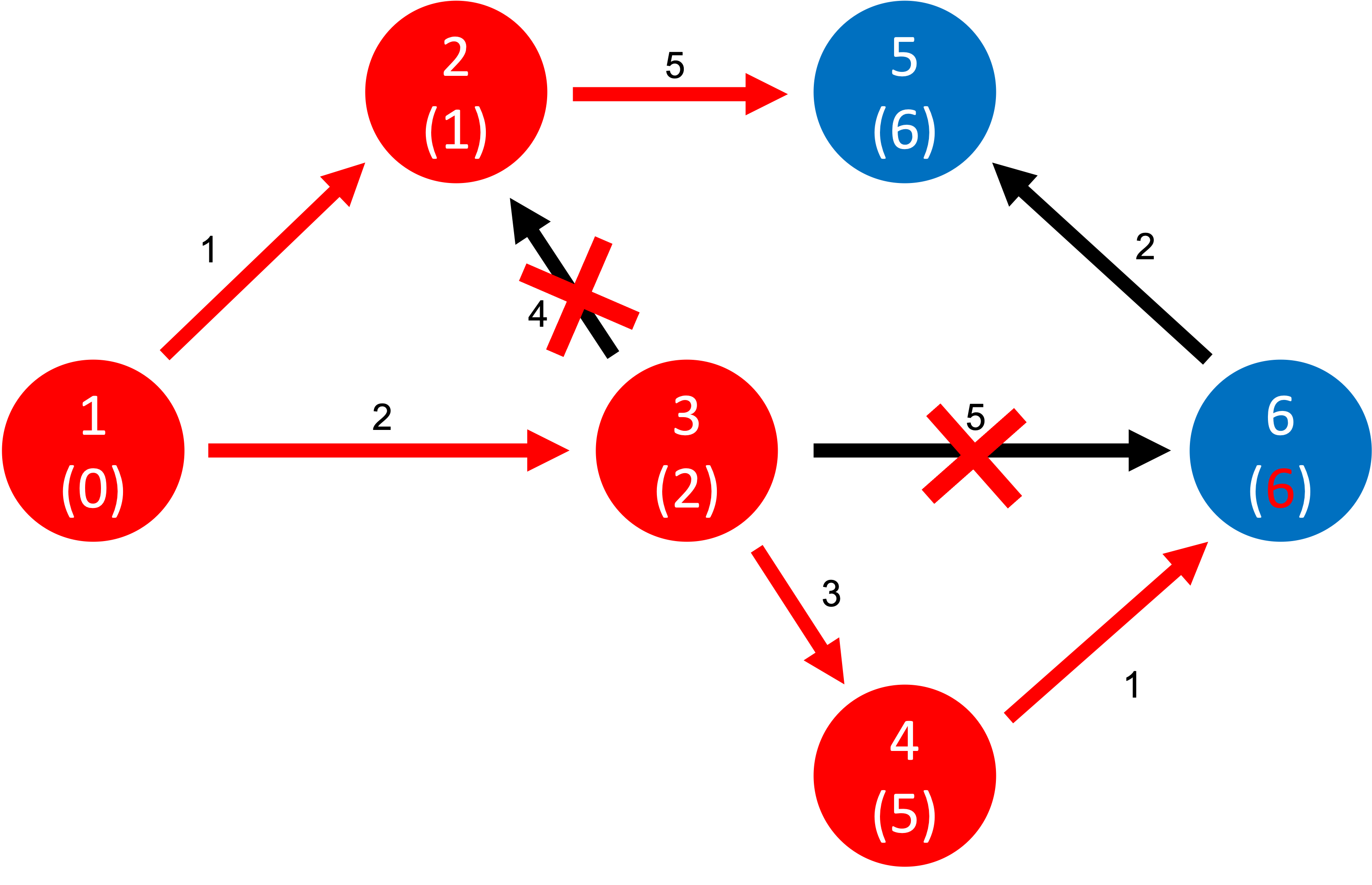
이제 이렇게 계속 모든 노드를 진행해 보시면 결과는 다음과 같아지게 됩니다!
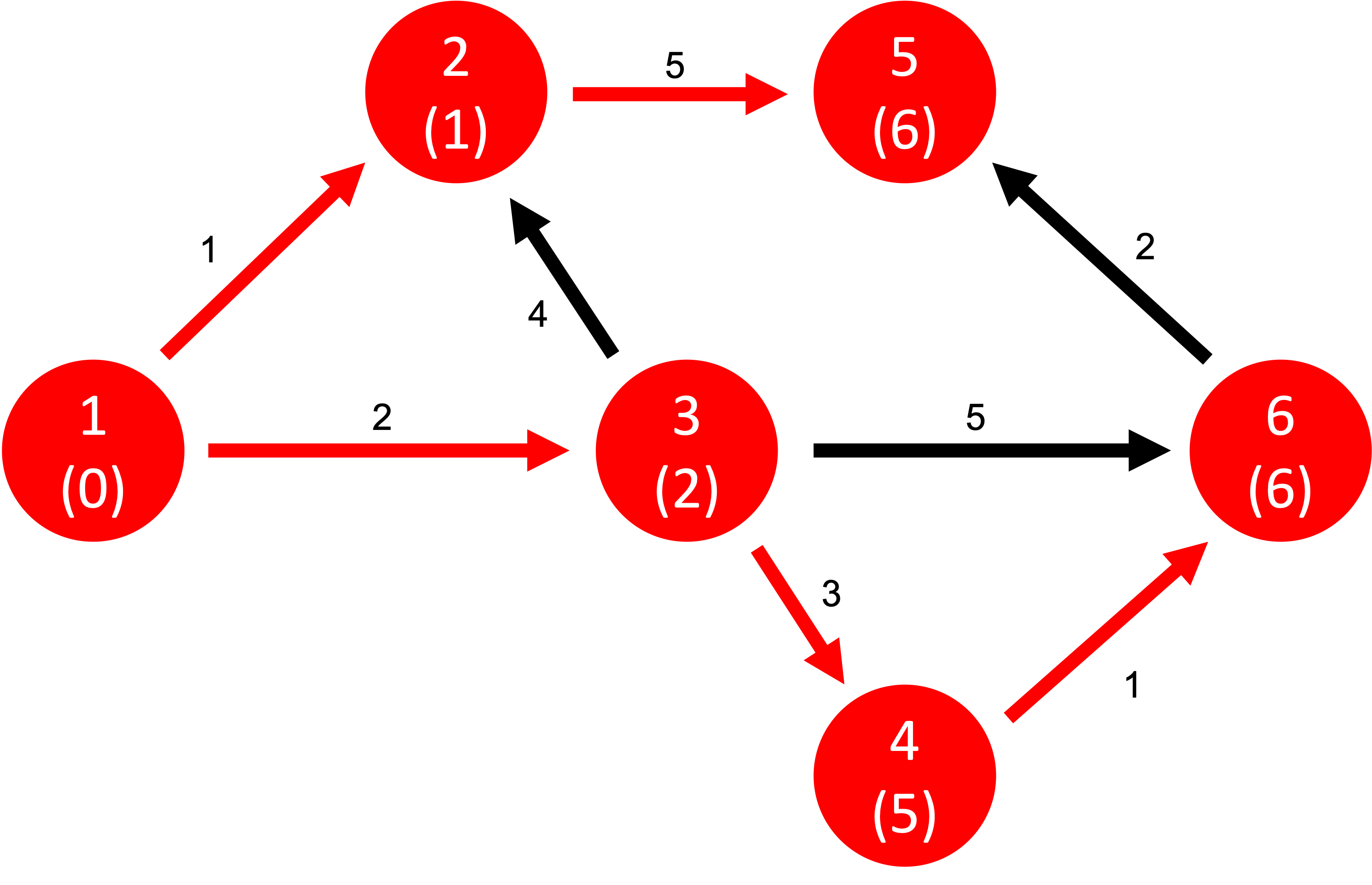
📌 필요한 자료구조
이제 컴퓨터적(?)으로 생각해봅시다!!!
필요한 자료구조는 무엇이 있을까요?
각 노드별로 최단거리를 저장해야하는데 어떤게 좋을까요? 저는 배열이면 충분할 것 같습니다.
int dist[n개의 노드];그리고 각 경로를 저장하고, 경로별 가중치를 저장해야하는데요. 이것은 어떻게 해결할 수 있을까요? c++이기 때문에 저는 <vector> 클래스를 이용할 예정입니다. vector에 배열형식으로 저장하여 선언할거에요.
vector< pair<int, int> > route[n개의 노드]이렇게말이죠!
마지막으로 가장 최단거리가 작은 값을 매 턴마다 뽑아낼 수 있어야 할 것입니다. 아무래도 우선순위 큐가 편할것 같네요.
#include <queue> //include 해주세요!
priority_queue <pair <int, int> > Data; 여기서 우선순위 큐에는 무엇을, 언제 넣어야 할까요?
최단거리를 갱신해야하는 경우입니다. 이 경우에 최단거리가 더 작아지기 때문에 갱신된 노드의 우선순위가 올라가겠죠??? 이때 갱신된 노드의 번호와, 해당 노드까지의 최단거리를 pair를 이용해 넣어주면 됩니다.
이렇게 선언하고 한번 위의 알고리즘을 구현해봅시다!
📌 핵심 알고리즘
다익스트라 알고리즘의 핵심은 아래 부분입니다. 사실 위의 원리만 이해하셨다면 아래부분은 세세하게 이해하실 필요보다는 문제를 풀면서 직접 구현해 보는 것을 추천드립니다!!
while (true) {
// 우선순위 큐가 비어있으면 break
if (pq.empty()) break;
Data now = pq.top();
pq.pop();
// 해당 노드에서 방문할 수 있는 노드를 탐색
for (int i = 0; i < v[now.node].size(); i++) {
Data next = v[now.node].at(i);
// 다음 노드의 최단거리값 > 현재노드의 최단거리갑 + 가중치 비교
if(dist[next.node] > dist[now.node] + next.weight){
dist[next.node] = dist[now.node] + next.weight;
// 최단거리를 갱신하는 경우 우선순위 큐에 다시 넣어줍시다!
pq.push(Data(next.node, dist[next.node]));
}
}
}