통계와 가까워지기 위해서
데이터 분석가를 꿈꾼다면 빠지지 않는게 바로 ’통계‘이다.
기초통계 강의도 듣고, 논문도 써봤지만 늘 통계는 어려웠다. 데이터 분석 프로젝트를 하면서는 그래프와 숫자로 장난질 하는게 이렇게 쉬웠다는걸(?) 새삼 깨닫고, 통계가 더욱 멀게만 느껴졌다.
그래서 이제는 지식으로서의 통계학을 배우는걸 넘어, 실제 통계가 무엇인지 익히고자 한다. 그 첫번째 시작으로 ’새빨간 거짓말, 통계‘ 책을 펼쳤다. 50년도 넘은 책이지만, 여전히 필독서로 꼽히는 책이라고 한다. 데이터리안의 ’데이터 넥스트 레벨 챌린지‘ 3기에 참가하여 다른 사람들과 함께 2주간 책을 읽기로 했다. 미뤄만 두던 책이지만, 데이터 분석에 관심있는 사람들과 같이 책을 읽고 의견을 나누기 때문에 더욱 책에 몰입하고 통계와 더 가까워지는 시간이 되리라 기대된다.
목차
PART 1. 언제나 의심스러운 여론조사
PART 2. 평균은 하나가 아니다
PART 3. 작은 숫자를 생략하여 사기 치는 법
통계의 함정
표본추출의 맹점
19쪽.
예일대학 졸업생들에 관한 기사는 표본에서 얻어진 것이다. 생존해 있는 1924년도 졸업생 모두를 추적할 수는 없으니 당연히 표본을 구성해야 한다.
졸업 후 상당한 시간이 지났으니 주소불명의 졸업생도 상당 수 있기 마련이다. 또 주소가 분명한 졸업생이라 하더라도, 대부분이 질문지에 회답하지 않는 것이 보통이고, 더구나 개인적인 사생활에 관한 질문지에 대해서는 더욱 더 그러하다.
“예일대학 졸업생의 연간 평균소득은 25,111달러이다!” 라는 말에 숨겨진 함정은 바로 ‘표본추출‘에 있다. 수십년이 지나 설문조사에 선뜻 응한 졸업생들이 과연 예일대 졸업생 전체를 대표한다고 말할 수 있을까?
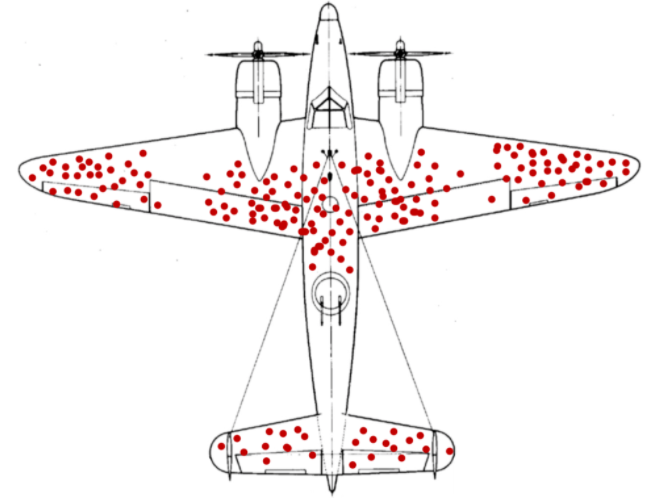
표본추출의 맹점과 관련한 또다른 사례로 2차 세계대전 전투기로 알아보는 ’생존자 편향‘이 있다.
당시에 전장에서 살아 돌아온 전투기의 총탄자국은 주로 날개와 꼬리에 집중되어 있었다. 이는 반대로 말하면, 살아 돌아온 전투기는 엔진과 조종석에 총탄을 맞지 않았기에 생존자가 될 수 있었다는 뜻이다. 즉 예일 대학 졸업생 중 설문조사에 응하지 않은 졸업생들 처럼, 돌아오지 못한 전투기들도 표본 추출 단계에서 표본에 포함되지 못한 것이다.
평균은 정말 대표할까?
52쪽
’연간 평균급여 1,368만 원‘이라고 할때 이 숫자는 엄청나게 높은 금액의 사장님 급여와 480만 원이라는 종업원의 급여 그 어느 쪽도 해당되지 않는 터무니없이 황당한 수치에 불과하다.
기술통계에서 대표값은 ‘평균’, ‘중앙값’, ‘최빈값’을 말한다. 가장 흔히 쓰이는 값은 평균이지만, 때론 아무런 정보도 주지 않곤 한다. 취업 준비를 위해 기업분석을 하다보면, 어느 기업은 평균 연봉이 얼마라더라, 하는 정보를 듣게 된다. 물론 대기업이고 유명한 기업일 수록 평균임금은 높고, 매우 부럽지만 신입사원 입장에서는 그다지 도움이 되지 않는 정보이다. 기업의 임금은 정규분포가 아니기 때문이다. 임금 뿐 아니라 다양한 사례에서 ’평균‘이 언제나 우리가 원하는 정보를 담고 있는 것은 아니기 때문에 항상 해석에 조심해야 한다.
구간으로 살펴보자
59쪽
1949년 미국 가정 한 세대의 평균소득이 3,100달러라는 신문기사가 있었다.
…
이 표를 다시 자세히 검토해보면, 이 추정치는 +-59달러의 오차범위 안에서 정확하다고 주장할 수 있는 확률이 19/20인 표본에서 추출된 값임을 알 수 있다.
이 문장이 무슨 뜻인지 단번에 이해하지 못해서 검색해서 95% 신뢰구간을 19/20으로 표현할 수 있다는 사실을 알게 되었다. 즉 평균 3,100달러는 95% 신뢰수준에서의 신뢰구간에서 오차범위 59달러일 때를 상정한 값인 것이다. 구간으로는 3,041~3,159달러로 나타낼 수 있다. 앞서 ‘평균’의 함정에 대해 말했지만, 이렇게 오차범위와 신뢰구간 등으로 추정치가 얼마나 신뢰할 수 있는지를 따질 수 있다.
대표적인 예로 선거철에 항상 등장하는 여론조사를 보면, A 후보가 B 후보를 오차범위 얼마 이내에서 얼마의 차이로 앞서고 있다고 말하곤 한다. 그러나 ’오차범위‘를 고려하면 차이가 역전되는 일이 심심찮게 벌어지곤 한다.
잠시 용어가 헷갈려서 정리해보자면,

표본오차 = 표집오차 = 오차한계 = 오차범위 = 최대허용오차
중심극한정리에 의해 모집단과 표본 통계량 사이의 표준편차을 ’표준오차‘ 라고 한다.
이 표준오차에 임계값을 곱한 값이 곧 ’표본오차‘ 이다.
따라서 표본오차는 신뢰수준에 따라 달라지게 된다.
표본의 크기
68쪽
어느 마을의 어린이 450명에게 이 백신을 접종하였고 동시에 접종을 하지 않은 680명 어린이의 통제집단을 구성하였다. 그 후 얼마 안 있어 이 유행병이 이 마을을 급습했는데 백신접종을 받은 아이들 중에서는 한 사람의 소아마비 환자도 생겨나지 않았다.
그런데 문제는 통제집단에서도 소아마비에 걸린 어린이가 한 사람도 없었다는 사실이다. 이 대규모의 실험을 행한 사람들은 소아마비의 감염률이 낮다는 사실을 모르거나 간과했던 것 같다. 소아마비의 일반적인 감염률에 따르면, 이 정도 크기의 집단에서 소아마비 환자가 발생할 기대값은 단 두 명뿐이다. 따라서 이 실험은 애초에 아무런 의미가 없었다. 무엇인가 의미 있는 결론을 얻기 위해서는 이 실험에서 다루었던 어린아이 수의 15배 내비 25배 정도의 표본이 필요했던 것이다.
이 구간에서 딱 떠오른 예는 화장품 광고였다. 피부 개선 효과를 입증하기 위해 실험했다는 설명 아래 자그마한 글씨로 ‘30대 여성 10명’ 이라고 적혀있다던가, 아예 통제집단 없이 실험집단만 존재한다던가 하는 사례를 화장품 광고에서 심심찮게 발견하곤 한다. 마치 극적으로 피부 개선 효과가 있는 듯이 표현했지만, 10명이 아니라 100명 1000명이었다면? 애초에 시간이 지나면 자연스레 개선되는 효과라면? 표본의 크기에 따라 값은 달라질 수 있고, 당연히 해석도 달라지게 된다.
평균만 보다가는..
86쪽
평균기온이 16도라 해도 기온의 분포 범위를 생각지 않고 결정하면 얼어 죽거나 아니면 타는 듯한 더위에 시달려야 할지도 모른다. 산 니콜라스의 기온은 8도에서 30도 범위 내에서 변화하지만 사막에서의 기온은 -9도에서 40도까지 변동하기 때문이다.
책을 읽으면서 가장 공감된 구절이었다. 얼마전 평균 기온만 보고 옷을 얇게 입었다가 밤에 추위에 떨었던게 생각이 났다. 특히 아침 저녁으로 기온차가 심한 환절기에는 날씨 검색 시 평균기온 뿐 아니라 최저 최고 기온이 몇도인지 살펴봐야할 이유가 이 구절로 설명이 된다.
파트 1~3까지는 크게 평균, 표본 두 개념의 함정에 대해서 다양한 사례와 함께 설명하고 있다. 책에 도표가 부족하긴 하지만 워낙 쉬운 예시들이라서 가볍게 읽으면서 이해하기 좋았다. 오히려 관련 용어를 까먹어서 다시 공부하느라 더 많은 시간을 쏟은 파트였다.
