알고리즘 - 너비 우선 탐색(BFS, Breadth-First Search)

탐색

그래프의 탐색은 하나의 정점에서 모든 정점을 방문하는 것을 의미한다.

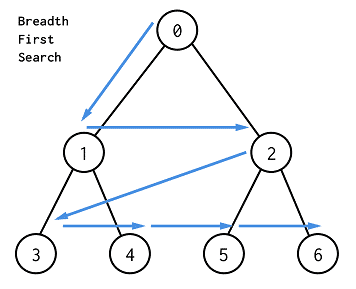
너비 우선 탐색

너비 우선 탐색은 노드에서 시작하여 인접한 노드를 먼저 탐색하는 것을 의미한다. 노드 사이의 최단 경로를 찾을 때 유리한 탐색 방법이다.

너비 우선 탐색의 특징

• 큐를 이용해서 구현한다.
• 재귀적으로 동작하지 않는다.
• 선입 선출 원칙으로 탐색

구현(JAVA)

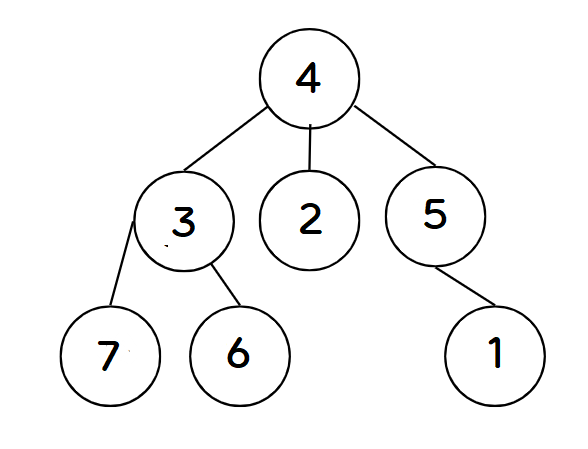
다음과 같은 그래프를 직접 BFS로 구현해보자

가장 상위 노드부터 시작한다고 가정했을 때, 방문한 노드는 큐에서 삭제해준다.
1. 먼저 방문할 최상위 노드를 큐에 넣는다. (4)
2. 4번을 방문하고 큐에서 뺀다. 이후 인접한 노드들을 큐에 넣는다. (2, 3, 5)
3. 3을 방문하고 이후 중복되지 않은 인접한 노드를 넣는다. (2, 5, 6, 7)
4. 2를 방문하고 중복되지 않은 인접 노드를 넣는다 (5, 6, 7)
5. 5를 방문하고 중복되지 않은 인접 노드를 넣는다 (1, 6, 7)
...
6. 모든 노드를 방문하면 종료한다.

	public static void main(String[] args) {
		int[][] graph = {{},{5},{4}, {4,6,7}, {2,3,5}, {1,4}, {3}, {3}};
		// 각 노드에 인접한 노드를 적는다.
		// 배열 인덱스를 노드와 매칭시키기 위해 인덱스 0은 비워둔다.
		
		boolean[] visited = new boolean[8];
		// 방문 처리용 boolean 배열
		
		System.out.println(bfs(4, graph, visited));
		
	}
	
	private static String bfs(int start, int[][] graph, boolean[] visited) {
		
		// BFS는 큐를 이용해 구현한다
		Queue<Integer> q = new LinkedList<Integer>();
		StringBuilder sb = new StringBuilder();
		// 시작 노드를 넣어준다.
		q.offer(start);
		  
		// 시작 노드는 방문 처리한다.
		visited[start] = true; 
		
		while(!q.isEmpty()) {
			int node = q.poll();
			sb.append(node + ",");
			// 큐에서 꺼낸 노드를 확인해준다.
			System.out.println(graph[node].length);
			for(int i = 0; i<graph[node].length; i++) {
				int temp = graph[node][i];
				
				if(!visited[temp]) {
					// 방문을 확인하고 방문하지 않았으면 큐에 추가
					visited[temp] = true;
					q.offer(temp);
				}
			}
		}
		// 탐색 순서 리턴
		return sb.toString();
		
	}


결과값
4->2->3->5->6->7->1->

참조