[자료구조] AVL 트리 정리

ego2·2023년 7월 30일

자료구조

AVL트리

모든 노드에 대해서 노드의 왼쪽 부트리와 오른쪽 부트리의 높이차가 1인 BST(이진탐색트리)
노드가 추가될 때, 삭제될 때 트리의 균형상태를 파악해서 스스로 구조를 변경해 균형을 잡는다.

높이 : 루트노드부터 단말 노드까지 가장 긴 하향 경로의 길이

AVL트리를 사용하는 이유

이진 탐색 트리의 평균 탐색 속도는 O(log N)이지만 한 쪽으로 치우쳐진 최악의 경우 탐색속도가 O(N)까지 저하 될 수 있다.

따라서 탐색을 효율적으로 하기위해 리밸런싱 작업을 통해 균형을 맞출 필요가 있다.

이진탐색 트리가 균형이 잡히면 h = O(log N)

💡 균형 잡힌 이진 탐색 트리를 유지하기위해 AVL트리를 활용함

AVL트리 조건

모든 노드에 대해 왼쪽 자식노드와 오른쪽 자식노드의 높이차가 최대 1이다.
높이 차이가 1보다 커지면 회전(Rotation)을 통해 균형을 맞춰준다.
삽입, 검색, 삭제 시간 복잡도 O(log N) 이다. (N : 노드의 갯수)

AVL트리 증명

N_h = N_{h-1}+ N_{h-2} + 1

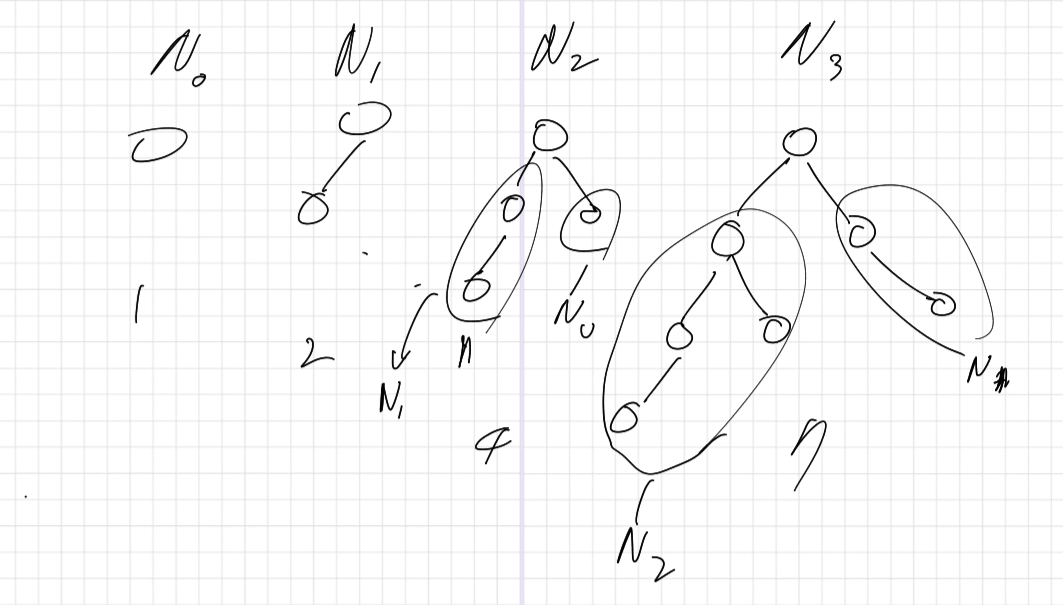
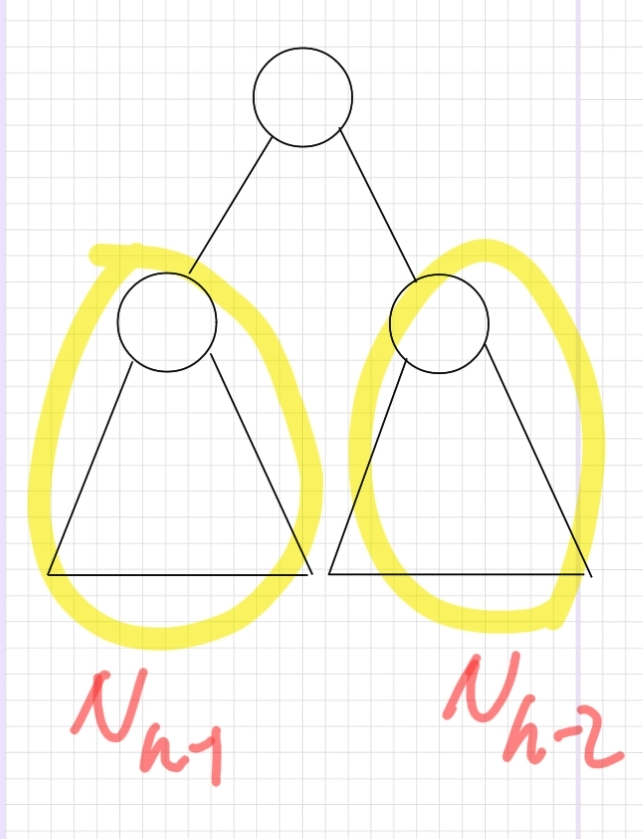
왼쪽 자식 노드 높이+ 오른쪽 자식 노드 높이+루트 노드

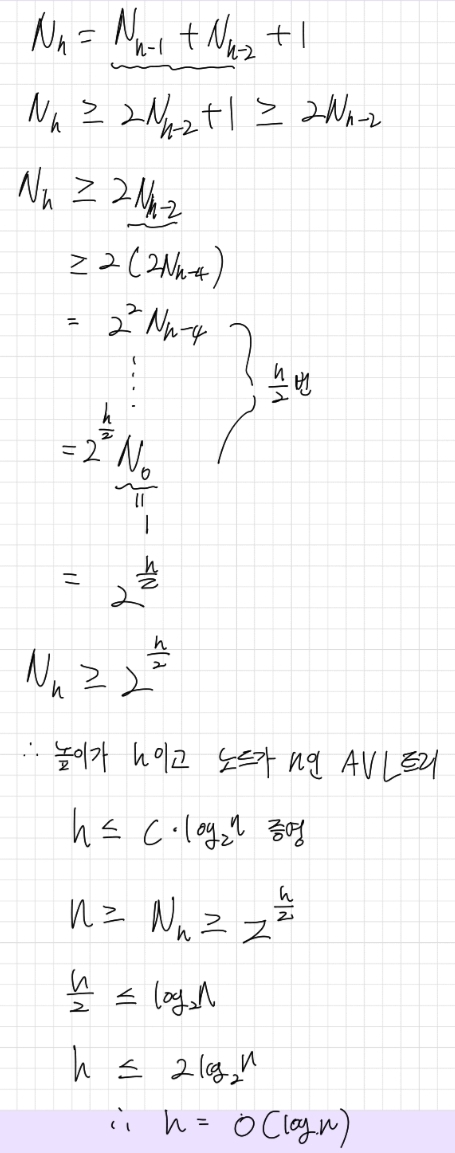
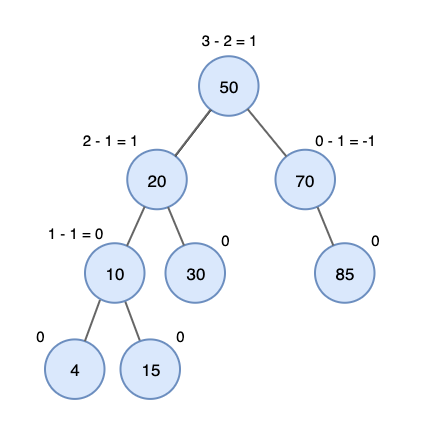
균형인수(Balance Factor, BF)

특정 노드의 왼쪽 서브트리의 높이에서 오른쪽 서브트리의 높이를 값 이다.

$BF = h_L-h_R$

각 노드의 BF값이 -1 or 0 or 1인 경우 균형이 잡힌 트리로 간주한다.

BF가 1이면 왼쪽 서브트리가 오른쪽 서브트리보다 높이가 한단계 높다는 것을 의미
BF가 0이면 왼쪽 서브트리와 오른쪽 서브트리의 높이가 같다는 것을 의미
BF가 -1이면 왼쪽 서브트리가 오른쪽 서브트리보다 높이가 한단계 낮다는 것을 의미

회전(Rotaion)

삽입 및 삭제 시 노드의 배열에 따라 4가지 타입(RR, LL, RL, LR) 불균형이 발생한다.
각 상황마다 Rotation을 통해 트리의 균형을 맞춘다.

4가지 타입(RR, LL, RL, LR)

새로 삽입된 노드 : N

가장 가까운 균형인수 +-2가 된 부모 노드 : A

RR 타입 : N이 A의 오른쪽 서브 트리의 오른쪽 서브 트리에 삽입된 경우(Right Right)
LL 타입 : N이 A의 왼쪽 서브 트리의 왼쪽 서브 트리에 삽입된 경우(Left Left)
RL 타입 : N이 A의 오른쪽 서브 트리의 왼쪽 서브 트리에 삽입된 경우(Right Left)
LR 타입 : N이 A의 왼쪽 서브 트리의 오른쪽 서브 트리에 삽입된 경우(Left Right)

Single Rotation

한번만 회전 시켜 균형 맞추는 것을 Signle Rotation이라고 함

RR회전

왼쪽으로 한번 회전하여 균형을 맞추게 된다.

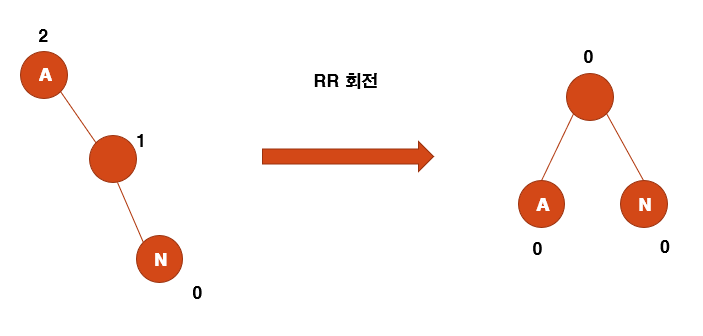
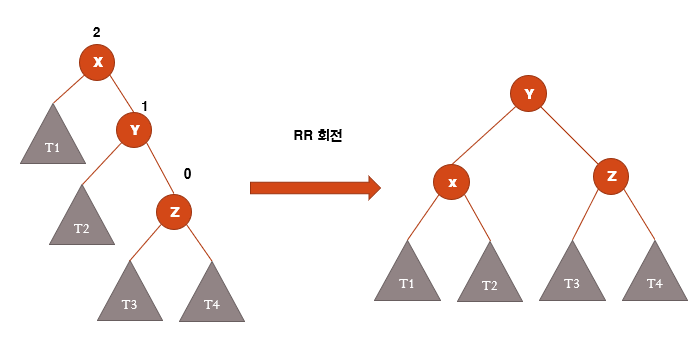
y노드의 왼쪽 자식노드를 x로 변경
x의 오른쪽 자식노드를 y의 왼쪽 서브트리(T2)로 변경
y를 루트로드로 변경

LL회전

오른쪽으로 한 번 회전하여 균형을 맞추게 된다.

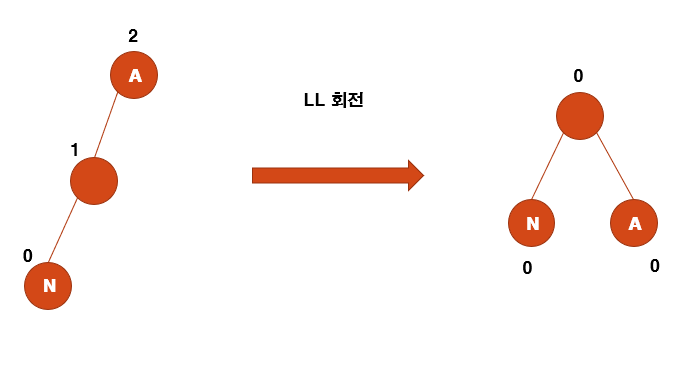
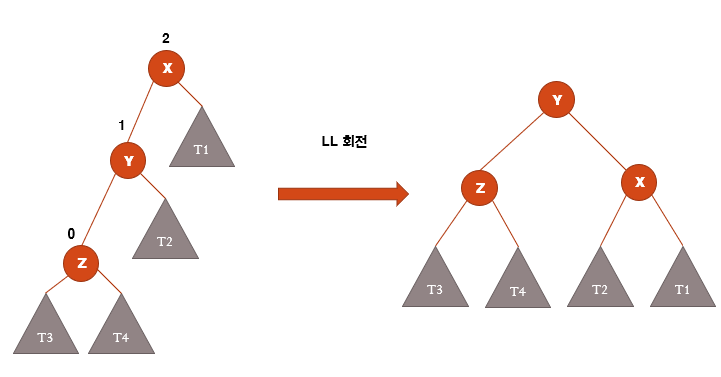
y노드의 오른쪽 자식노드를 x로 변경
x의 왼쪽 자식노드를 y의 오른쪽 서브트리(T2)로 변경
y를 루트로드로 변경

Double Rotation

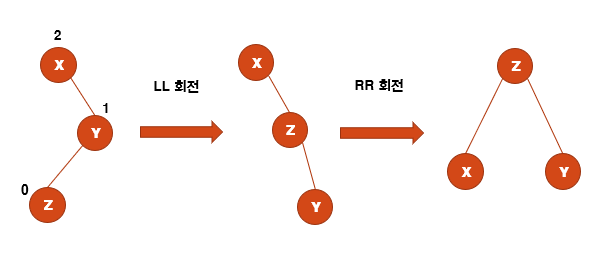
RL회전

RL회전을 균형 트리로 만들기 위해서 2번의 회전이 필요하다.

LL회전(오른쪽으로 회전)한 후, RR회전(왼쪽으로 회전)한다.

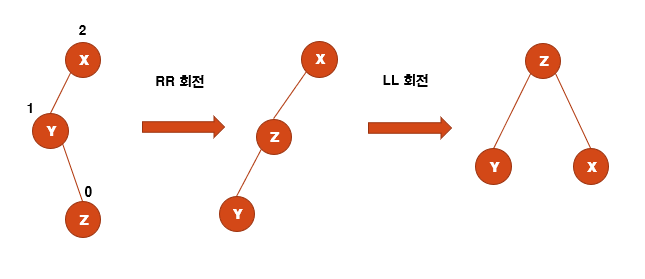
LR회전

RR회전(왼쪽으로 회전)한 후, LL회전(오른쪽으로 회전)한다.

삽입

균형을 이룬 이진 탐색 트리에서 균형상태가 깨지는 이유는 노드 삽입과 삭제 연산 때문에 발생한다.

노드 삽입으로 인해 불균형이 됐을 때 노드h(균형인수)가 -2 or +2가 된 가장 가까운 부모 노드의 서브 트리들에 대해 위에서 배운 회전을 통해 다시 균형을 잡아야 한다.

예제

[8, 9, 10, 2, 1, 5, 3, 6, 4]

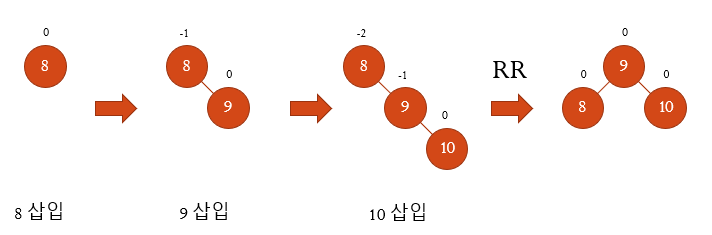
균형인수가 -2 or 2인 노드 중 최근에 입력한 노드와 가장 가까운 8을 기준으로 RR 회전한다.

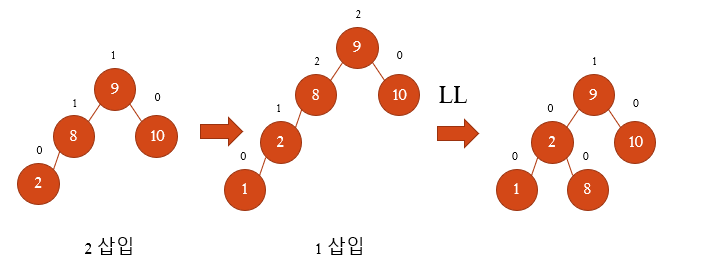
균형인수가 -2 or 2인 노드 중 최근에 입력한 노드와 가장 가까운 8을 기준으로 LL 회전한다.

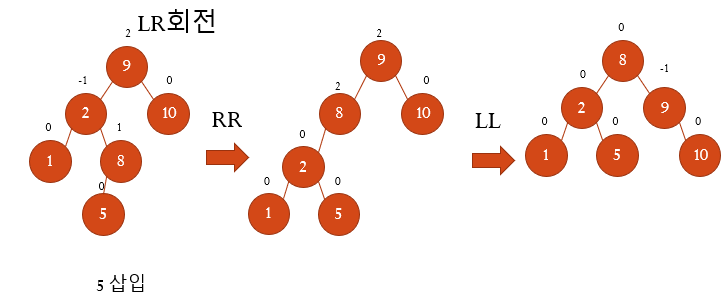
LR회전이므로 균형인수가 -2 or 2인 노드 중 최근에 입력한 노드와 가장 가까운 9기준으로 RR회전 후 LL회전을 한다.

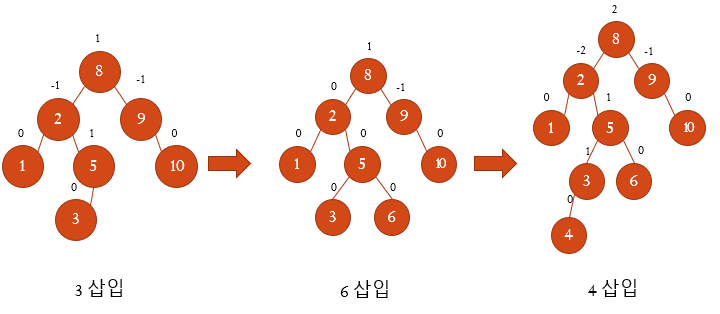
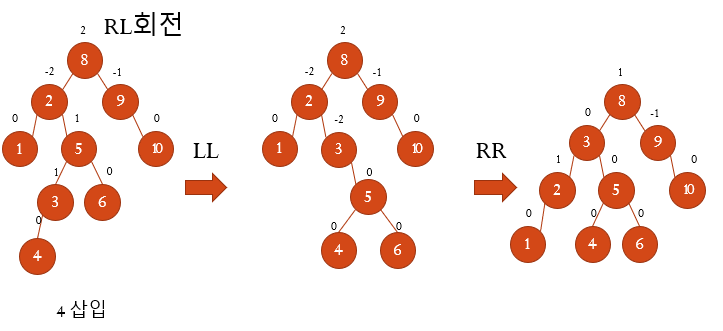
RL회전이므로 균형인수가 -2 or 2인 노드 중 최근에 입력한 노드와 가장 가까운 2기준으로 RR회전 후 LL회전을 한다.

삭제

왼쪽 부분 트리 중 최댓값을 갖는 노드나 오른쪽 부분 트리 중에서 최소값을 갖는 노드를 찾아 자리를 바꿔 삭제한다.

삭제 후 균형이 맞지 않는 경우 삽입과정과 마찬가지로 회전을 해준다.

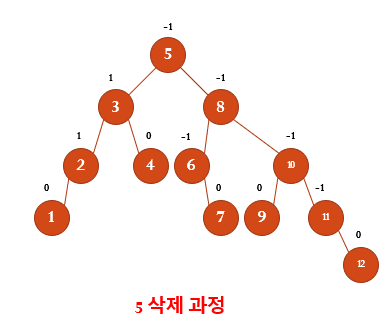
5와 왼쪽 부분 트리에서 가장 최대값을 가진 4와 바꾸고 삭제한다.

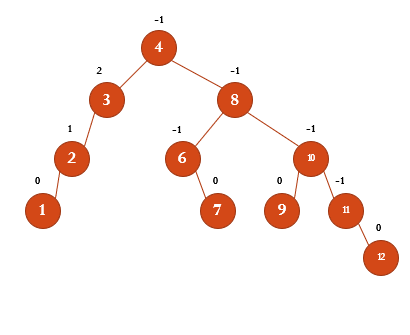
3에서 높이 차이가 2가 되기 때문에 LL회전을 통해 균형을 맞춰준다.

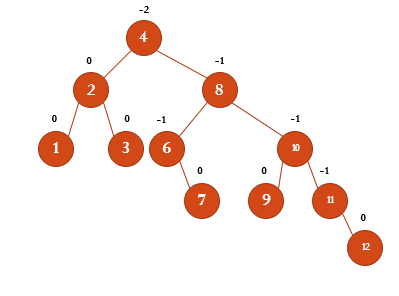
4에서 높이 차이가 -2가 되기 때문에 RR회전을 통해 균형을 맞춰준다.

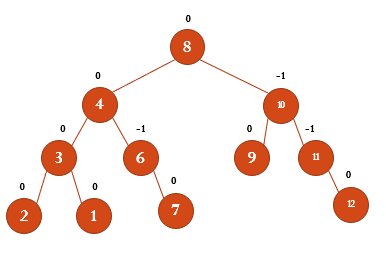
5삭제 완료

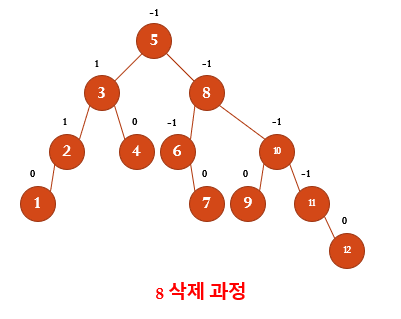
8을 왼쪽 부분 트리에서 가장 큰 수 7과 바꿔서 삭제한다.

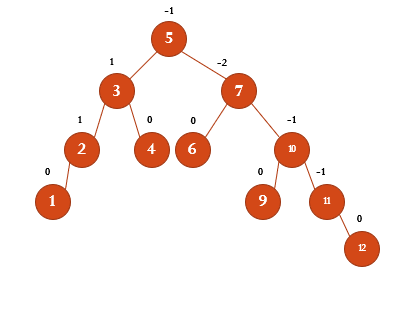
7에서 높이 차이가 -2가 되기 때문에 RR회전을 통해서 균형을 맞춰준다.

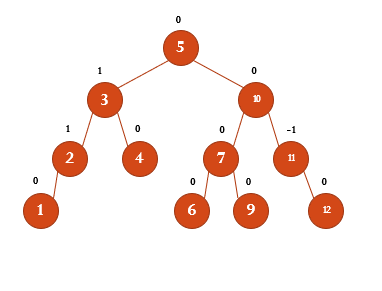
8삭제 완료

구현

#include <stdio.h>
#include <stdlib.h>

#define max(a, b) (((a)>(b))? (a) : (b))

typedef struct AvlNode
{
    int data;   //key값
    AvlNode *left_child, *right_child;

}AvlNode;

AvlNode *root;

//LL회전 (오른쪽으로 회전한다.)

//+-2를 가지는 A가 부모가 되고 A->left_child인 Brk child가 된다.
//1. A->left에 B가 가지고 있는 right_child를 대입하고 
//2. B의 right_child에 A를 대입

AvlNode* rotate_LL(AvlNode *parent)
{
    AvlNode *child = parent->left_child;
    parent->left_child = child->right_child;
    child->right_child = parent;
    return child;
}

//RR회전 (왼쪽으로 회전한다.)

//+-2를 가지는 A가 부모가 되고 A->right_child인 B가 child가 된다.
//A->right에 B가 가지고 있는 left_child를 대입하고 B의 left_child에 A를 대입

AvlNode* rotate_RR(AvlNode *parent)
{
    AvlNode *child = parent->right_child;
    parent->right_child = child->left_child;
    child->left_child->parent;
    return child;
}

//RL회전 (LL회전(오른쪽으로)=> RR회전(왼쪽으로))

//+-2를 가지는 A가 부모가 되고 A->right_child B가 child가 된다.
//A->right_child에 roate_LL(B)가 반환하는 값을 대입
//rotate_LL(B)호출시 B와 C가 변화가 생기고 다시 rotate_RR(A)을 호출하면 균형트리가 된다.

AvlNode* rotate_RL(AvlNode*parent)
{
    AvlNode *child = parent->right_child;
    parent->right_child = rotate_LL(child);
    return rotate_RR(parent);
}

//LR회전 (RR회전(왼쪽으로) => LL회전(오른쪽으로))

//+-2를 가지는 A가 부모 노드가 되고 A->left_child인 B가 child가 된다.
//A->left_child에 rotate_RR(B)가 반환하는 값을 대입한다.
//rotate_RR(B)호출시 B와 C가 변화가 생기고 다시 rotate_LL(A)을 호출하면 균형트리가 된다.

AvlNode* rotate_LR(AvlNode* parent)
{
    AvlNode *child = parent->left_child;    //B
    parent->left_child = rotate_RR(child);
    return rotate_RR(parent);
}

//트리의 높이 측정 함수
//재귀호출로 각각 높이를 구하고 이들 중에 더 큰값에 1을 더하면 트리의 높이가 된다.
int get_height(AvlNode *node)
{
    int height=0;
    if(node != NULL){
        height = 1+max(get_height(node->left_child), get_height(node->right_child));
    return height;
    }
}

//노드의 균형인수(BF) 반환 함수
//왼쪽 서브트리 높이 - 오른쪽 서브트리 높이
int get_balance(AvlNode* node)
{
    if(node == NULL) return 0;
    return get_height(node->left_child) - get_balance(node->right_child);
}

//균형 트리를 만드는 함수
AvlNode* balance_tree(AvlNode **node)
{
    int height_diff=get_balance(*node);

    if(height_diff > 1)        //왼쪽 서브트리의 균형을 맞춘다.
    {
        if(get_balance((*node)->left_child > 0)){
            *node = rotate_LL(*node); 
        }
        else{
            *node = rotate_LR(*node); 
        }
    }
}