세그먼트 트리

세그먼트 트리란?

여러 개의 데이터가 연속적으로 존재할 때, 특정한 범위의 데이터의 합을 가장 빠르고 간단하게 구할 수 있는 자료구조

예시 데이터 : 5 8 7 3 2 5 1 8 9 8 7 3
특정 구간 index 1~10 까지의 합을 구하는 방법?

방법 1. 단순 배열로 선형적으로 구하기

배열에서 위 범위를 하나씩 더하게 되면, 앞에서 하나씩 더해가므로 데이터의 개수가 N이면 시간 복잡도는 O(N)이 나오게 된다.

방법 2. 트리 구조를 이용해 구하기

1. 구간 합 트리 생성하기

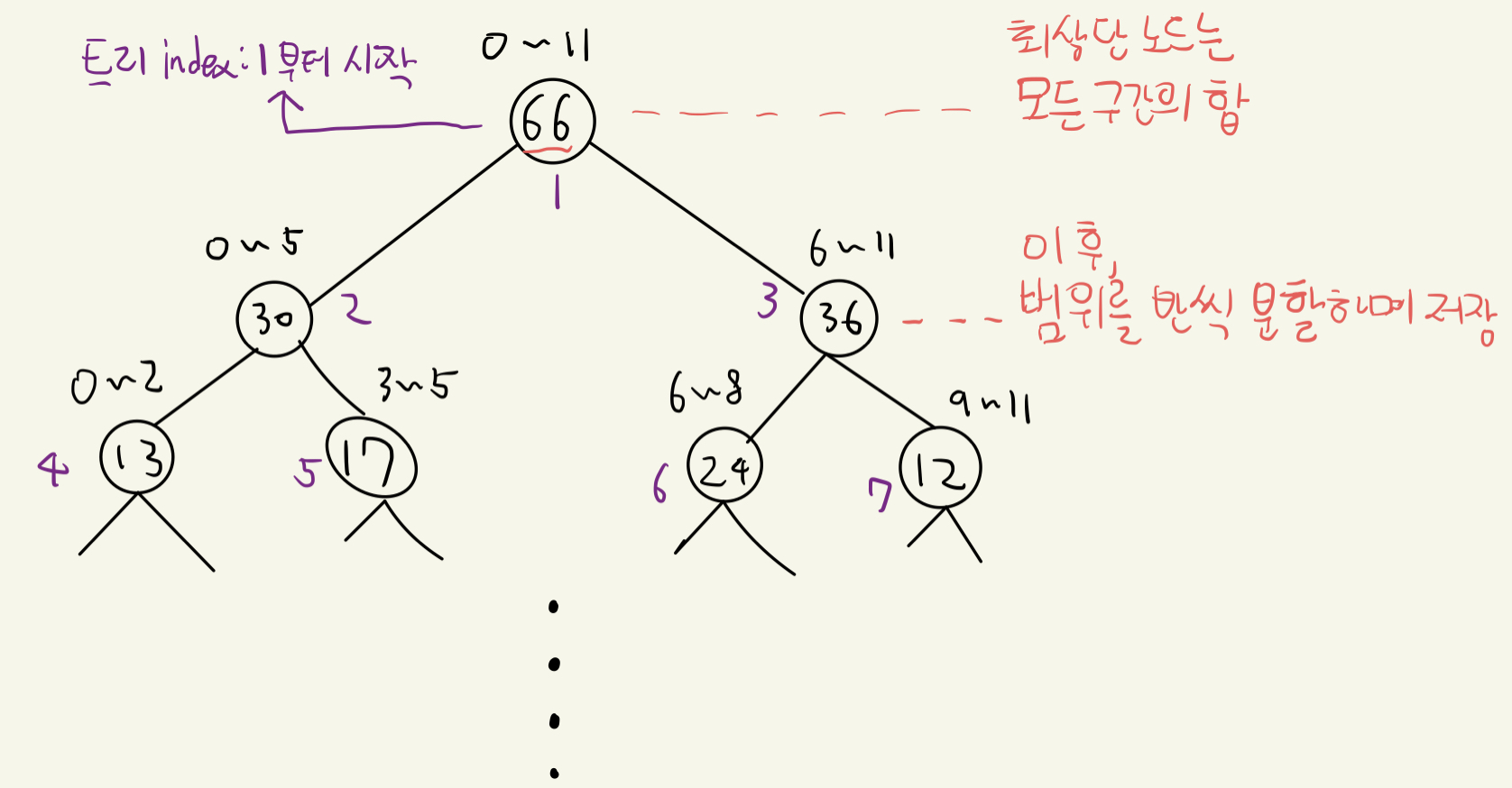
트리 index가 1부터 시작하는 이유는 2를 곱했을 때 왼쪽 자식 노드를 가리키게 되어 효과적이기 때문이다.

data = [5, 8, 7, 3, 2, 5, 1, 8, 9, 8, 7, 3]
tree = [-1] * 12 * 4	# 트리 사이즈를 미리 할당

def init(start, end, node):
  if start == end:
    tree[node] = data[start]
    return tree[node]
  mid = (start + end) // 2
  tree[node] = init(start, mid, node * 2) + init(mid+1, end, node * 2 + 1)
  return tree[node]

init(0, 11, 1)	# 시작 노드는 1

print(tree)
[-1, 66, 30, 36, 20, 10, 18, 18, 13, 7, 5, 5, 9, 9, 15, 3, 5, 8, -1, -1, 3, 2, -1, -1, 1, 8, -1, -1, 8, 7, -1, -1]

tree = [-1] * 32 # 트리의 사이즈를 (log N + 2) 만큼 미리 준비해야함
원래 세그먼트 트리의 크기는 크기가 N일때 N보다 큰 가장 가까운 제곱수를 구한뒤에 2배를 하여 구해야 하지만, 편하고 넉넉하게 하기 위하여 미리 N * 4(제곱수 포함)로 크기를 미리 할당해 놓는다.

2. 구간 합을 구하는 함수

구간 합은 트리 구조이기 때문에 항상 O(log N) 시간에 구할 수 있다. 트리를 내려가며 트리의 구간이 구하려는 구간의 범위 안에 있는 경우만 더해주게 되면 저절로 구간 합이 구해진다.

# left : 구하려는 구간의 왼쪽, right: 구하려는 구간의 오른쪽
def sum(start, end, node, left, right):
  # 범위 안에 있는 경우
  if start >= left and end <= right:
    return tree[node]
  # 범위 밖에 있는 경우
  if start > right or end < left:
    return 0
  # 둘다 아닌 경우(걸쳐 있음)
  mid = (start + end) // 2
  return sum(start, mid, node * 2, left, right) + sum(mid + 1, end, node * 2 + 1, left, right)

print(sum(0,11,1,4,8))	# index 4~8까지 구간합 구하기
25

3. 구간 합을 수정하는 함수 (특정 원소값 수정)

구간 합을 구하는 함수와 마찬가지로 해당 원소값을 포함하고 있는 구간 합 노드들만 갱신해 주면 된다.

def update(start, end, node, index, diff):
  if start == end:
    return;
  # 범위 밖인 경우
  if index > end or index < start:
    return;
  # 범위 안인 경우, 더 내려 가며 수정
  tree[node] += diff
  mid = (start + end) // 2
  update(start, mid, node * 2, index, diff)
  update(mid + 1, end, node * 2 + 1, index, diff)
  return;

update(0,11,1,7,1)
print(tree)
[-1, 67, 30, 37, 20, 10, 19, 18, 13, 7, 5, 5, 10, 9, 15, 3, 5, 8, -1, -1, 3, 2, -1, -1, 1, 8, -1, -1, 8, 7, -1, -1]

결론

세그먼트 트리를 이용하여 구간 합을 구하거나 수정할 때 O(log N)의 시간으로 빠르게 간편하게 처리할 수 있다.

전체 소스 코드

data = [5, 8, 7, 3, 2, 5, 1, 8, 9, 8, 7, 3]
tree = [-1] * 32

def init(start, end, node):
  if start == end:
    tree[node] = data[start]
    return tree[node]
  mid = (start + end) // 2
  tree[node] = init(start, mid, node * 2) + init(mid+1, end, node * 2 + 1)
  return tree[node]

# left : 구하려는 구간의 왼쪽, right: 구하려는 구간의 오른쪽
def sum(start, end, node, left, right):
  # 범위 안에 있는 경우
  if start >= left and end <= right:
    return tree[node]
  # 범위 밖에 있는 경우
  if start > right or end < left:
    return 0
  # 둘다 아닌 경우(걸쳐 있음)
  mid = (start + end) // 2
  return sum(start, mid, node * 2, left, right) + sum(mid + 1, end, node * 2 + 1, left, right)

def update(start, end, node, index, diff):
  if start == end:
    return;
  # 범위 밖인 경우
  if index > end or index < start:
    return;
  # 범위 안인 경우, 더 내려 가며 수정
  tree[node] += diff
  mid = (start + end) // 2
  update(start, mid, node * 2, index, diff)
  update(mid + 1, end, node * 2 + 1, index, diff)
  return;
  

init(0, 11, 1)

print(tree)
print(sum(0,11,1,4,8))
update(0,11,1,7,1)
print(tree)

Reference

https://m.blog.naver.com/ndb796/221282210534