다익스트라?

다익스트라 알고리즘은 한 지점에서 다른 특정 지점까지의 최단 경로를 구하는 알고리즘이다.

간선의 갯수를 E, 정점의 갯수를 V라 했을때,
한 정점의 가장 가까운 간선을 선택하는 과정에서 순차탐색이 아닌 우선순위 큐(heapq)를 쓴 다익스트라 알고리즘의 시간복잡도는 O(Elog V)이다.

과정

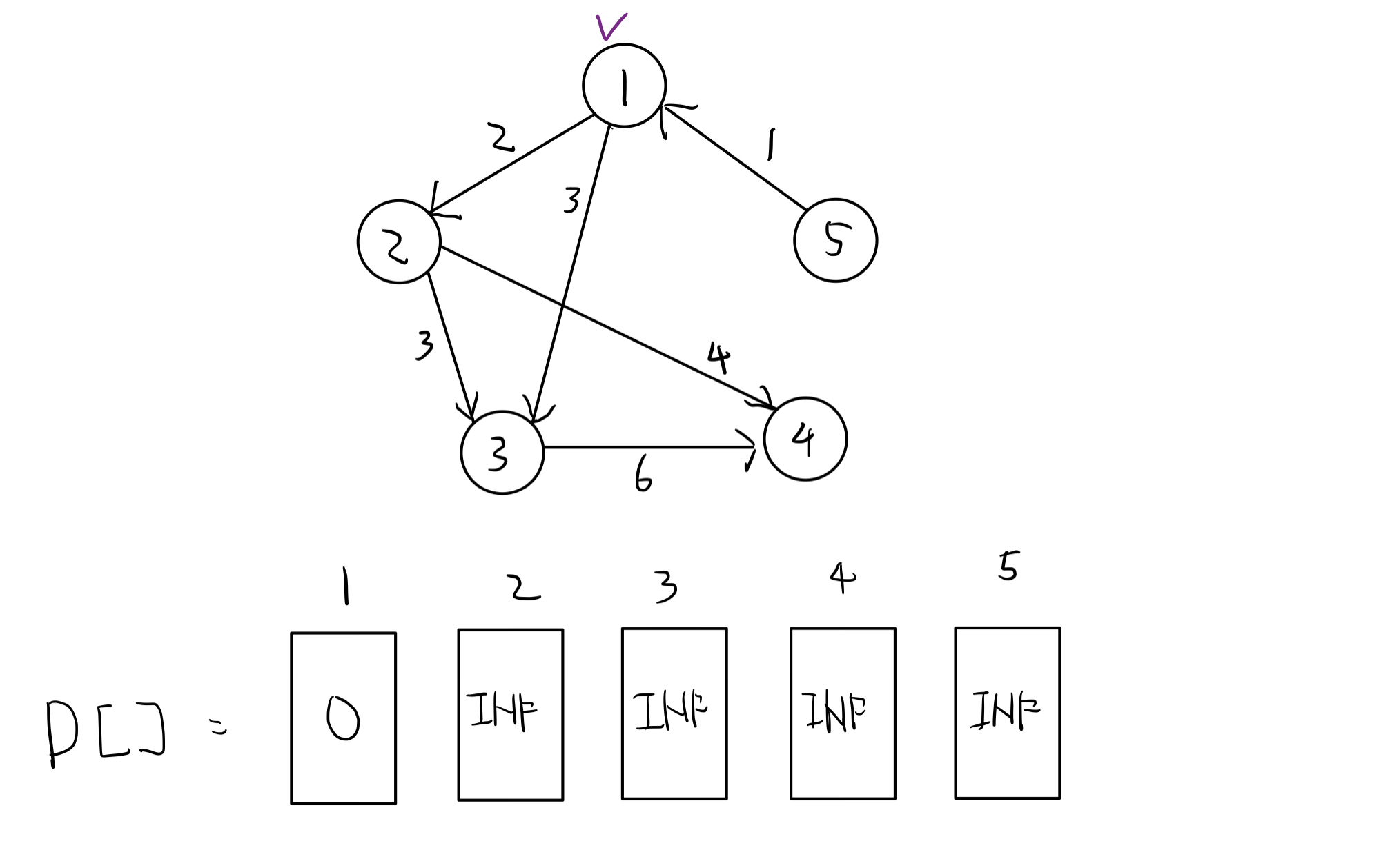
다음은 정점이 5개인 그래프의 초기 상황이다.
리스트 D는 정점 1에서 나머지 지점까지의 거리를 저장하고 있다.

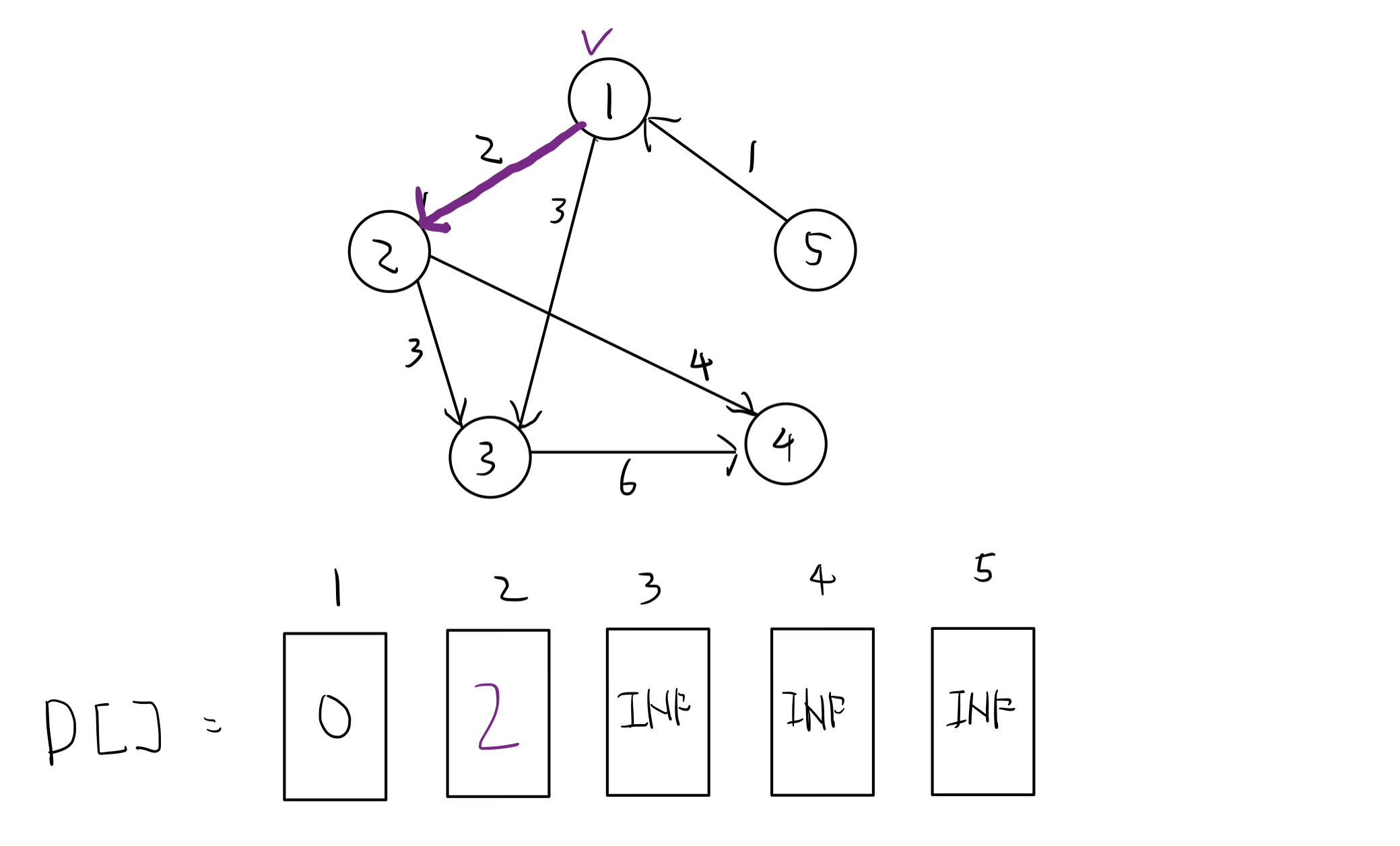
보라색으로 표시된 것은 현재 진행중인 정점/간선 이다.
정점 1의 간선들중 2로 가는 간선이 선택된 이유는 정점 1에서 가장 가까운 간선이기 때문이다.
현재까지 거리 + 다음 거리 < D에 저장된 최단 거리 ( 0 + 2 < INF ) 이므로, 리스트를 수정해준다.

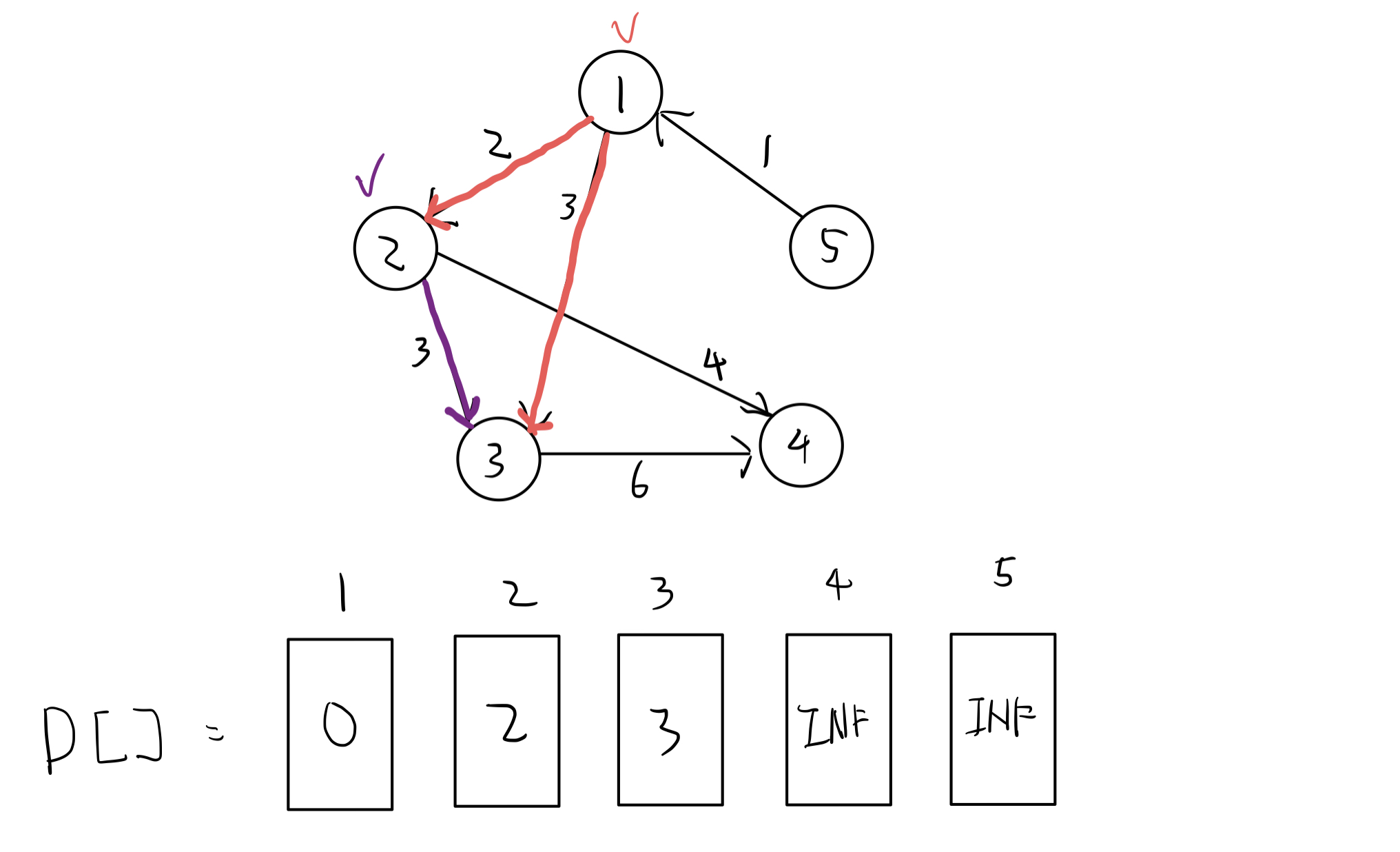
빨간색으로 표시된 것은 완료된 정점/간선 이다.
정점 2에서 3으로 갈때, 2 + 3 < 3 이므로 수정되지 않는다.

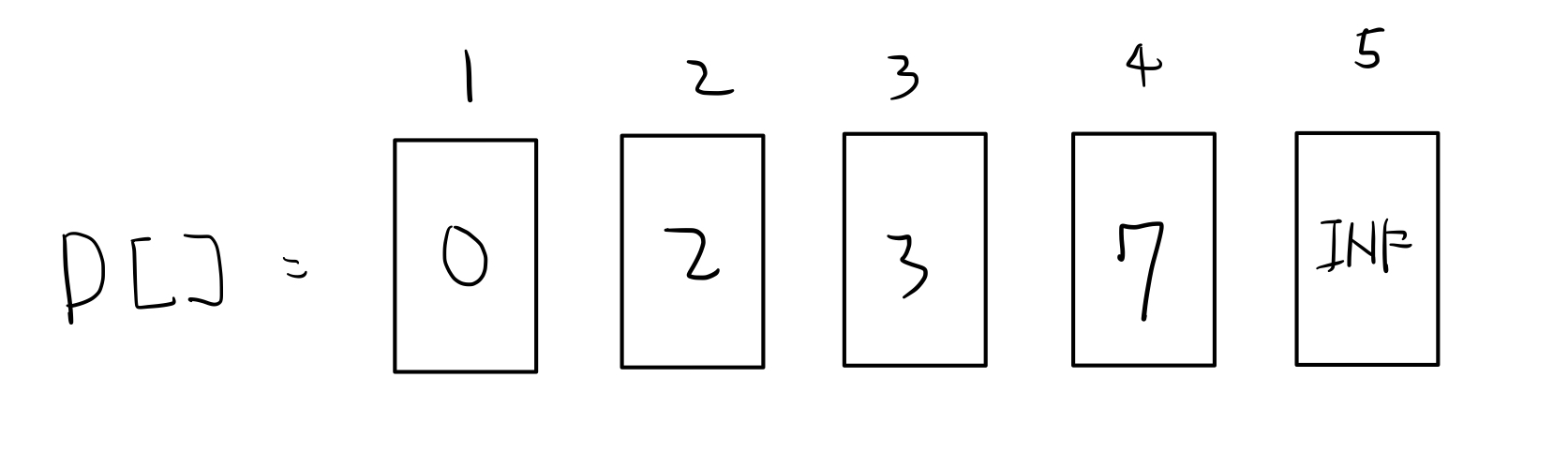
같은 방식으로 진행했을때 최종 결과이다.

구현 코드

import heapq

INF = int(1e9)

v, e = map(int,input().split())
start = int(input())

graph = [[] * (v+1)  for _ in range(v+1)]
distance = [INF] * (v+1)

for _ in range(e):
  a, b, c = map(int,input().split())
  graph[a].append((c, b))

def dijkstra(start):
  q = []
  distance[start] = 0
  
  heapq.heappush(q, (0, start))
  while q:
    now = heapq.heappop(q)
    nowDist, nowLoca = now[0], now[1]
    
    for node in graph[nowLoca]:
      nextDist, nextLoca = node[0], node[1]
      
      if distance[nextLoca] > nowDist + nextDist:
        distance[nextLoca] = nowDist + nextDist
        heapq.heappush(q, (nowDist + nextDist ,nextLoca))

dijkstra(start)